-

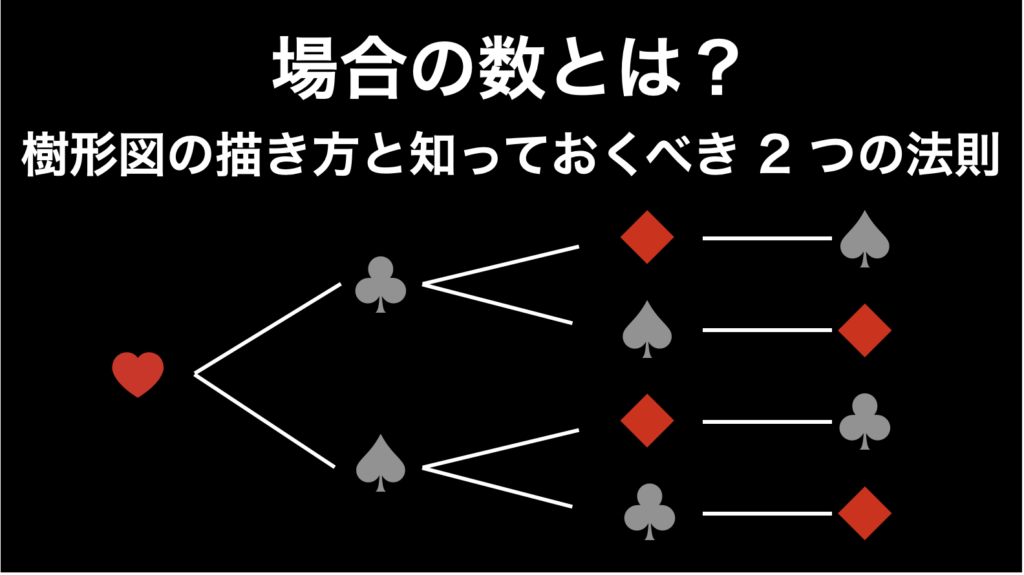
場合の数とは? 誰でも理解できるようにわかりやすく解説
場合の数は、確率について学ぶときに必ず出てくる言葉で、「ある特定の状況において起こりうる事象の数」を意味します。しかし「場合の数」という言い回しは直感的には意味が通らないため、多くの人がいまいち理解できずにいます。 そこで、このページでは... -

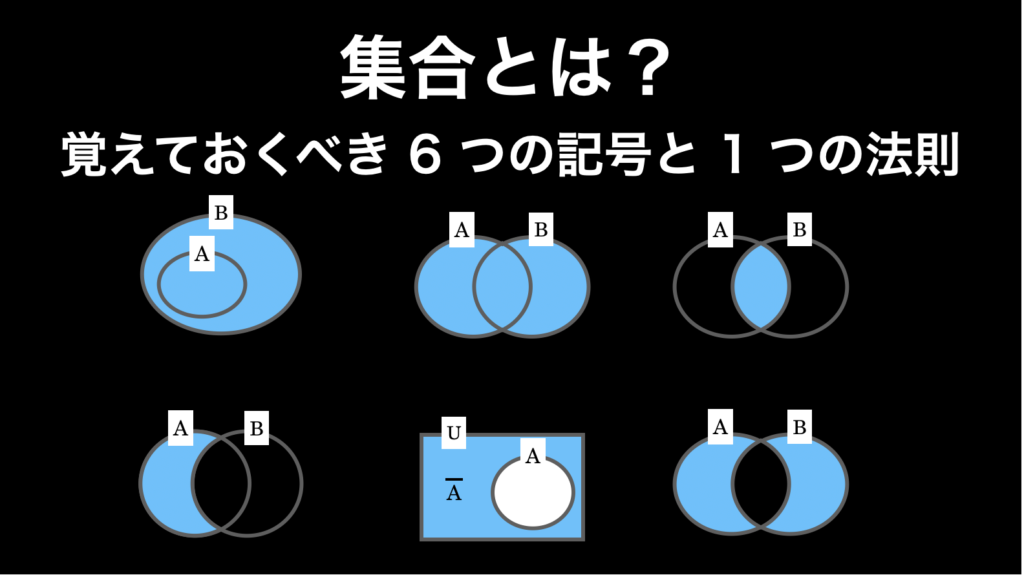
集合とは?覚えておくべき 6 つの記号と 1 つの法則
集合とは、簡単に言うと「何らかのモノが集まっているもの」のことです。これは集合論や確率論・論理学だけでなく、ほぼすべての数学分野で、非常によく使われます。なぜなら集合は、「数学の様々な演算をわかりやすく、やりやすくしてくれる非常に便利な... -

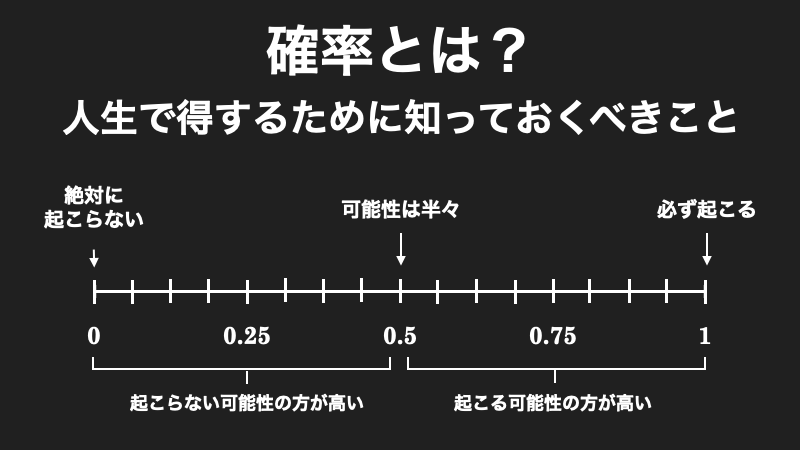
確率とは?知っておくと人生で得するかもしれない7つの知識
確率とは、「未来で良い思いをするために、現在ある選択肢の中で何を選ぶべきなのか」を教えてくれる数学の一分野です。 たとえば、スラム街の裏道を通ったら、強盗に襲われる確率が 90 % あるとしたら、あらかじめ、その道を通らないようにすることで、危... -

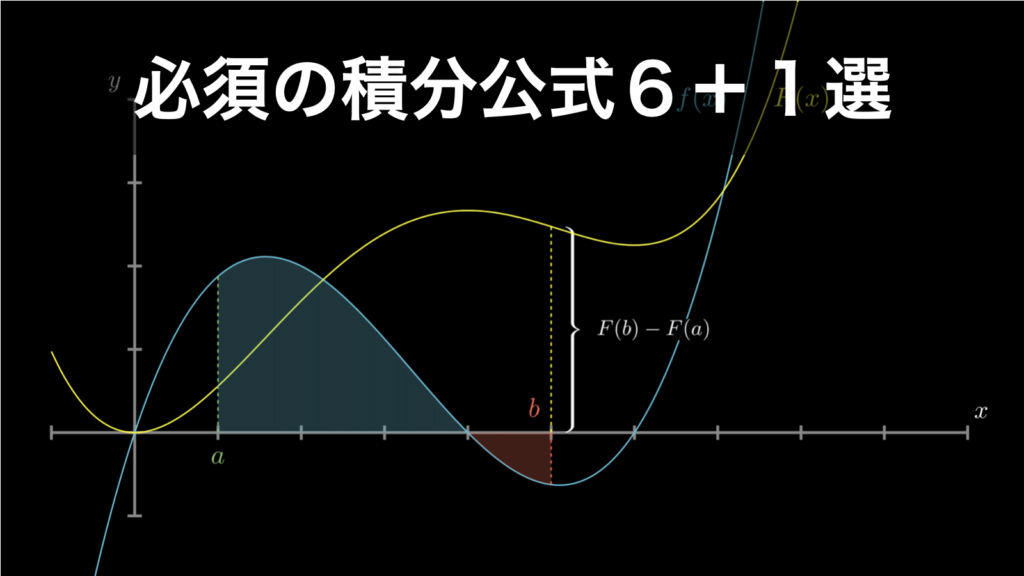
積分公式の一覧 ~ 知っておくべきもの6つ+1の解説 ~
当ページでは知っておくべき積分の公式を6+1つの合計7つ解説します。 プラス1となっているのは、最後の公式は、他の公式を理解していれば簡単に導き出すことができるため、必須ではないからです。しかし質問されることも多いため、ここに含めています... -

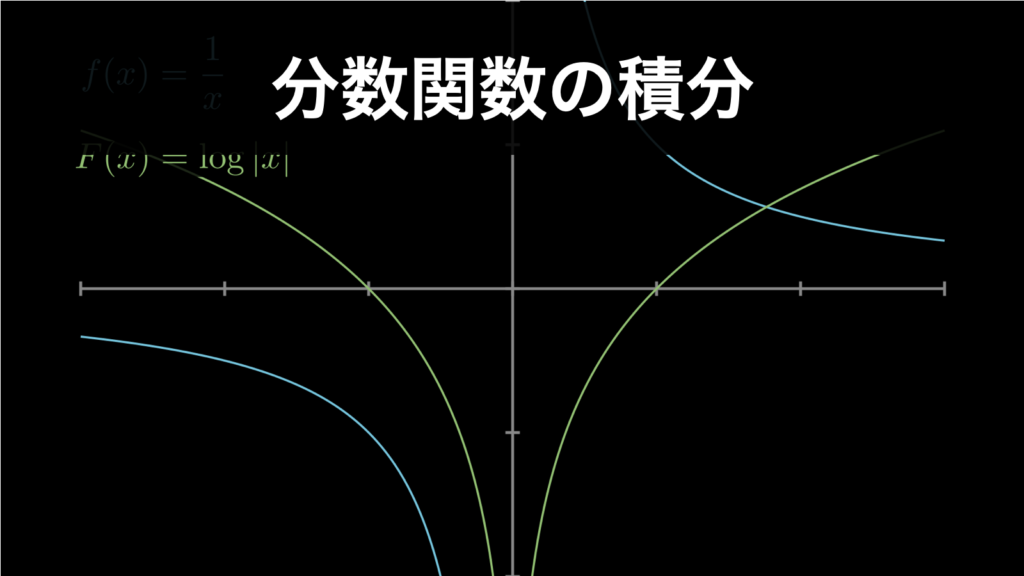
実は簡単!分数関数の積分のやり方と重要な2つのポイント
分数関数の積分は、何だか複雑なものに見えてしまうかもしれません。しかし、それは体系立てて解説しているものがほとんどないだけであって、本当は、ここまで一つずつ積分を学んできた方であれば、とても簡単に求めることができます。 なぜなら、置換積分... -

置換積分(合成関数の積分)のやり方と証明を誰でもわかるように解説
置換積分は、合成関数の積分を求めるために非常に役立つ公式であり、合成関数の微分と対になるものになっています。積分を行う上で必要なものなので、ここでしっかりと理解しておきましょう。 それでは早速始めたいと思います。 【1. 置換積分の公式】 置... -

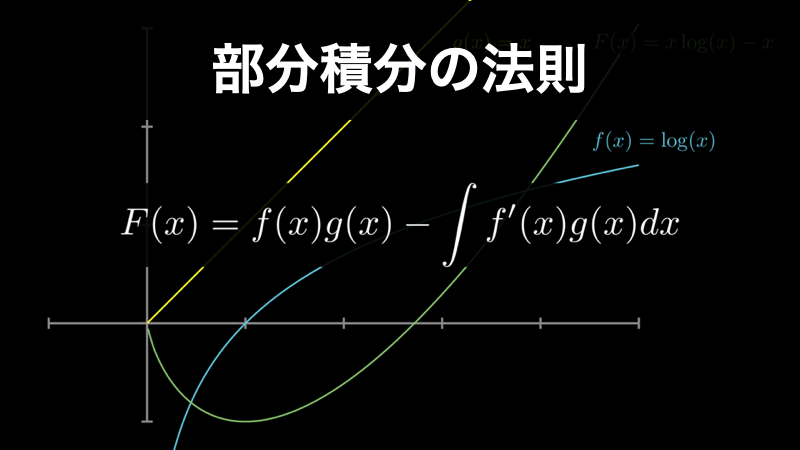
部分積分法 ~積(掛け算)の積分公式~ の使い方と解説
部分積分法は、関数の積を積分したいときに使う公式です。そして、積分は微分の逆演算であるため、部分積分法は積の微分公式の逆演算ということになります。 このページでは、この部分積分法について詳しく解説していきます。 【1. 部分積分法】 部分積分... -

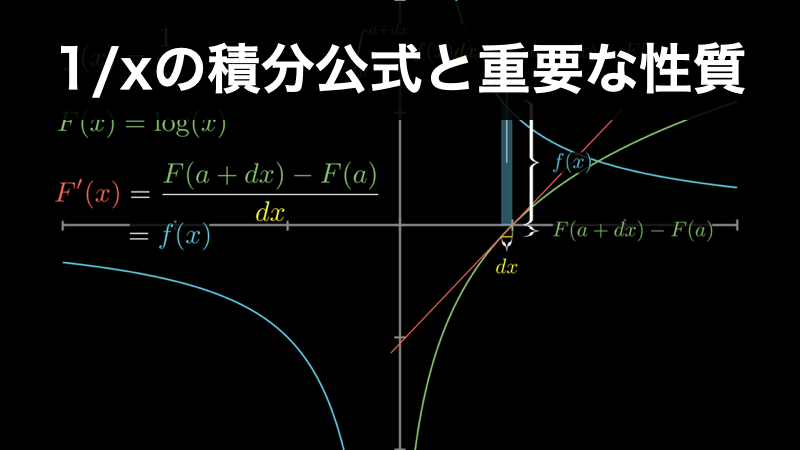
1/x の積分公式と知っておきたい面白い性質
関数 1/x は、微積分に重要な4つの関数(ベキ乗関数・三角関数・指数関数・対数関数)のうちのベキ乗関数に当たるものであり、現実世界の現象の中に特によく現れる関数(y=ax・y=x^2・ y=1/x・ y=sin x)の1つでもあります。 面白いものを挙げると、私た... -

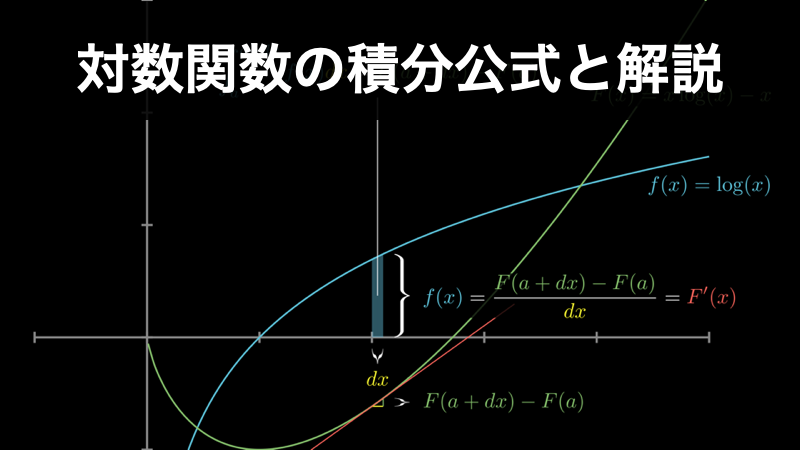
対数関数 log x の積分公式と2通りの証明の解説
対数関数は、微積分に重要な4つの関数(ベキ乗関数・三角関数・指数関数・対数関数)のうちの一つであり、例えば次のような自然現象に現れる関数です。 水素イオンの指数を示すpH騒音の程度を示すフォーン地震の強さを示すマグニチュード星の明るさを示す... -

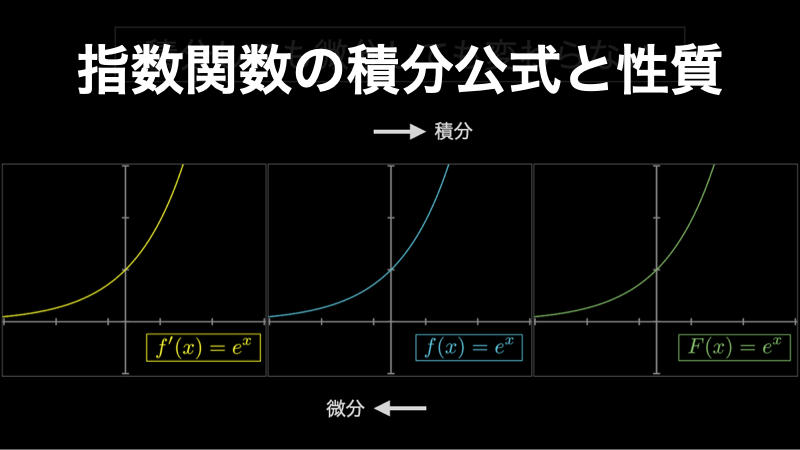
指数関数の積分公式と知っておくべき重要な2つの性質
指数関数は、微積分に重要な4つの関数(ベキ乗関数・三角関数・指数関数・対数関数)のうちの一つであり、複利金利・情報伝達・失敗情報の伝達(逆数)・蓮の葉の増殖・細胞分裂といった様々な現実世界の現象を表していることで有名です。 ここでは、この... -

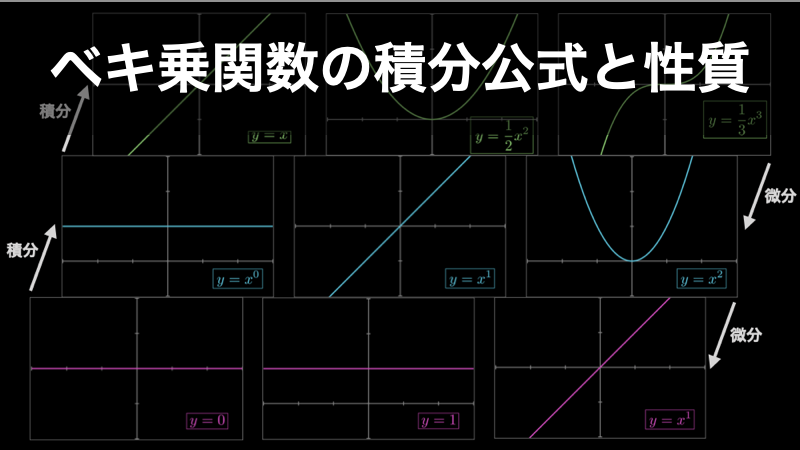
ベキ乗関数 x^2 の積分公式と抑えておきたい規則性
ベキ乗関数(特に y=x^2)は、基本中の基本の関数であり、現実世界のあらゆる現象に出てきます。例えば、放物線運動・焼肉の熱の通り具合・血圧と血管断面積の関係・ランチェスターの法則(戦力差モデル)などなど、実例を挙げようとすると枚挙にいとまが... -

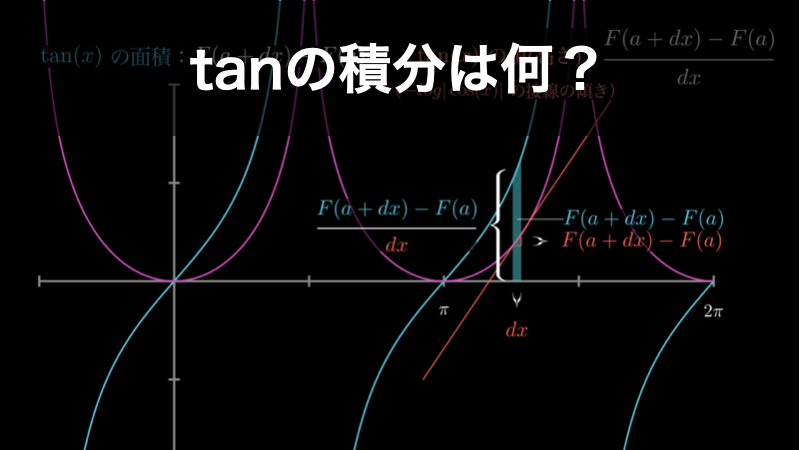
tanの積分は何?微積分の関係がよりよくわかるようになる解説
tan の積分は -log|cos(x)| になります。ここでは、なぜこうなるのかについて、イメージによって直感的に理解する方法と、数式によって理解する方法の2通りを解説します。 微積分に対する本質的な理解を得るための助けとなりますので、ぜひご覧頂ければと...