ベキ乗関数（特に y=x^2）は、基本中の基本の関数であり、現実世界のあらゆる現象に出てきます。例えば、放物線運動・焼肉の熱の通り具合・血圧と血管断面積の関係・ランチェスターの法則（戦力差モデル）などなど、実例を挙げようとすると枚挙にいとまがありません。
そのため、「現象のあるところに２次関数がある」と言っても過言ではないほどです。それぐらい、現実世界の現象を理解しようとすると、とにかく２次関数が現れます。
そのようなわけで、このページでは、この２次関数をはじめとしたベキ乗関数の積分について詳しく見ていきましょう。
1. ベキ乗関数の積分公式
\(x^2\) をはじめとするベキ乗関数の積分は、次の公式で求められます。
ベキ乗関数の不定積分
\[\begin{eqnarray}
\int x^ndx
=
\frac{1}{n+1}x^{n+1}
\end{eqnarray}\]
例えば \(x^2\) の積分は以下の通りです。
\[\begin{eqnarray}
\int x^2dx&=&\frac{1}{2+1}x^{2+1}\\
&=&\frac{1}{3}x^3
\end{eqnarray}\]
ベキ指数が自然数以外の場合でも変わりません。例えば \(x^{\frac{1}{2}}\) の積分は次のようになります。
\[\begin{eqnarray}
\int x^{\frac{1}{2}}dx&=&\frac{1}{\frac{1}{2}+1}x^{\frac{1}{2}+1}\\
&=&\frac{2}{3}x^{\frac{3}{2}}\\
&=&\frac{2}{3}\sqrt{x^3}
\end{eqnarray}\]
他にも、よく目にするベキ乗関数の積分を確認してみましょう。
よく目にするベキ乗関数の積分
\[
\begin{array}{ccc}
F(x): & -\dfrac{1}{2}x^{-2} & -x^{-1}& \log x & \ \ x \ \ & \ \ \dfrac{1}{2}x^2 \ \ & \ \ \dfrac{1}{3}x^3 \ \ \\
& \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow\\
f(x): & x^{-3} & x^{-2} & x^{-1} & x^0 & x^1 & x^2\\
\end{array}
\]
このうち \(x^{-1}(=\frac{1}{x})\) の積分は例外です。これを、積分公式を使って解こうとすると、分母が \(0\) になるため計算不可能なのですが、実際には \(\log x\) になります。この点については、また後で解説します。
さて、単に試験問題を解くことが目的であれば、これらを暗記しておけば十分です。しかし公式を暗記して試験問題を解けたとしても、それは数学パズルを解くことが得意になるだけであって、数学を理解しているということにはなりません。そのため、現実世界の問題解決に応用するための地頭を鍛えることにはなりません。
そこで、ここからは、このベキ乗関数の積分について、より深く考えていくことにしましょう。
2. ベキ乗関数の幾何学的解説
まずは、上の公式の意味を幾何学的に考えてみましょう。数学を幾何学的に考えるのは、数学を数式で考えるのと同じくとても重要なことです。幾何学的に考えることで数式の理解が深まりますし、反対に数式を理解することで幾何学的な理解も深まるようになっているのです。
なお、微積分の幾何学を理解する上で、まだ『べき乗（累乗）の微分公式を誰でも必ず深く理解できるように解説』を読んでない方は、ぜひ、先にそちらをご確認頂ければと思います。
それでは、おさらいとして微分公式を思い出してみましょう。まず、\((x^2)^{\prime}=2x\) の係数 \(2\) は面積の増し分に寄与する長方形の数のことでしたし、\((x^3)^{\prime}=3x^2\) の係数 \(3\) は体積の増し分に寄与する立方体の数のことでした。つまり微分公式における係数は増し分 \(dy\) に寄与する部分の数であるということです。
さて、本題である積分公式の係数部分 \(\frac{1}{n+1}\) は何を意味するのでしょうか。
まずは関数 \(f(x)=x\) で考えてみましょう。\(\int xdx=\frac{1}{2}x^2\) です。下図で視覚的に見てみると、この係数 \(\frac{1}{2}\) は、「一辺の長さが \(x\) の正方形の面積 \(x^2\) を半分にする」ためのものであることがわかります。
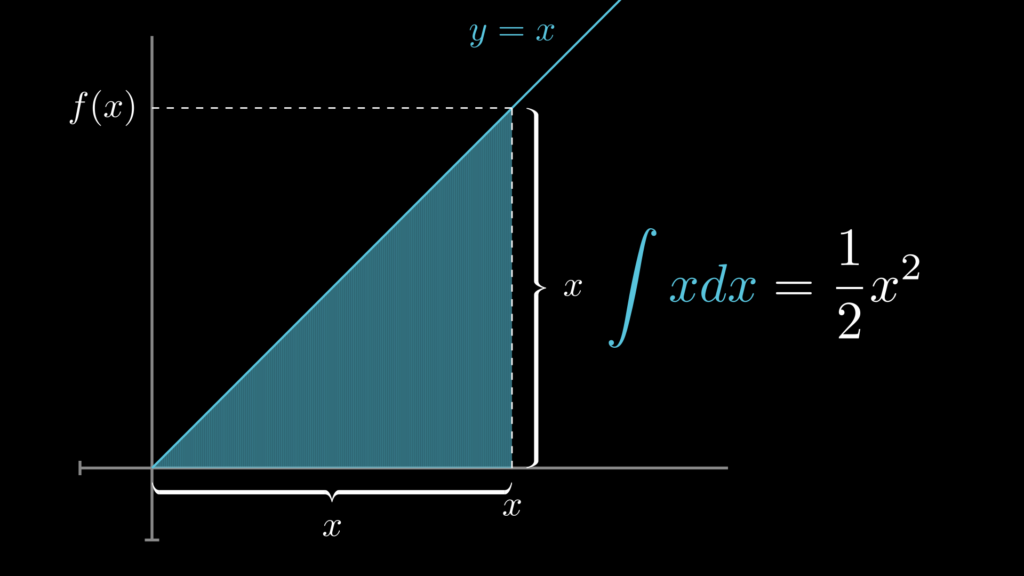
同じように、\(\int x^2dx=\frac{1}{3}x^3\) の係数 \(\frac{1}{3}\) は、「一辺の長さが \(x\) の立方体の体積 \(x^3\) を３分割にする」ためのものです。そして、\(\int x^3dx=\frac{1}{4}x^4\) の係数 \(\frac{1}{4}\) は「一辺の長さが \(x\) の四次元体の総量体 \(x^4\) を４分割にする」ためのものです。
つまり、\(\int x^ndx\) という積分は、幾何学的には「一辺の長さが \(x\) の 『\(n+1\) 次元体』を『\(n+1\)分割』したもの」を意味するものなのです。このことから積分公式の係数 \(\frac{1}{n+1}\) は、その分割数を示す数であることがわかります。
これで、なぜ、ベキ乗関数の積分公式が導き出されるのかが分かりましたね。続いて、これをさらに別の視点である「規則性」という観点から眺めてみましょう。
3. ベキ乗関数の微積分の規則性
ベキ乗関数の微積分には、面白い性質があります。それは、以下のように微分・積分を並べると、係数の部分もベキ指数の部分も１つずつ左から右にスライドしていくという規則性です。
ベキ乗関数の微積分の規則性
\[
\begin{array}{ccc}
F(x): & -\dfrac{1}{2}x^{-2} & -x^{-1}& \log x & \ \ x \ \ & \ \ \dfrac{1}{2}x^2 \ \ & \ \ \dfrac{1}{3}x^3 \ \ \\
& \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow\\
f(x): & x^{-3} & x^{-2} & x^{-1} & x^0 & x^1 & x^2\\
& \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow\\
f^{\prime}(x): & -3x^{-4} & -2x^{-3} & -x^{-2} & 0 & 1 & 2x^1
\end{array}
\]
\(y=x^{-1}\) の積分と、\(y=x^0\) の微分を除いて、この性質はベキ指数がどれだけ小さくなろうとも大きくなろうとも変わりません。また、ベキ指数が整数でなくても変わりません。常に規則正しく変化していきます。ぜひ実際に求めて確認してみてください。
3.1. ベキ乗関数の微積分を視覚的に確認
この「規則性」について、視覚的にも確認してみると面白いことがわかります。具体的には、以下のようになっています。
- ベキ指数が正の数の場合、積分は、以下の図を１つずつ右にズラしたものになる（微分は１つずつ左にズラしたものになる）。
- ベキ指数が−２以下の場合、微分しても積分しても、グラフの形が反転する。
まず一つ目の点から見てみましょう。以下の画像をご確認ください。
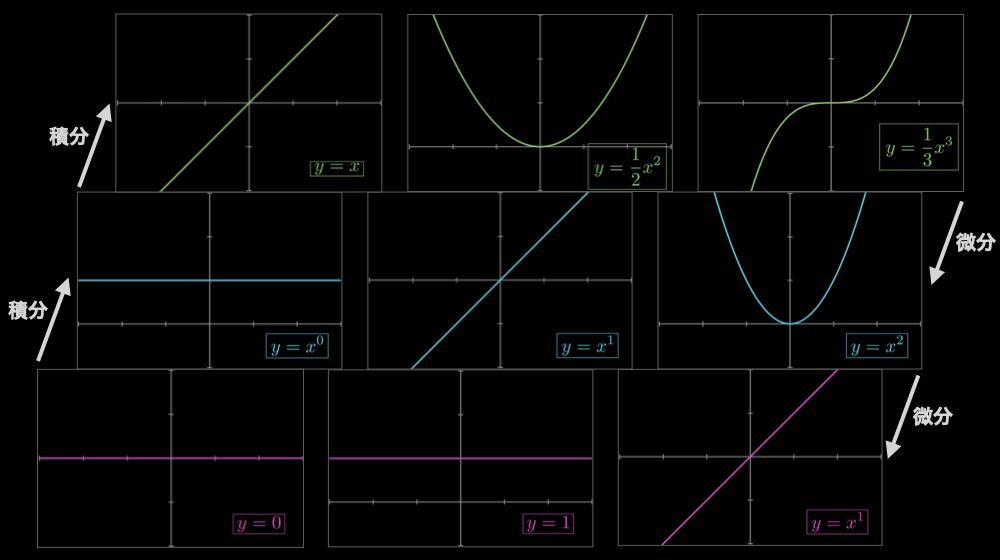
このように、ベキ指数が正の数の場合、積分をすると、グラフの形は右にズレていくようになっています。この性質は、ベキ指数がどれだけ大きくなっても変わりません。これが一つ目の規則性です。
次に二つ目の点を見てみましょう。以下の画像をご確認ください。
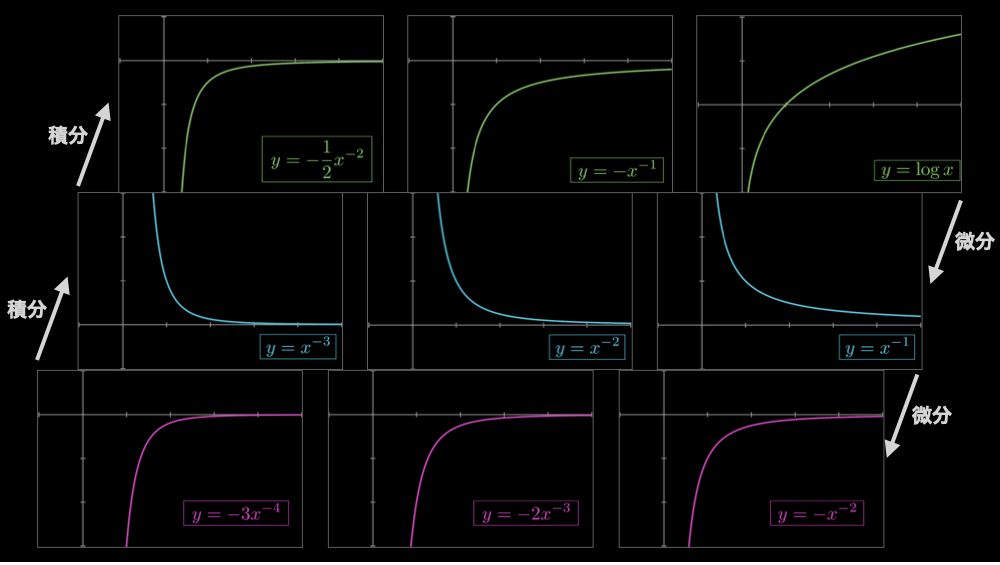
このようにベキ指数が−２以下の場合は、微分した結果と積分した結果はグラフを反転したものになります。
このベキ乗関数の微積分の視覚的（幾何学的）な性質は、試験問題で高得点を取る目的にはあまり役立ちませんが、微積分を現実世界の現象を理解するために活用する目的には大いに役立ちますので、ぜひ覚えておいてください。
3.2. ベキ乗関数の微積分の規則性の例外
さて上でも少し触れましたが、ベキ乗関数の微積分の連続性には例外があります。それが \(y=x^{-1}(=\frac{1}{x})\) の場合と \(y=x^0(=1)\) の場合です。次にこの点について見ていきましょう。
もう一度、以下の連続性の数式をご覧ください。
ベキ乗関数の微積分の規則性
\[
\begin{array}{ccc}
F(x): & -\dfrac{1}{2}x^{-2} & -x^{-1}& \bigcirc \ \log x & \ \ x \ \ & \ \ \dfrac{1}{2}x^2 \ \ & \ \ \dfrac{1}{3}x^3 \ \ \\
& \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow\\
f(x): & x^{-3} & x^{-2} & x^{-1} & x^0 & x^1 & x^2\\
& \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow\\
f^{\prime}(x): & -3x^{-4} & -2x^{-3} & -x^{-2} & \bigcirc \ 0 & 1 & 2x^1
\end{array}
\]
大きな◯を付けている部分だけ、連続性の例外になっています。
つまり、規則性からしたら、ベキ指数 \(n=-1\) のときは、積分をすると \(n=0\) になるはずです。しかし、実際には規則性に反して \(\log x\) というものが出てきます。
\[
\int x^{-1}dx=\log x
\]
同じく、規則性からしたら、ベキ指数 \(n=0\) のときは、微分をすると \(n=-1\) になるはずですが、実際には値が \(0\) になります。
\[
\dfrac{dx^0}{dx}=0
\]
詳しくはオフトピックになるので控えますが、これは「実数の世界から虚数の世界への入り口」というように理解しておくと良いでしょう。虚数について学ぶときは、ぜひ、この点を思い出してみてください。
4. ベキ乗関数の積分のまとめ
以上がベキ乗関数の積分公式と、その性質です。
冒頭でもお伝えした通り、ベキ乗関数は現実世界のあらゆる現象を表している関数であり、これの微分積分を深く理解することは、それらの現象を深く理解することにつながります。
そのため積分公式を覚えることはもちろんですが、それだけでなく、ベキ乗関数の積分の規則性も含めて、しっかりと理解するように心がけましょう。そこまで意識して学ぶようにすると、現実世界における問題解決能力が身に付きます。それは数学パズルを解けるだけの場合よりも遥かに有益です。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント