べき乗の微分・累乗の微分はどちらも同じ公式で簡単に求めることができます。その公式を知っておけば、べき乗の微分は、わざわざ微分の定義式から計算する必要なく、素早く簡単に求められるようになります。
それが以下の公式です。
べき乗の微分公式
\[(x^n)^{\prime}=nx^{n-1}\]
なお、べき乗・累乗はどちらも \(x^n\) の計算のことです。ただし、べき乗では \(n\) は自然数を含む全ての実数 (\(-1, \frac{1}{2}, \pi\) など) ですが、累乗は \(n\) が自然数(\(1,2,3\) など)に限定されます。
\[
\underbrace{
\overbrace{
x^1,
\hspace{5mm}
x^2,
\hspace{5mm}
x^3}^{累乗},
\hspace{5mm}
x^{-1},
\hspace{5mm}
x^{\frac{1}{2}},
\hspace{5mm}
x^\pi}_{べき乗}\]
そして、べき乗でも累乗でも、微分は全て上の公式で簡単に求めることができます。例えば以下のようになります。
\[
(x^2)^{\prime}=2x, \hspace{7mm}
(x^{-1})^{\prime}=-x^{-2}, \hspace{7mm}
(x^{\frac{1}{3}})^{\prime}=\frac{1}{3}x^{-\frac{2}{3}}
\]
それではなぜ、この公式でべき乗の微分を求めることができるのでしょうか。このページでは、この理由について、誰でも直観的に理解できるように、アニメーションと画像を豊富に使いながら解説していきます。
ぜひじっくりご覧頂ければと思います。
1. べき乗の微分公式の解説
まずは累乗の場合から見ていきましょう。累乗関数の微分は、指数部分がどれだけ大きくなっても必ず \(nx^{n-1}\) になります。
累乗の微分
\[\begin{eqnarray}
(x^1)^{\prime}&=&1\\
(x^2)^{\prime}&=&2x\\
(x^3)^{\prime}&=&3x^2\\
&\vdots&\\
(x^{100})^{\prime}&=&100x^{99}\\
\end{eqnarray}\]
なぜ、こうなるのでしょうか。
これは \(x^2\) と \(x^3\) の微分がどういうことかを、視覚的に把握することで、とても簡単に理解することができます。
1.1. \(x^2\) の微分の解説
まず \(f(x)=x^2\) から考えてみましょう。
この関数は言ってみれば \(x \times x\) という2つの値の掛け算です。微分学の世界では、このような2つの値の掛け算は、以下のアニメーションで示しているように、四角形の面積に置き換えてイメージするのが定番です。
このように \(x^2\) は辺の長さが \(x\) の正方形の面積として解釈することができます。当然、この正方形の面積は \(x\) の値によって変わります。
さて、『微分とは何か?誰でもわかりやすく理解できるようにイメージで解説』で解説した通り、微分とは、\(x\) の値が \(dx\) というほんの一瞬だけ変化したときの瞬間変化率です。
そして瞬間の変化率は、\(\frac{dy}{dx}\) で計算するため、対象となる関数が何であったとしても、微分を深くイメージできるようになるためのコツは、\(dx\) と、それによる関数の値の変化である \(dy=df(x)\) を視覚的に把握することにあります(\(d\) は \(\Delta\) と同じく変化量を意味する記号です。しかし \(d\) は「非常に小さな変化」を意味します)。
それでは \(x\) の値が \(dx\) だけ増加したら、この面積 \(df(x)\) はどう変化するでしょうか?
もちろん \(dx\) に応じて正方形の面積も \(df\) だけ増加します( \(df\) は \(d(f(x))\) を省略したものです)。以下のアニメーションで示している通りです。
ご覧の通り、この面積の増加分 \(df\) は2つの大きな長方形 \(x \times dx\) と、1つの小さな正方形 \(dx \times dx\) の合計 \(2x(dx)+(dx)^2\) で求められます。
増加面積 \(df\) の計算方法
\[df=2x(dx)+(dx)^2\]
さて、微分の定義上、\(dx\) は限りなく0に近い値です。そのため、増加面積において、0に近い値を2回掛けている \((dx)^2\) の部分は、もう0とみなして良いほどの値になっています。このことから実際には、 \(2x(dx)\) の部分が増加面積の99.99999999 \(\cdots\) %を占めていることがわかります。
このことは、上のアニメーションでは \(dx\) の値を大きく取っているのでピンと来ないかもしれませんが、以下のように、実際に \(dx\) を0に近づけるとわかりやすくなります。
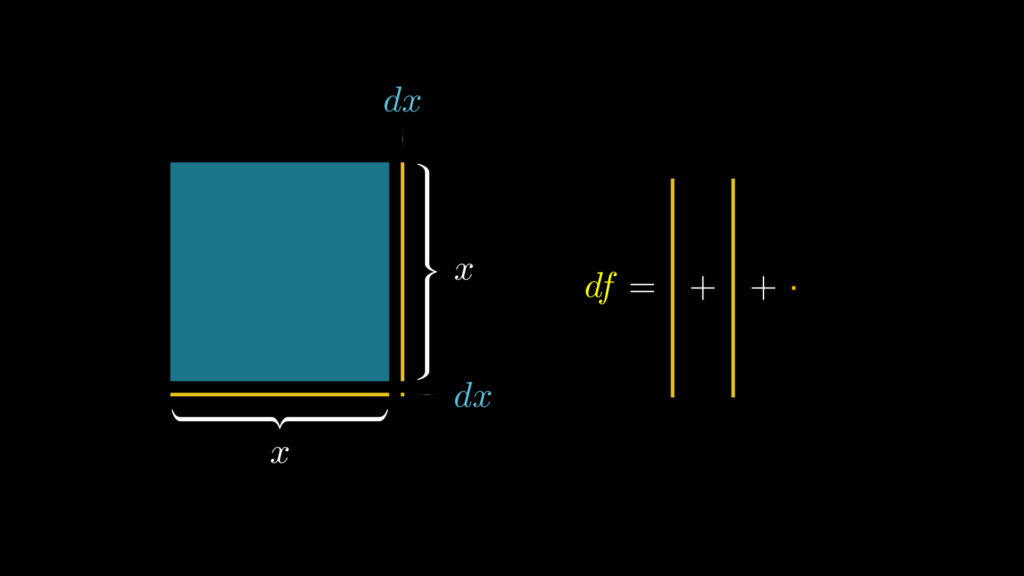
明らかに \(dx^2\) の面積は、\(x(dx)\) と比べると、計算に入れる必要がないほど小さくなっていることがわかります。
以上のことから、実際の増加面積は \(df=2x(dx)\) と考えて良いことになります。そして、微分はこの面積の瞬間的な変化率(増加率)なので、以下の通り、この増加面積を一瞬の間である \(dx\) で割ったものです。
面積の変化率
\[\dfrac{df}{dx}=\dfrac{2x(dx)}{dx}=2x\]
※見切れている場合は右にスクロールすることができます。
以上のことから \(x^2\) の微分(=面積の瞬間の変化率)は \(2x\) となることがわかりました。
1.2. \(x^3\) の微分の解説
次は同じように \(f(x)=x^3\) について考えてみましょう。この計算は \(x\times x \times x\) と同じです。このような3つの値の掛け算は、立方体の体積に置き換えて考えるのがコツです。
参考に以下のアニメーションをご覧ください。
さて、それでは \(x\) の値が \(dx\) だけ増加したら \(dy=df(x)\) である体積はどう変化するでしょうか。もちろん増加します。以下のアニメーションでご確認ください。
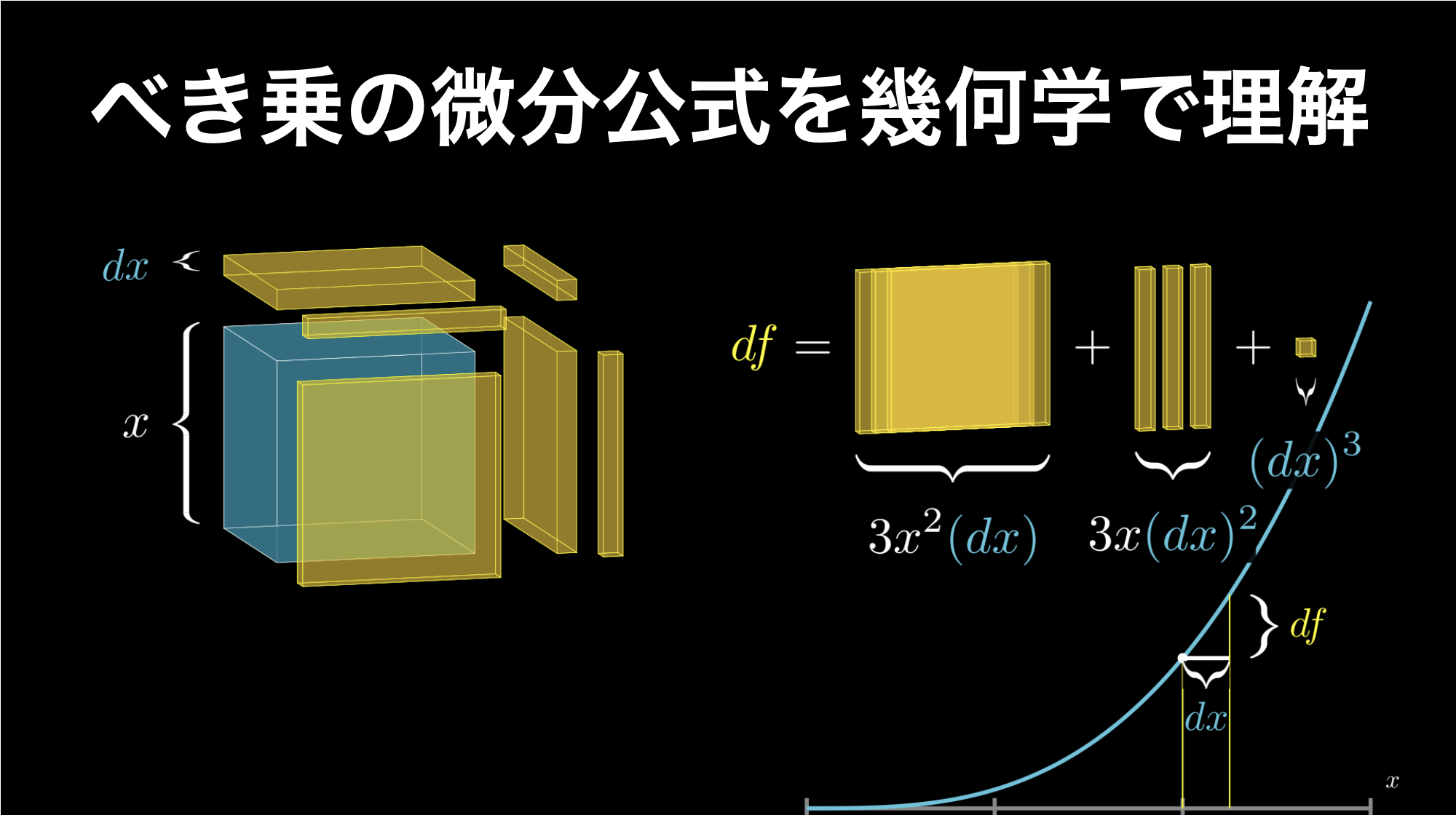
ご覧の通り、増えた体積 \(df\) は3つの大きな六面体 \(x \times x \times dx\) と、3つの細長い小さな六面体 \(x \times dx \times dx\)、そして1つの非常に小さな立方体 \(dx \times dx \times dx\) の合計である \(3x^2(dx)+3x(dx)^2+dx^3\) になります。
増加体積
\[df=3x^2(dx)+3x(dx)^2+dx^3\]
しかし、\(x^2\) の時と同じように、\(dx\) は限りなく0に近い値であるため、これを2回以上掛けている部分は、実質的には 0と同じであると考えて良いことになります。つまり、最も大きな3つの六面体が増加体積の99.99999999 \(\cdots\) %を占めているのです。
このことは以下の画像で示している通り、\(dx\) をもっと小さくすると、視覚的にもわかりやすくなります。
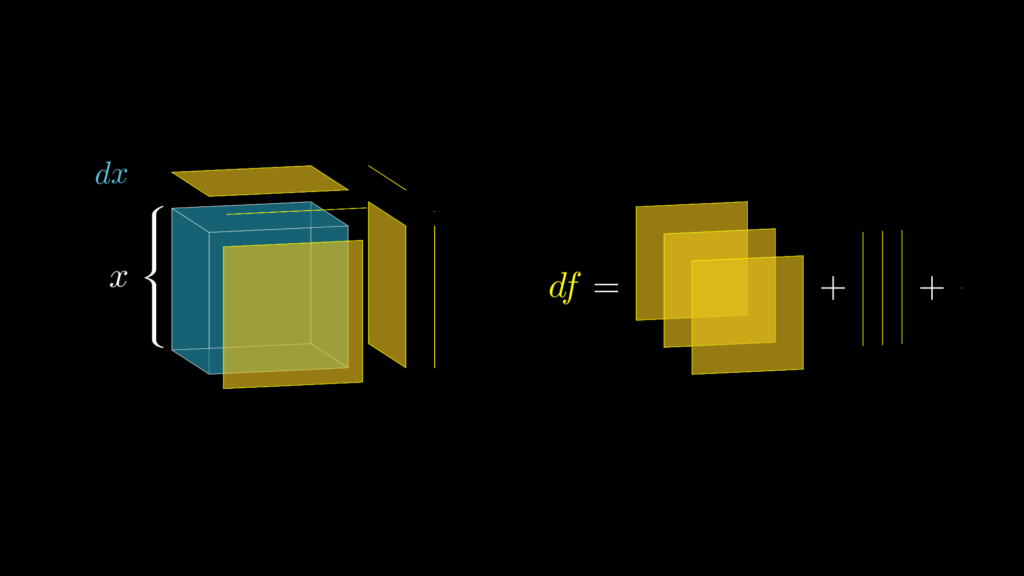
このことから増加体積は、実質的には \(df=3x^2(dx)\) になります。そして微分はこの体積の瞬間的な変化率(増加率)なので、\(dx\) で割って以下のように計算します。
体積の変化率
\[\dfrac{df}{dx}=\dfrac{3x^2(dx)}{dx}=3x^2\]
以上のことから \(x^3\) の微分(=体積の瞬間の変化率)は \(3x^2\) になることがわかります。
1.3. \(x^n\) の微分の証明
それでは \(x^4\) 以上の微分はどうなるでしょうか?こうなると4次元空間になってしまうので、人間の脳ではイメージすることは不可能です。そこで数式の出番になります。
なお、ここからは微分の定義式を使います。定義式については『微分とは何か?誰でもわかりやすく理解できるようにイメージで解説』で解説していますので、理解に自身がない場合はぜひご確認ください。
微分の定義式
\[
\frac{dy}{dx}=\lim_{dx \to 0} \frac{f(x+dx)-f(x)}{dx}
\]
ここまで見てきた \(x^2\) と \(x^3\) は、この定義式に当てはめると、以下のようになります。
\(f(x)=x^2\) の場合
\[\begin{eqnarray}
\dfrac{dy}{dx}
&=&
\dfrac{(x+dx)^2-x^2}{dx}\\
&=&
\dfrac{x^2+2x(dx)+(dx)^2-x^2}{dx}\\
&=&
\dfrac{2x(dx)+(dx)^2}{dx}\\
&=&
2x+dx\\
&=&
2x
\end{eqnarray}\]
※見切れている場合は右にスクロールすることができます。
\(f(x)=x^3\) の場合
\[\begin{eqnarray}
\dfrac{dy}{dx}
&=&
\dfrac{(x+dx)^3-x^3}{dx}\\
&=&
\dfrac{x^3+3x^2(dx)+3x(dx)^2+dx^3-x^2}{dx}\\
&=&
\dfrac{3x^2(dx)+3x(dx)^2+dx^3}{dx}\\
&=&
3x^2+3x(dx)+dx^2\\
&=&
3x^2
\end{eqnarray}\]
※見切れている場合は右にスクロールすることができます。
このように見てみると、定義式の \(f(x+dx)-f(x)\) の部分が面積や体積の増加分に該当することがわかります。
\[
\underbrace{\underbrace{f(x+dx)}_{全体面積(体積)}-\underbrace{f(x)}_{元の面積(体積)}}_{増加面積(体積)}\]
さて、ここまでで見てきた \(x^2\) の微分と \(x^3\) の微分には同じ法則がありました。その法則とは、\(x^2\) では \(dx\) による増加面積のほぼすべてが、もっとも大きな2つの長方形で成り立っており、\(x^3\) では \(dx\) による増加体積のほぼすべてが、もっとも大きな3つの六面体で成り立っているということです。
別の言い方をすれば、面積や体積の増加分の99.9999 \(\cdots\)%は、\(dx\) が一回だけ掛かっている部分によるものであり、\(dx\) が2回以上掛かっている部分は無視できるほど小さいということです。
そしてこの法則は、ここまで見てきたアニメーションやイメージから類推できるように、すべての \(x^n\) に対して当てはまります。なぜなら、\((x+dx)^n-x^n\) の部分を展開すると、以下に示している通りになるからです。
\[\begin{eqnarray}
(x+dx)^n-x^n
&=&
\overbrace{(x+dx)(x+dx)(x+dx)\cdots(x+dx)}^{n回}\\
&=&
x^n+nx^{n-1}dx+\overbrace{(\cdots \cdots \cdots)}^{dx^2 以上の掛け算}-x^n\\
&=&
nx^{n-1}dx+\overbrace{(\cdots \cdots \cdots)}^{\approx 0}
\end{eqnarray}\]
※見切れている場合は右にスクロールすることができます。
以上のことから、べき乗の微分の公式が成り立つことが証明されます。
\[\begin{eqnarray}
\dfrac{dy}{dx}
&=&
\dfrac{(x+dx)^n-x^n}{dx}\\
&=&
\dfrac{nx^{n-1}dx+\overbrace{(\cdots \cdots \cdots)}^{dx^2 以上の掛け算}}{dx}\\
&=&
nx^{n-1}dx
\end{eqnarray}\]
2. べき乗の微分公式の応用
ここまでは、\(x^n\) において \(n\) が自然数の場合を見てきました。それでは、\(n\) が負の値や分数の場合はどうなるでしょうか?
もちろん全く同じになります。例えば、\(x^{-1}\)の微分は次のようになります。
\[
(x^{-1})^{\prime}=-1x^{-2}
\hspace{3mm}
\Longleftrightarrow
\hspace{3mm}
(\dfrac{1}{x})^{\prime}=-\dfrac{1}{x^2}
\]
そして、\(x^{\frac{1}{2}}\)の微分は次のようになります。
\[
(x^{\frac{1}{2}})^{\prime}=\dfrac{1}{2}x^{-\frac{1}{2}}
\hspace{3mm}
\Longleftrightarrow
\hspace{3mm}
(\sqrt{x})^{\prime}=\dfrac{1}{2\sqrt{x}}
\]
このように、\(n\)が自然数以外の実数の場合でも、何も考えずに、べき乗の微分公式を当てはめることで簡単に解くことができます。しかし、これがどういうことなのかを幾何学的(視覚的)に理解しておくことには、とても大きな意味があります。
そういうわけで、これらについても理解を深めていきましょう。
2.1. \(x^{-n}\)の微分の解説
\(x^{-1}=\dfrac{1}{x}\) のような負の数のべき乗は、以下に示しているように、元の数 \(x\) に掛けると \(1\) になるような数を意味しています。
負の数のべき乗の意味
\[\begin{eqnarray}
x^{-1}\cdot x &=& 1\\
x^{-2}\cdot x^2 &=& 1\\
&\vdots&\\
x^{-n}\cdot x^n &=& 1
\end{eqnarray}\]
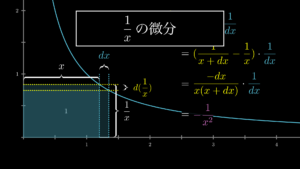
ここでは、例として \(x^{-1}\) の微分を考えてみましょう。このような負の値のべき乗関数は、以下のアニメーションで示しているように、面積が常に1の長方形に置き換えてイメージできます。
さて、ここまで繰り返し見てきたように、微分を考えるということは、\(x\) の値がわずかに \(dx\) だけ変化したときの変化率を見るということです。
そして関数、\(f(x)=x^{-1}\) では、\(x\) の値が \(dx\) 増加すると、以下のアニメーションで示している通り、長方形の長さが \(dx\) 増加し、高さが \(d(\frac{1}{x})\) 減少します。この高さの変化を、長さの変化で割ったものが微分です。
このように、\(x^n\) において \(n\) が負の値のべき乗関数は、全て、同じように面積が常に1の長方形をイメージすることで、とても理解しやすくなります。
ぜひ一度、\(x^{-2}\) や \(x^{-3}\) の場合にどうなるかも考えてみてください。そうしたことを考えていると、驚くほど応用力が鍛えられていきます。
なお、べき指数の部分が負の値のべき乗関数の微分については、『1/xの微分が誰でもすぐに簡単に理解できるようになる解説』でも解説しているので、ぜひ併せてご確認ください。
2.2. \(x^{\frac{1}{n}}\) の微分の解説
続いて分数のべき乗の微分を考えてみましょう。分数のべき乗の意味は以下に示している通りです。
分数のべき乗の意味
\[\begin{eqnarray}
x^{\frac{1}{2}} \cdot x^{\frac{1}{2}} &=&x \\
x^{\frac{1}{3}} \cdot x^{\frac{1}{3}} \cdot x^{\frac{1}{3}} &=& x\\
x^{\frac{1}{4}} \cdot x^{\frac{1}{4}} \cdot x^{\frac{1}{4}} \cdot x^{\frac{1}{4}} &=& x\\
& \vdots & \\
x^{\frac{1}{n}} \cdot x^{\frac{1}{n}} \cdot x^{\frac{1}{n}} \cdot x^{\frac{1}{n}} \cdots x^{\frac{1}{n}} &=& x
\end{eqnarray}\]
このように分数のべき乗は、複数回掛けると \(x\) になるような数を意味します。さて、それではこれの微分はどうなるでしょうか。\(x^{\frac{1}{2}}(=\sqrt{x})\) の微分を例に考えてみましょう。
まず、\(x^{\frac{1}{2}}\) は、以下のアニメーションで示しているように、面積が \(x\) の正方形の「辺」に置き換えてイメージすることができます。
それでは、この関数においては \(dx\) は何を意味するでしょうか。少し考えてみてください。\(x\) の値が面積を意味するということは…?そう関数 \(x^{\frac{1}{2}}\) では、\(dx\) は面積の増加分を意味するのです。以下のアニメーションで、このことをわかりやすく示しています。
さて、このように見てみると \(dx\) の値は、増加した面積 \(2(d\sqrt{x})(\sqrt{x})+(d(\sqrt{x}))^2\) と等しくなることがわかります。そして、ここまで見てきた通り、\((d(\sqrt{x}))^2\) はあまりにも小さい数であるため無視できますので、実質的には \(dx=2(d\sqrt{x})(\sqrt{x})\) になります。
あとは以下の通り \(\dfrac{dy}{dx}\) を計算すると公式通りの解が得られることがわかります。
\[\begin{eqnarray}
\dfrac{dy}{dx}&=&\dfrac{d(\sqrt{x})}{2(d(\sqrt{x}))(\sqrt{x})}\\
&=&
\dfrac{1}{2(\sqrt{x})}
\end{eqnarray}\]
\(x^{\frac{1}{3}}\) の場合も、まったく同じように考えることができます。辺の長さが \(\sqrt[3]{x}\) の立方体の体積が \(x\) になります。これについては、ご自身で書き出しながら考えてみて頂ければと思います。このように幾何学的に理解しておくと、公式を暗記する必要がなくなっていきますので、ぜひチャレンジしてみてください。
なお、べき指数の部分が分数のべき乗関数の微分については、『ルート(√x)の微分を誰でも簡単に深く理解できるように解説』でも解説しているので、ぜひ併せてご確認ください。
3. べき乗の微分公式のまとめ
以上がべき乗の微分公式と、その証明です。
公式の証明を、ここまで解説してきたように幾何学的なイメージで理解しておくと、より高度な数学を扱うときに非常に大きな助けとなります。また、統計学であれ、コンピューターサイエンスであれ、数学が重要な分野の知識を一歩先へと深める目的にもとても適しています。
ぜひ参考にして頂ければと思います。




コメント