ここではルート（√x）の微分について、誰でも深く理解できるように解説していきます。なお、先に『1/xの微分が誰でもすぐに簡単に理解できるようになる解説』をご覧頂いておくと、より理解しやすくなりますので、ぜひ合わせてご覧ください。
それでは早速始めましょう。
1. ルートの微分の求め方
結論から言うと、ルートの微分は、べき乗の微分公式を使うと簡単に求めることができます。なぜなら、以下で示している通り、ルートとはべき指数が分数のべき乗だからです。
ルートはべき指数が分数のべき乗
\[\begin{eqnarray}
\sqrt{x}=x^{\frac{1}{2}}&\rightarrow&(x^{\frac{1}{2}} \cdot x^{\frac{1}{2}} =x)\\
\sqrt[3]{x}=x^{\frac{1}{3}} &\rightarrow& (x^{\frac{1}{3}} \cdot x^{\frac{1}{3}} \cdot x^{\frac{1}{3}} = x)\\
& \vdots &\\
\sqrt[n]{x}=x^{\frac{1}{n}} &\rightarrow& (x^{\frac{1}{n}} \cdot x^{\frac{1}{n}} \cdot x^{\frac{1}{n}} \cdots x^{\frac{1}{n}} = x)\\
\end{eqnarray}\]
そのため √x の微分は以下のように、べき乗の微分公式から簡単に求められます。
ルートの微分をべき乗の微分公式で求める
\[\begin{eqnarray}
(\sqrt{x})^{\prime}&=&(x^{\frac{1}{2}})^{\prime}\\
&=&
\frac{1}{2}x^{-\frac{1}{2}}\\
&=&
\frac{1}{2} \cdot \frac{1}{\sqrt{x}}\\
&=&
\frac{1}{2\sqrt{x}}
\end{eqnarray}\]
このように、ルートの微分を解くポイントは、ルートを、指数部分が分数であるべき乗関数として解釈するところにあります。
単純に微分問題を解くだけなら、ここまでを押さえておけば十分です。
しかし、微分の応用分野に進むなら、より深く微分を理解しておいた方が断然有利です。そこで、次からルートの微分についてもっと深く考えていきましょう。
2. ルートの微分を視覚的に解説
ここからルートの微分を深く理解できるように、視覚的（幾何学的）に解説していきます。
なお、前提として、累乗（べき指数が自然数のべき乗）は、以下の画像のように、四角形の面積や立方体の体積としてイメージすると深く理解できるという点を思い出しておいて下さい（まだ『べき乗（累乗）の微分公式-誰でも必ず深く理解できるように解説-』をご覧になっていない場合は、ぜひ先にご覧ください）。
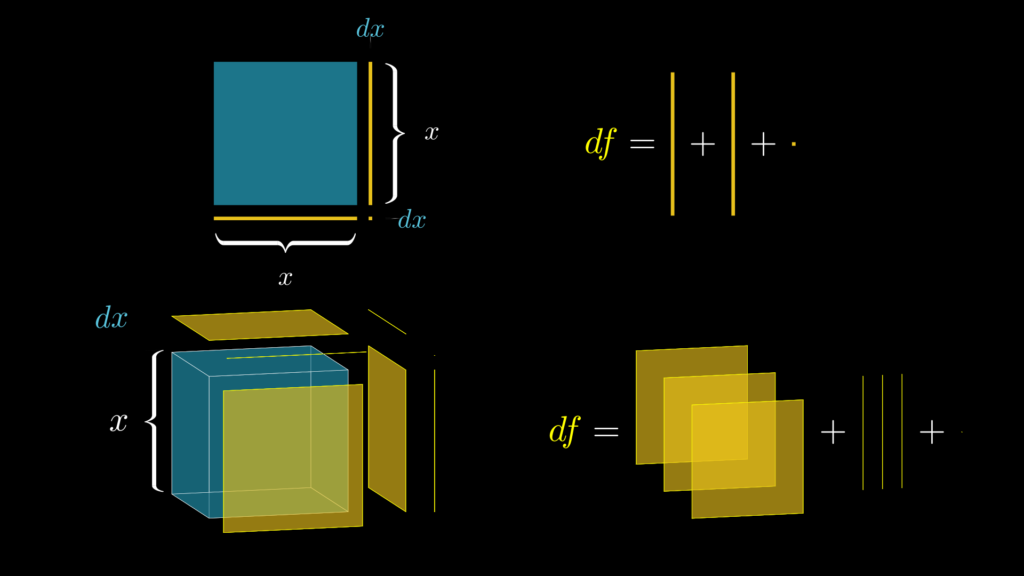
それでは、べき指数が分数であるべき乗関数 \(x^{\frac{1}{2}}\) は、幾何学的にはどのようにイメージできるでしょうか？
これは以下のアニメーションで示している通り、両辺の長さが \(\sqrt{x}\) で面積が常に \(x\) の正方形として考えることができます。
さて、『微分とは何か？誰でもわかりやすく理解できるようにイメージで解説』で解説している通り、微分とは \(x\) の値がわずかに \(dx\) だけ変化したときの瞬間の変化率です。
この \(dx\) と、それによる変化を視覚的に把握すれば、微分はとてもよくわかるようになります。それでは関数 \(x^{\frac{1}{2}}\) においては \(dx\) は何を意味するでしょうか。
少し考えてみてください。
\(x\) の値が面積を意味するということは、関数 \(x^{\frac{1}{2}}\) では、\(dx\) は面積の増加分を意味することになります。以下のアニメーションで、このことをわかりやすく示しています。
さて、このように見てみると \(dx\) の値は、増加した面積 \(2(d\sqrt{x})(\sqrt{x})+(d(\sqrt{x}))^2\) と等しくなることがわかります。そして、\((d(\sqrt{x}))^2\) は無視できるほど小さい数であるため、実質的には \(dx=2(d\sqrt{x})(\sqrt{x})\) になります。あとは微分の定義式の通り、\(\frac{dy}{dx}\) から簡単に計算することができます。
実際の数式は以下の通りです。
ルートの微分の証明（微分の定義式より）
\[\begin{eqnarray}
\frac{dy}{dx}
&=&
\frac{d(\sqrt{x})}{2(d\sqrt{x})(\sqrt{x})+(d(\sqrt{x}))^2}\\
&=&
\frac{d(\sqrt{x})}{2(d\sqrt{x})(\sqrt{x})}\\
&=&
\dfrac{1}{2\sqrt{x}}
\end{eqnarray}\]
なお、\(x^{\frac{1}{3}}\) の場合は、各辺が \(\sqrt[3]{x}\) で体積が \(x\) の立方体をイメージすると、より深く理解できるようになります。ぜひ一度ご自身でチャレンジしてみてください。
3. ルートの微分まとめ
以上がルートの微分です。
まとめると、ルートを、指数部分が分数のべき乗として解釈すると、べき乗の微分公式を使って簡単に解くことができます。数学の問題を解くだけであれば、この理解だけで十分です。もし微分をより深く理解できるようになりたいという場合は、ぜひ幾何学的なイメージもしっかりと頭に入れておくようにしましょう。
ぜひ参考にして頂ければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
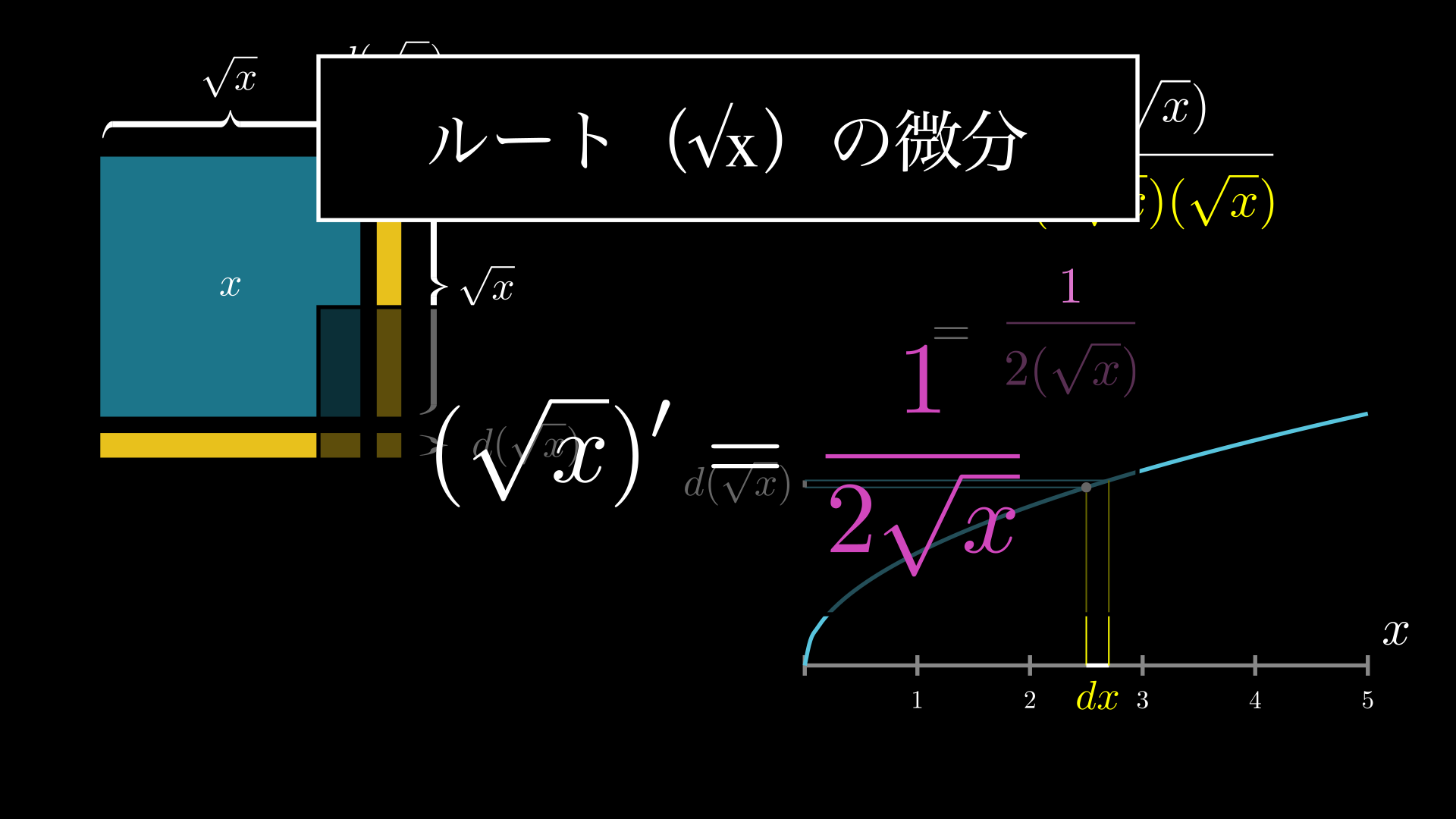
コメント