ここでは重要な微分公式の一覧と、それぞれの公式がよく理解できるようになる解説ページへのリンクを用意しています。
公式を暗記しようとするのではなく、そのようになる理由を説明している解説ページも、ぜひ確認するようにしてください。そうすれば、暗記の必要なく自然と公式を覚えられるようになりますし、数学的な応用力が身に付きます。
それでは早速見ていきましょう。
1. 微分の定義
まずはすべての基本となる微分の定義式を確認しておきましょう。
微分の定義式
\[
f^{\prime}(x)
=
\dfrac{f(x+dx)-f(x)}{dx}
\]
詳しくは『微分とは何か？誰でもわかりやすく理解できるようにイメージで解説』で解説しています。
2. 導関数の公式
まずは導関数の公式を列挙します。
2.1. べき乗の微分
べき乗関数の微分公式
\[
(x^n)^{\prime}=nx^{n-1}
\]
詳しくは『べき乗（累乗）の微分公式を誰でも必ず深く理解できるように解説』で解説しています。
なお \(\frac{1}{x}\) と \(\sqrt{x}\) の微分も、この公式で解くことができます。
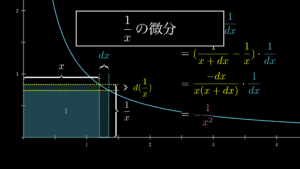
1/x の微分
\[\begin{eqnarray}
\frac{1}{x}^{\prime}= (x^{-1})^{\prime}=-\frac{1}{x^2}
\end{eqnarray}\]
詳しくは『1/xの微分を誰でも簡単に理解できるように解説』をご覧ください。
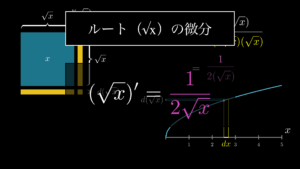
√x の微分
\[\begin{eqnarray}
\sqrt{x}^{\prime}= (x^{\frac{1}{2}})^{\prime}=\frac{1}{2\sqrt{x}}
\end{eqnarray}\]
詳しくは『ルート（√x）の微分を誰でも簡単に深く理解できるように解説』をご覧ください。
2.2. 三角関数の微分
三角関数の微分はそれぞれ以下の通りです。詳しい解説は『三角関数の微分が誰でも驚くほどよく分かるようになる解説』をご覧ください。また、以下の３つのページでも個別に解説しています。
sinの微分公式
\[
\sin(x)^{\prime}=\cos(x)
\]
cosの微分公式
\[
\cos(x)^{\prime}=-\sin(x)
\]
tanの微分公式
\[
\tan(x)^{\prime}=\frac{1}{\cos^2(x)}
\]
2.3. 指数関数の微分
指数関数の微分は以下の通りです。
指数関数の微分公式
\[\begin{eqnarray}
(e^x)^{\prime}&=&e^x\\
(a^x)^{\prime}&=&a^x \log_ea
\end{eqnarray}\]
詳しくは『指数関数の微分を誰でも理解できるように解説』で解説しています。
2.4. 対数関数（log）の微分
対数関数 (log) の微分は以下の通りです。
対数関数の微分公式
\[\begin{eqnarray}
(\log_ex)^{\prime}&=&\dfrac{1}{x}\\
(\log_ax)^{\prime}&=&\dfrac{1}{x \log_e a}
\end{eqnarray}\]
詳しくは『log（対数関数）の微分を誰でも理解できるように丁寧に解説』で解説しています。
2.5. 逆関数の微分
逆関数の微分は以下の通りです。
逆関数の微分公式
\[\begin{eqnarray}
g^{\prime}(y)=\dfrac{1}{f^{\prime}(x)}
\end{eqnarray}\]
※ \(y=f(x), \hspace{5mm} x=g(y)\)
詳しくは『逆関数の微分を誰でも理解できるように視覚的に解説』をご覧ください。
3. 演算公式
続いて演算公式を列挙します。
3.1. 和の微分法則
関数の和の微分は以下の通りです。
和の微分法則
\[
(f(x)\pm g(x))^{\prime}=f^{\prime}(x) \pm g^{\prime}(x)
\]
詳しくは『和の微分公式（微分の足し算・引き算）が直感的に理解できる解説』で解説しています。
3.2. 定数倍の微分法則
関数の定数倍の微分は次の通りです。
定数倍の微分法則
\[
(cf(x))^{\prime}=cf^{\prime}(x)
\]
詳しくは『定数倍の微分公式が誰でも直感的にわかるようになる解説』で解説しています。
3.3. 積の微分法則
関数の積の微分は以下の通りです。
積の微分法則
\[
(f(x)g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)
\]
詳しくは『積の微分公式を誰でも直感的に理解できるように解説』で解説しています。
3.4. 合成関数の微分法則
合成関数の微分は以下の通りです。
合成関数の微分法則
\[
(f(g(x)))^{\prime}=f^{\prime}(g(x))g^{\prime}(x)
\]
詳しくは『合成関数の微分を誰でも直観的かつ深く理解できるように解説』で解説しています。
3.5. 商（分数）の微分法則
関数の分数の微分は以下の通りです。
分数の微分法則
\[
\left\{
\frac{1}{f(x)}
\right\}
{}^{\prime}
=
-\frac{f^{\prime}(x)}{\{f(x)\}^2}
\]
商の微分法則
\[
\left\{
\dfrac{g(x)}{f(x)}
\right\}
{}^{\prime}
=
\dfrac{g^{\prime}(x)f(x)-f^{\prime}(x)g(x)}{\{f(x)\}^2}
\]
なお、これらは、べき乗関数の微分公式・積の微分公式・合成関数の微分公式をしっかりと理解していれば、覚えておく必要はありません。この点も含めて『分数関数の微分のやり方（商の微分公式）を誰でもわかるように解説』で解説しています。
4. 応用
ここでは大学レベル以上で学ぶことになる公式を列挙します。
4.1. 逆三角関数の微分
逆三角関数の微分は次の通りです。これらは『逆三角関数の微分を誰でも理解できるように解説』で詳しく解説しています。
また、以下のページでは、それぞれを個別に解説しています。
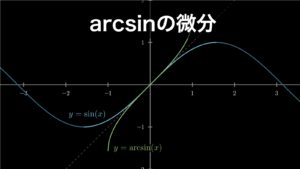
- 『arcsin（アークサイン）の微分を誰でもわかるように解説』
- 『arctan（アークタンジェント）の微分を誰でも理解できるように解説』
- 『arccos（アークコサイン）の微分を誰でも理解できるように解説』
arcsinの微分公式
\[
\arcsin(x)^{\prime}=\frac{1}{\sqrt{1-x^2}}
\]
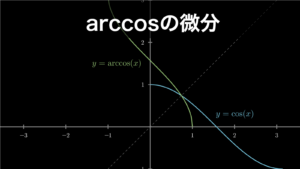
arccosの微分公式
\[
\arccos(x)^{\prime}=-\frac{1}{\sqrt{1-x^2}}
\]
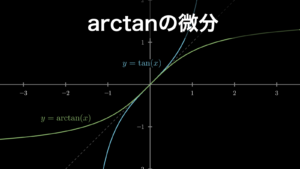
arctanの微分公式
\[
\arctan(x)^{\prime}=\frac{1}{1+x^2}
\]
4.2. 双曲線関数の微分
双曲線関数の微分は以下の通りです。
sinhの微分公式
\[
\sinh(x)^{\prime}=\cosh(x)
\]
coshの微分公式
\[
\cosh(x)^{\prime}=\sinh(x)
\]
tanhの微分公式
\[\begin{eqnarray}
\tanh(x)^{\prime}
&=&
1-tanh^2(x)\\
&=&
\frac{1}{\cosh^2(x)}
\end{eqnarray}\]
5. 微分公式のまとめ
以上が微分公式です。
冒頭でもお伝えしましたが、これらは暗記しようとするのではなく、理解しようとすることを心がけてください。そうすれば、微分問題などは、とても簡単に解けるようになります。そのためにも、ぜひ解説ページまで目を通していただければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント