合成関数の微分を誰でも直観的かつ深く理解できるように解説

2021 4/09

2021年4月9日 2021年4月9日

結論から言うと、合成関数の微分は (g(h(x)))’ = g'(h(x))h'(x) で求めることができます。これは「連鎖律」と呼ばれ、微分学の中でも非常に重要なものです。

そこで、このページでは、実際の計算例も含めて、この合成関数の微分について誰でも深い理解を得られるように、画像やアニメーションを豊富に使いながら解説していきます。

特に以下のようなことを望まれている方は、必ずご満足いただけることでしょう。

合成関数とは何かを改めておさらいしたい
合成関数の公式を正確に覚えたい
合成関数の証明を深く理解して応用力を身につけたい

それでは早速始めましょう。

1. 合成関数とは

合成関数とは、以下のように、ある関数の中に別の関数が組み込まれているもののことです。

合成関数

\[
f(x)=g(h(x))
\]

例えば g(x)=sin(x)、h(x)=x² とすると g(h(x))=sin(x²) になります。これはxの値を、まず関数 x² に入力して、その出力値であるx² を今度は sin 関数に入力するということを意味します。

x=0.5 としたら次のようになります。

合成関数のイメージ：sin(x^2)においてx=0.5 のとき

\[
0.5
\underbrace{\Longrightarrow}_{入力}
\overbrace{\boxed{h(0.5)}}^{h(x)=x^2}
\underbrace{\Longrightarrow}_{出力}
0.25
\underbrace{\Longrightarrow}_{入力}
\overbrace{\boxed{g(0.25)}}^{g(h)=sin(h)}
\underbrace{\Longrightarrow}_{出力}
0.247…
\]

このように任意の値xを、まずは内側の関数に入力し、そこから出てきた出力値を、今度は外側の関数に入力するというものが合成関数です。

参考までに、この合成関数をグラフにして、視覚的に確認できるようにしたものが下図です。

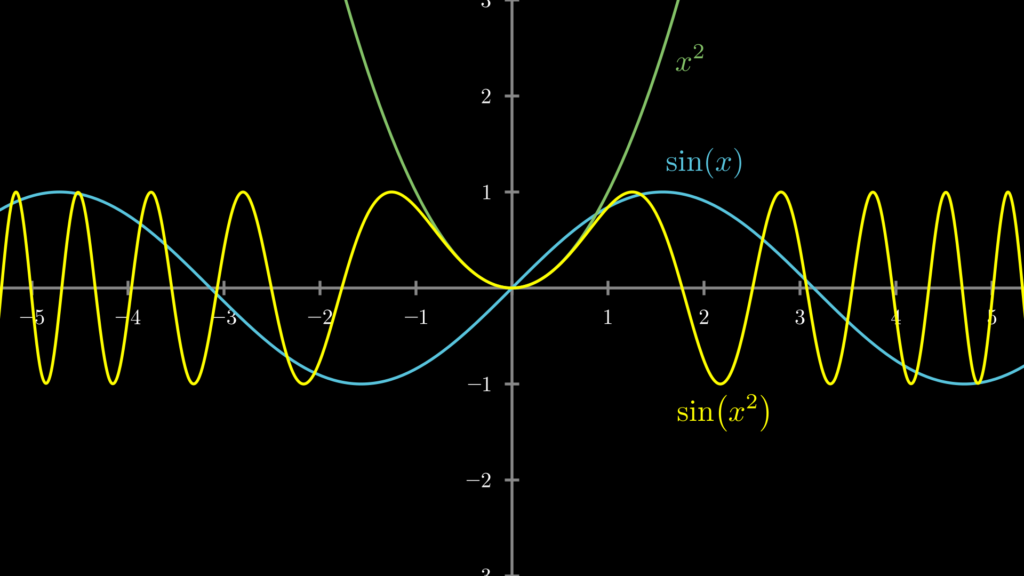
ご覧のように基本的に合成関数は複雑な曲線を描くことが多く、式を見ただけでパッとイメージできるようになるのは困難です。

それでは、この合成関数の微分はどのように求められるのでしょうか。

2.合成関数の微分公式

冒頭でもお伝えしましたが、合成関数の微分は次の公式の通りになります。

合成関数の微分公式（連鎖律）

\[
(g(h(x)))^{\prime}=g^{\prime}(h)\cdot h^{\prime}(x)
\]

この公式は「連鎖律 “Chain Rule”」と呼ばれており、以下のように３つのステップで成り立っています。

①まず外側の関数の微分を（内側の関数はそのままにして）求め、
②次に内側の関数の微分を求め、
③最後にそれらを掛け合わせる。

例として g(h(x))=sin(x²) を微分してみると以下のようになります。

\[\begin{eqnarray}
(\sin(x^2))^{\prime} &=& \overbrace{\sin^{\prime}(x^2)}^{外関数の微分} \cdot \overbrace{(x^2)^{\prime}}^{内関数の微分} \\
&=&\cos(x^2) \cdot 2x
\end{eqnarray}\]

この合成関数とその導関数をグラフに描くと下図のようになります。

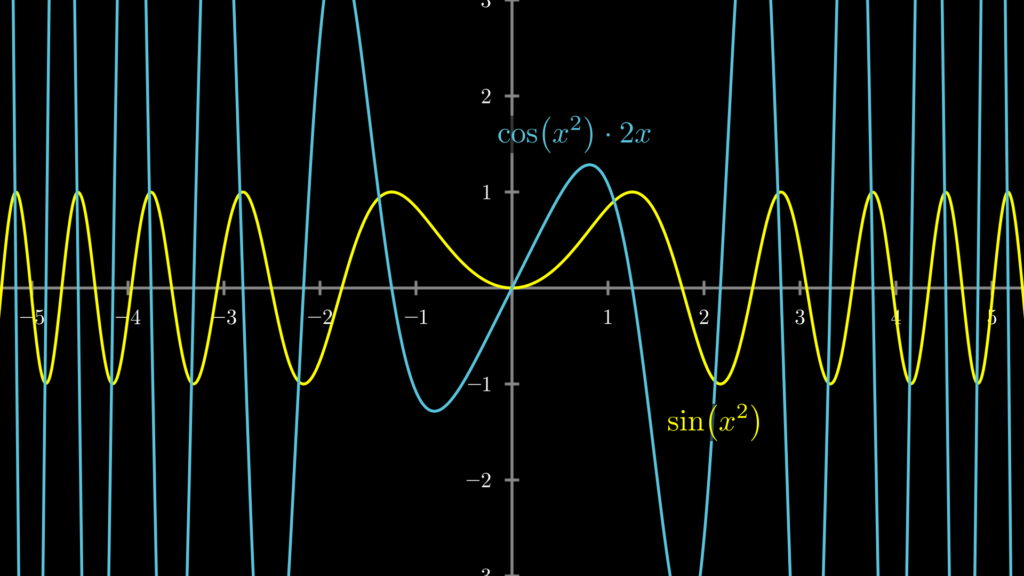
ちなみに、べき乗関数の微分と、sin関数の微分については、以下の記事で解説していますので、復習したい方はぜひご確認ください。

3.合成関数の微分の証明

さて合成関数の微分は、常に公式の通りになりますが、それはなぜなのでしょうか？この点について考えることで、単に公式を盲目的に使っている場合と比べて、微分をはるかに深く理解できるようになっていきます。

そこで、この点について深く考えていきましょう。

3.1. 合成関数は数直線でイメージする

合成関数の微分を理解するにはコツがあります。それは３本の数直線をイメージするということです。

上で見てきた通り、合成関数の曲線をグラフでイメージすることは非常に困難です。そのため数直線で代用するのですね。このことを早速、以下のアニメーションでご確認ください。

合成関数の微分を理解するコツは数直線でイメージすること

ご覧の通り、一番上の数直線は合成関数 g(h(x)) への入力値 x の値を表しています。そして真ん中の数直線は内側の関数 h(x) の出力値を表しています。最後に一番下の数直線は外側の関数 g(h) の出力値を表しています。

なお、関数 h(x) の出力値を h としています〈つまり g(h) と g(h(x)) は同じです〉。

3.2. 数直線上でxの変化による影響を把握する

さて、『微分とは何か？わかりやすくイメージで解説』で解説した通り、合成関数の微分とは、xの値が0に限りなく近い値であるdxだけ変化したときの、g(h) の値の変化率・・・です。

このときの合成関数の値の変化・・を d(g(h)) とすると、その変化率・・・は以下の計算式で求められるます。

合成関数の微分の計算式

\[
\frac{dy}{dx}
=
\frac{d(g(h))}{dx}
\]

以上のことから、合成関数の微分を深く理解するには、これらの変化 dxとd(g(h))がどのようなものかを、数直線上で紐解いていけば良いのですね。

それでは、実際に確認してみましょう。以下のアニメーションをご覧ください。

dx・d(h(x))・d(g(h))

このように、それぞれの数直線に書き込まれた色付きの直線が、xがdx変化したことによる h(x)の値の変化 d(h(x)) と、それによる g(h) の値の変化 d(g(h)) です。

このように、xの値が変化することで、まず内側の関数 h(x) の出力値が変化し、内側の関数の出力値が変化することで、外側の関数 g(h) の出力値が変化します。

そのため合成関数の微分は、以下のように、外側の関数の内側の関数に対する変化率を求め、次に、内側の関数のdxに対する変化率を掛け合わせるというものになるのです。

合成関数の微分の計算式②

\[\begin{eqnarray}
\frac{d(g(h))}{dx}=
\overbrace{\frac{d(g(h))}{d(h(x))}}^{外側の関数の変化率}
\cdot
\overbrace{\frac{d(h(x))}{dx}}^{内側の関数の変化率}
\end{eqnarray}\]

3.3. 微分の定義式を変換する

さて、微分の定義式を変換することで、 d(h(x)) は次のように書き換えられることがわかります。

\[
h^{\prime}(x)=\frac{d(h(x))}{dx}
\hspace{3mm}
\Longleftrightarrow
\hspace{3mm}
d(h(x))=h^{\prime}(x)dx
\]

これを使って今度は、d(g(h))を次のように書き換えることができます。

\[
g^{\prime}(h)=\frac{d(g(h))}{d(h(x))}=\frac{d(g(h))}{h^{\prime}(x)dx}
\hspace{3mm}
\Longleftrightarrow
\hspace{3mm}
d(g(h))=g^{\prime}(h) \cdot h^{\prime}(x)dx
\]

合成関数の微分は、これをdx で割ったものなので、これで合成関数の微分公式が求められます。以上を一つの式で表したものが、以下の式です。

合成関数の微分の証明

\[\begin{eqnarray}
g(h(x))^{\prime}
&=&
\frac{d(g(h))}{d(h(x))}
\cdot
\dfrac{d(h(x))}{dx}\\
&=&
\frac{g^{\prime}(h) \cdot h^{\prime}(x)dx}{h^{\prime}(x)dx}
\cdot
\frac{h^{\prime}(x)dx}{dx}\\
&=&
g^{\prime}(h) \cdot h^{\prime}(x)
\end{eqnarray}\]