三角関数の微分は、物理学や経済学・統計学・コンピューター・サイエンスなどの応用数学でも必ず使われており、微分の中でも使用頻度がもっとも高いものです。
具体的には、例えば、データの合成や解析に欠かすことができませんし、有名なフーリエ変換もsinとcosの組み合わせで可能となっている理論です。また、ベクトルの視覚化にも必要です。このように三角関数の応用例を全て書き出そうとしたら、それだけで日が暮れてしまうほどです。
とにかく、三角関数の微分は、絶対にマスターしておくべきトピックであるということです。
そこで、このページでは三角関数の微分について、誰でも深い理解を得られるように画像やアニメーションを豊富に使いながら丁寧に解説していきます。
ぜひじっくりとご覧になって、役立てていただければ嬉しく思います。
1. 三角関数とは
まずは三角関数について軽く復習しておきましょう。三角関数には、以下の３つがあります。
- sin（正弦）：単位円上の直角三角形の対辺の長さ（または対辺／斜辺）
- cos（余弦）：単位円上の直角三角形の隣辺（底辺）の長さ（または隣辺／斜辺）
- tan（正接）：単位円上の直角三角形の斜辺の傾き（=sin/cos）
厳密には、三角関数はこのほかにも、sec, csc, cot がありますが、まずはこの３つを理解することが大切です。基本の３つさえしっかりと理解すれば、その応用で他のものも簡単に理解できるようになります。
これらを深く理解するためのコツは、以下のアニメーションで示しているように、単位円上のなす角がθの直角三角形を使って、視覚的に把握しておくことにあります。
このように、三角関数を視覚的にイメージできるようになっておくことが、三角関数の微分の理解に大きく役立ちます。
2. 三角関数の微分
さて、それぞれの三角関数の微分公式（導関数）は、次の通りです。
三角関数の微分公式
\[\begin{eqnarray}
\sin^{\prime}(\theta) &=& \cos(\theta)\\
\cos^{\prime}(\theta) &=& -\sin(\theta)\\
\tan^{\prime}(\theta) &=& \frac{1}{\\cos^2(\theta)}
\end{eqnarray}\]
受験勉強では、この公式をそのまま丸暗記しておけば良いです。しかし、微分を将来の仕事や探究に活かそうとするなら、もっと深く理解しようとすることが大切です。
そこで、ここからは、それぞれの微分を、誰でもわかるように幾何学的（視覚的）に解説していきます。なお、数学の概念を幾何学的に理解しておくと、数式だけで理解する場合と比べて、はるかに応用力や発想力が身に付くようになります。実際、偉大な数学的発見の多くは、このような幾何学的発想から生まれていると言われています。
それでは、sin, cos, tanの微分をそれぞれ深く見ていきましょう。なお、これらは以下のページでも解説しています。正弦波・余弦波やラジアンの解説など、三角関数の微分の理解に重要で、かつ、当ページにない内容も追加していますので、ぜひ併せてご覧ください。
2.1. sinの微分
あらためて、sinの微分公式は次の通りです。
sinの微分公式
\[
\sin^{\prime}(\theta) = \cos(\theta)
\]
それでは、なぜこうなるのでしょうか？
微分（\(\frac{dy}{dx}\)）を理解するための鉄則は、dyとdxが何を意味するのかを視覚的にイメージできるようになることです。この視覚的なイメージの重要性については『微分とは何か？わかりやすくイメージで解説』をご覧頂ければ体感して頂けることでしょう。確認のためにも、ぜひご覧ください。
さて、三角関数の微分を理解するには、このような視覚的なイメージを、単位円上の直角三角形を用いて行うことがコツです。より具体的には、sin(θ)の微分は次のように計算します。
sinの微分の計算方法
\[
\sin^{\prime}(\theta)
=
\dfrac{\sin(\theta+d\theta)-\sin(\theta)}{d\theta}
=
\dfrac{d(\sin(\theta))}{d\theta}
\]
※見切れている場合は右にスクロールすることができます。
そのため、dθと d(sin(θ)) が何を意味するのかを単位円上の直角三角形で確認すれば良いのですね。これは以下のアニメーションをご覧頂ければ、とても理解しやすいでしょう。
このようにdθは孤の長さの変化で、d(sin(θ))はそれによる対辺の長さの変化です。そして、これらが形成している小さな直角三角形は、元の大きな直角三角形と相似形になっています。
このことから、sin'(θ) は隣辺／斜辺と同じ計算になっていることがわかります。そして、この計算はまさにcosの定義そのものです。以上のことから、sinの微分は必ずcosになるのですね。
cosの微分もtanの微分も、全く同じように単位円上で確認することで、簡単に理解することができます。続いて、簡潔に見ていきましょう。
2.2. cosの微分
cosの微分公式は次の通りです。
cosの微分公式
\[
\cos^{\prime}(\theta) = -\sin(\theta)
\]
cosの微分は具体的には以下の計算式で求められます。
cosの微分の計算方法
\[
\cos^{\prime}(\theta)
=
\dfrac{\cos(\theta+d\theta)-\cos(\theta)}{d\theta}
=
\dfrac{d(\cos(\theta))}{d\theta}
\]
※見切れている場合は右にスクロールすることができます。
さて、それでは dθとd(cos(θ)) は単位円上では何を意味するでしょうか。以下のアニメーションでご確認ください。
ご覧のようにsinの時と同じく、dθは孤の長さの変化で、d(cos(θ))はそれによる隣辺（底辺）の長さの変化です。そしてもちろん、これらが形成している小さな直角三角形は、元の大きな直角三角形と相似形になっています。
なお、dθが増加するとd(cos(θ))は減少し、dθが減少するとd(cos(θ))は増加するという負の関係になっています。そのため、両者は符号が必ず反対になる点にご注意ください。
以上のことからcos'(θ)は、−対辺／斜辺と同じ計算であることがわかります。そして、対辺／斜辺はまさにsinの定義と同じです。以上のことから、cosの微分は必ず-sinになることがわかります。
このようにsinの微分とcosの微分は全く同じように証明することができます。
それではtanの微分はどうでしょうか。単位円上でイメージすることは同じですが、sinとcosとは少し異なります。次にこれについて見ていきましょう。
2.3. tanの微分
tanの微分公式は次の通りです。
tanの微分公式
\[
\tan^{\prime}(\theta) = \dfrac{1}{\cos^2(\theta)}
\]
tanの微分は具体的には以下の計算式で求められます。
tanの微分の計算方法
\[
\cos^{\prime}(\theta)
=
\dfrac{\tan(\theta+d\theta)-\tan(\theta)}{d\theta}
=
\dfrac{d(\tan(\theta))}{d\theta}
\]
※見切れている場合は右にスクロールすることができます。
さて、それでは dθとd(tan(θ)) は単位円上では何を意味するでしょうか。以下のアニメーションでご確認ください。
ご覧のようにdθは孤の長さの変化で、d((tan(θ))はそれによる斜辺の傾きの変化です。そして、これらが形成している小さな直角三角形は、底辺を 1 、斜辺を 1/cos(θ)とする大きな三角形と相似形になっています。
このことから、小さな三角形の底辺である dθ/cos(θ) と斜辺である d(tan(θ)) の比率は、大きな三角形の底辺である 1 と斜辺である 1/cos(θ) と等しいものであることがわかります。
それによって、d(tan(θ))は次のように変換することが可能です。
\[
d(\tan(\theta))
=
\dfrac{d\theta}{\cos(\theta)} \cdot \dfrac{1}{\cos(\theta)}
=
\dfrac{d\theta}{\cos^2(\theta)}
\]
微分はこれをdθで割ったものなので、分子のdθが打ち消されて、最終的にtan(θ)の公式が導き出されます。
\[
\dfrac{d(\tan(\theta))}{d\theta}
=
\dfrac{d\theta}{\cos^2(\theta)} \cdot \dfrac{1}{d\theta}
=
\dfrac{1}{\cos^2(\theta)}
\]
以上のことからtan(θ)の微分は必ず 1/cos2(θ)になります。
3. 三角関数の微分の面白い性質
ここまで三角関数の微分を見てきましたが、これらには面白い性質があります。実は sin の微分と cos の微分は以下のようにお互いに循環しているのです。
sinの微分の循環性
\[\begin{eqnarray}
\sin^{\prime}(\theta)
&=&
\cos^{\prime}(\theta)\\
\longrightarrow
\cos^{\prime}(\theta)
&=&
-\sin^{\prime}(\theta)\\
\longrightarrow
-\sin^{\prime}(\theta)
&=&
-\cos^{\prime}(\theta)\\
\longrightarrow
-\cos^{\prime}(\theta)
&=&
\sin^{\prime}(\theta)\\
\end{eqnarray}\]
※見切れている場合は右にスクロールすることができます。
ぜひ以下のアニメーションでも視覚的に確認してみてください。
このように \(y=\sin(x)\)、\(y=\cos(x)\) は４回微分すると元に戻ります。この性質を知っておくと、複素数やオイラーの公式などの学習に進んだときに少しだけ有利になりますので、ぜひ覚えておきましょう。
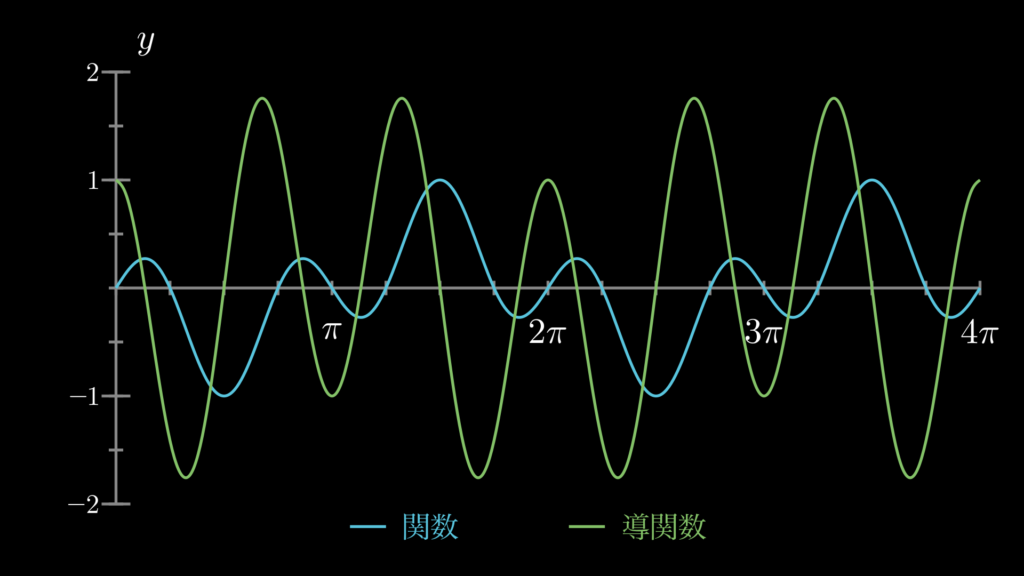
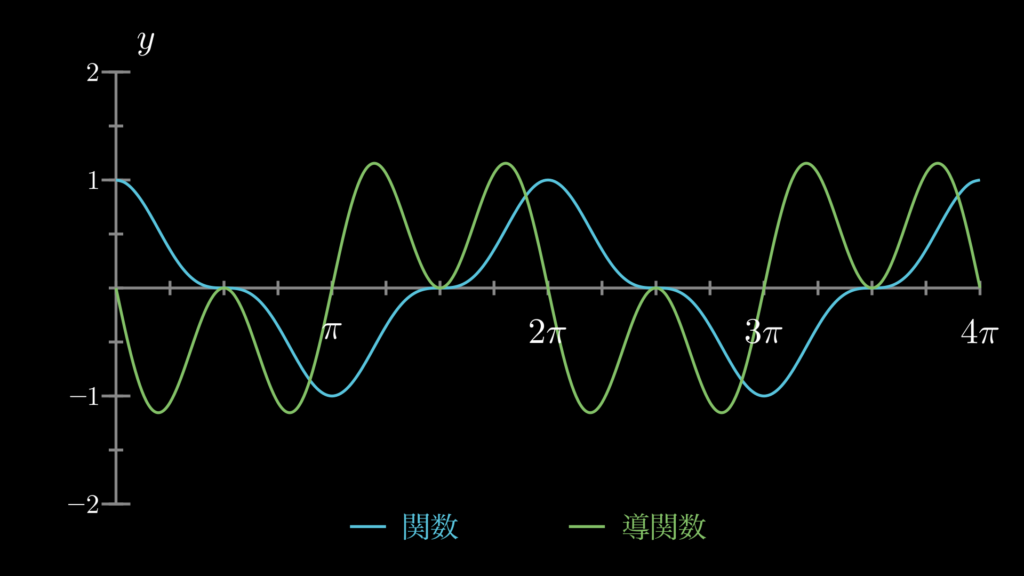
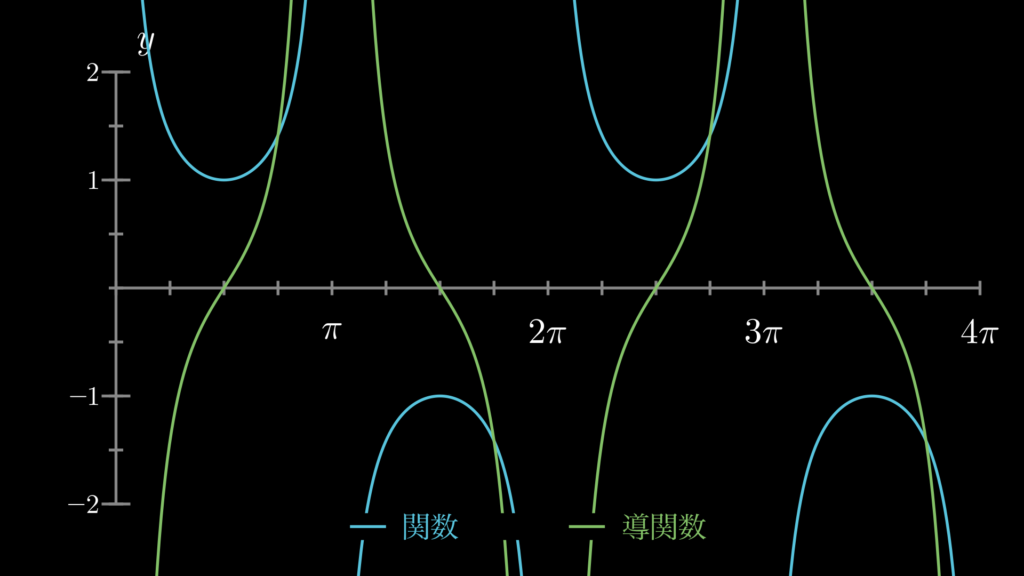
4. 三角関数の微分の練習問題
ここでは、三角関数の微分の理解に役立つ練習問題を用意しています。ぜひチャレンジしてみてください。解答と一緒に、関数と導関数をグラフにしたものも見ることができますので、そちらもぜひご確認ください。
問題：次の関数を微分せよ。
\[
y=2\sin(x)
\]
解答：
これは簡単です。定数倍の微分公式より関数の定数倍の微分は、\(\{\mathrm{c}f(x)\}^{\prime}=\mathrm{c}f^{\prime}(x)\) なので以下の通りになります。
\[
\{2\sin(x)\}^{\prime}=2\sin^{\prime}(x)=2\cos(x)
\]
以下に関数 \(2\sin(x)\)と導関数 \(2\cos(x)\) を描いたグラフを載せておきます。
問題：次の関数を微分せよ。
\[
y=\sin(2x)
\]
解答：
これは関数 \(g(h(x))=\sin(2x)\) という合成関数になっています。そのため合成関数の微分公式で解きます。
次のようになります。
\[\begin{eqnarray}
\{\sin(2x)\}^{\prime}
&=&
\sin^{\prime}(2x)\cdot (2x)^{\prime}\\
&=&
\cos(2x)\cdot 2\\
&=&
2\cos(2x)
\end{eqnarray}\]
以下に、関数 \(\sin(2x)\)と導関数 \(2\cos(2x)\) を描いたグラフを載せておきます。
視覚的には、関数の青い波の感覚が狭くなればなるほど、瞬間の変化率（＝傾き）が大きくなるので、導関数の緑の波が高くなるということを覚えておくとわかりやすいです。
問題：次の関数を微分せよ。
\[
y=\cos(\frac{1}{2}x+2)
\]
解答：
これも合成関数の微分の公式を使って解きます。
\[\begin{eqnarray}
y^{\prime}&=&f^{\prime}(g(x))\cdot g^{\prime}(x)\\
&=&
-\sin(\frac{1}{2}x+2)\cdot \frac{1}{2}\\
&=&
-\frac{1}{2}\sin(\frac{1}{2}x+2)
\end{eqnarray}\]
以下に、関数 \(\cos(\dfrac{1}{2}x+2)\)と導関数 \(-\dfrac{1}{2}\sin(\dfrac{1}{2}x+2)\) を描いたグラフを載せておきます。
問題：次の関数を微分せよ。
\[
y=\frac{1}{2} \tan(\frac{1}{2}x+\pi)
\]
解答：
これは合成関数の微分の公式を使って、以下のように解きます。
\[\begin{eqnarray}
y^{\prime}&=&\dfrac{1}{2}\cdot f^{\prime}(g(x))\cdot g^{\prime}(x)\\
&=&
\dfrac{1}{2}
\cdot
\dfrac{1}{cos^2(\dfrac{1}{2}x+\pi)}
\cdot
\dfrac{1}{2}\\
&=&
\dfrac{1}{4cos^2(\dfrac{1}{2}x+\pi)}
\end{eqnarray}\]
以下に関数と導関数を描いたグラフを載せておきます。
問題：次の関数を微分せよ。
\[
y=\sin(x)\cos(2x)
\]
解答：
これ積の微分法則を使って解きます。次のようになります。
\[\begin{eqnarray}
y^{\prime}&=&f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\\
&=&
\cos(x)\cdot\cos(2x)+\sin(x)\cdot -2\sin(2x)\\
&=&
\cos(x) \cos(2x) – 2\sin(x)\sin(2x)
\end{eqnarray}\]
以下に関数と導関数を描いたグラフを載せておきます。
問題：次の関数を微分せよ。
\[
y=\cos^3(x)
\]
解答：
合成関数の微分公式を使って解きます。
\[\begin{eqnarray}
y^{\prime}
&=&
3\cos^2(x)\cdot -\sin(x)\\
&=&
-3\cos^2(x) \sin(x)
\end{eqnarray}\]
以下に関数と導関数のグラフを載せておきます。
問題：次の関数を微分せよ。
\[
y=\dfrac{1}{\sin(x)}
\]
解答：
『1/xの微分を誰でも簡単に理解できるように解説』で解説しているとおり、これは \(\sin^{-1}(x)\) に変換できますので、解答は以下の通りです。
\[\begin{eqnarray}
\{\sin^{-1}(x)\}^{\prime}
&=&
-1\sin^{-2}(x) \cdot \cos(x)\\
&=&
-\dfrac{1}{\sin^2(x)}\cdot \cos(x)\\
&=&
-\dfrac{\cos(x)}{\sin^2(x)}
\end{eqnarray}\]
以下に関数と導関数のグラフを載せておきます。
5. 三角関数の微分のまとめ
以上が三角関数の微分です。
最初は完全に理解できないところもあるかもしれません。また、練習問題の中には、微分の他の公式を理解していなければ、なかなか難しいものもあります。しかし、当サイトの微分のコンテンツを一つずつご覧いただければ、最終的には驚くほど微分の全てが理解できるようになっていると思います。
ぜひ、引き続きコツコツと微分のコンテンツをご覧頂いて、視覚的に考えてみてください。
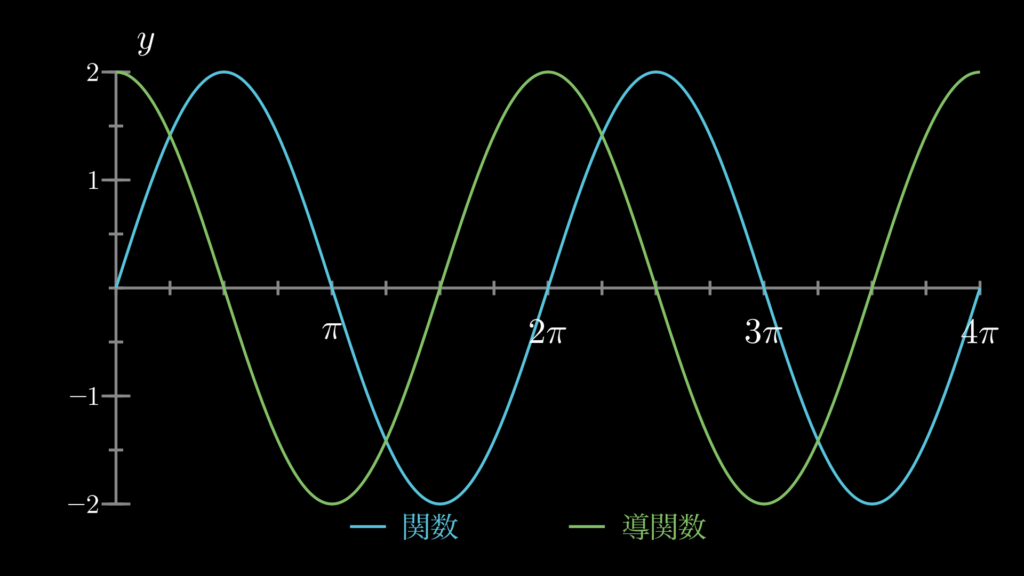
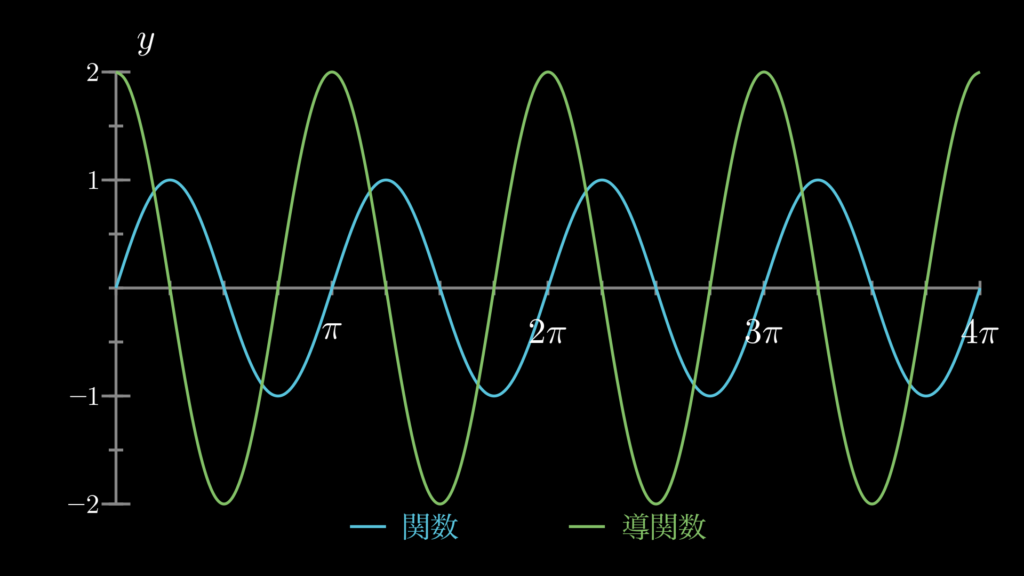
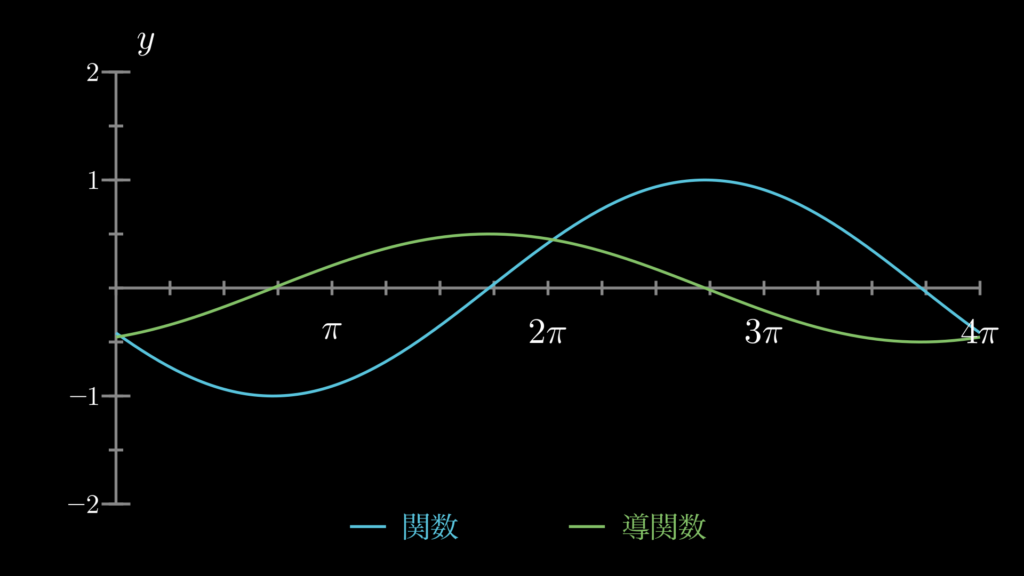
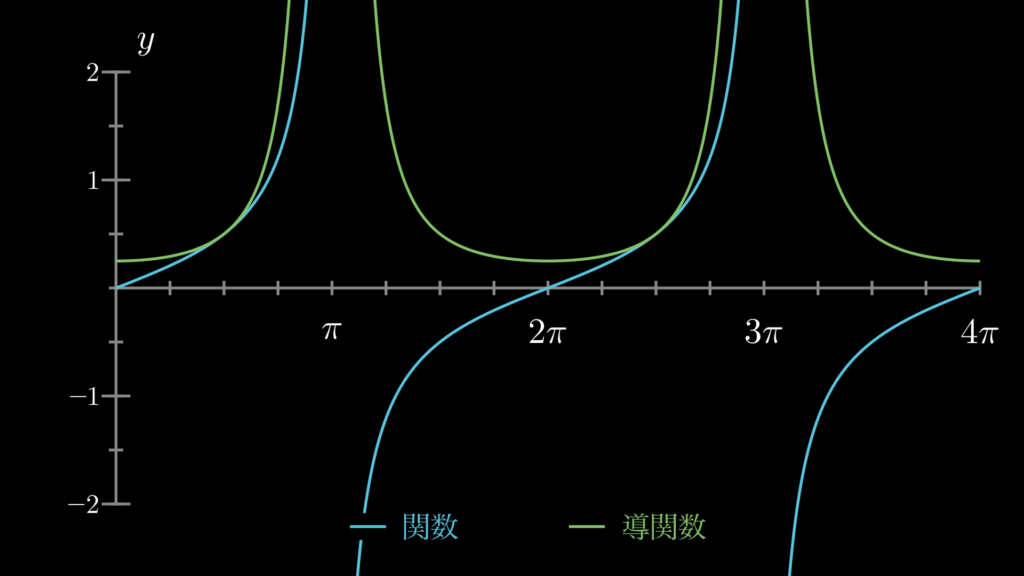
コメントを残す