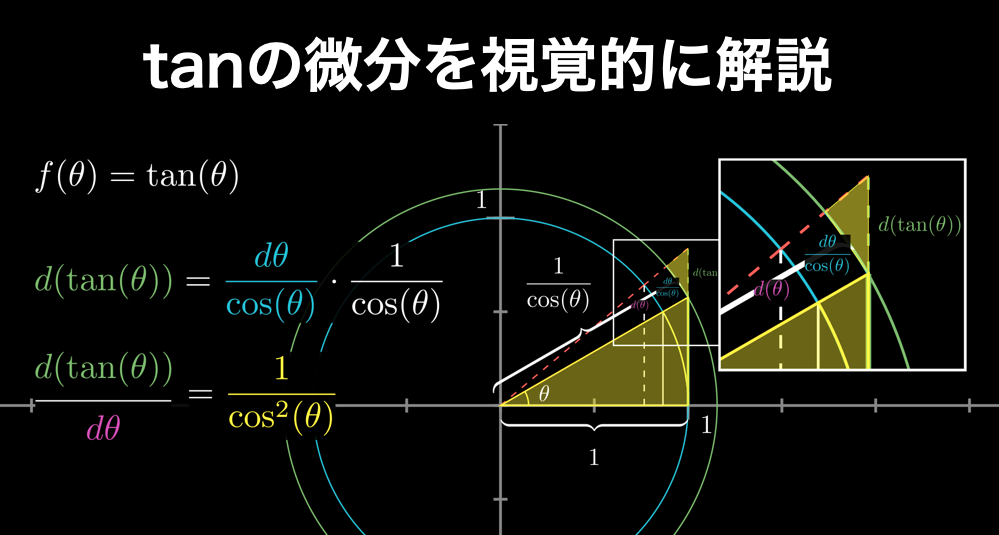
結論からお伝えすると、tan(θ)の微分は1/cos2(θ)になります。
なぜこうなるのでしょうか？その理由がわかると、単に公式を暗記するだけの場合と比べて、遥かに微分を深く理解できるようになります。そこで当ページでは、tanの微分について、誰でも理解できるようにアニメーションを使いながら、詳しく解説していきます。
それでは始めましょう。
1. tanとは
最初にtanについて簡単に復習しておきましょう。
tanとは単位円上にできる、なす角をθとする直角三角形の斜辺の傾きのことです。これは以下のようにsinをcosで割ることで求められます。
tan(タンジェント)の定義
\[\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}\]
なす角がθの直角三角形において、sinは対辺（高さ）であり、cosは隣辺の長さ（底辺の長さ）なので、この計算は斜辺の傾きを求めるものであることがわかります。
そして、tanは視覚的には以下のアニメーションで示しているように底辺の長さが常に1で、斜辺の長さが \(\frac{1}{\cos(\theta)}\)の直角三角形の対辺の長さとしてイメージすることができます。そのためtanの値は、θが 0π (0°)・1π (180°) のときは0になり、1/2π (90°)・3/2π (270°) 付近では無限大または無限小になります。
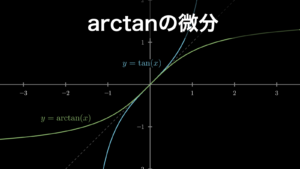
このtanを、横軸がθ・縦軸がtan(θ)のグラフに描いたものが有名なタンジェントカーブ（正接曲線）です。
以上がtanです。
なお、sinとcosについては以下のページで解説していますので、復習したい場合はぜひご確認ください。
2. tanの微分は 1/cos2(θ)
tanの微分公式は次の通りです。
tanの微分公式
\[
\tan^{\prime}(\theta)
=
\frac{1}{cos^2(\theta)}
\]
以下のアニメーションでは、これを視覚的に表しています。青が関数 tan(θ)、緑が導関数 1/cos2(θ) で赤線は各値での微分係数です。
このようにtanの微分は、必ずこの公式の通りになります。それでは、なぜそうなるのでしょうか？次にこれについて考えていきましょう。
3. tanの微分の証明
なぜ、tan(θ)の微分は1/cos2(θ)になるのでしょうか。ただ公式の通りに盲目的に問題を解くのではなく、こうしたことについて深く考えることは、微分の理解を深めるためのとても良い訓練になります。
まず、微分は dy/dx で求められます。そして、三角関数の微分を理解するための鉄則は、単位円上の直角三角形において、このdyとdxが何を意味するのかを考えることにあります。
なお、dxはθの変化であり、dyはθが変化することによるtan(θ)の値の変化です。具体的には tan(θ+dx)-tan(θ) で求められます。これらを、それぞれ dθ・d(tan(θ)) と表すことにします。
念のため、これを以下に示しておきます。
tanの微分の計算方法
\[
\tan^{\prime}(\theta)
=
\dfrac{dy}{dx}
=
\dfrac{\tan(\theta+dx)-\tan(\theta)}{dx}
=
\dfrac{d(\tan(\theta))}{d\theta}
\]
※見切れている場合は右にスクロールすることができます。
さて、それではdθとd(tan(θ))は何を意味しているのでしょうか。これを単位円上の直角三角形で視覚的に確認してみましょう。ぜひ、以下のアニメーションをご覧ください。
このように視覚的に確認すると、d(tan(θ))と d(θ)/cos(θ) が小さな直角三角形を形成していることが見えてきます。そして、この小さな直角三角形をよく見てみると、半径が 1/cos(θ) の元の直角三角形と相似形になっていることがわかります。
以下のアニメーションでご確認ください。
以上のことから、小さな三角形の底辺と斜辺の比率は、大きな三角形の底辺と斜辺の比率である 1 : 1/cos(θ) と同じになることがわかります。そのため、最終的にtanの微分は次のように求めることができるのです。
書き換えた \(d(\tan(\theta))\) を微分式に代入
\[\begin{eqnarray}
\tan^{\prime}(\theta)
=
\dfrac{dy}{dx}
&=&
\dfrac{d(\tan(\theta))}{d\theta}\\
&=&
\dfrac{\frac{d\theta}{\cos^2(\theta)}}{d\theta}\\
&=&
\dfrac{d\theta}{\cos^2(\theta)} \times \dfrac{1}{d\theta}\\
&=&
\dfrac{1}{\cos^{2}(\theta)}
\end{eqnarray}
\]
以上のことから、tanの微分は必ず公式の通りになります。
4. まとめ
いかがだったでしょうか。
tanの微分は、sinやcosと比べて少しトリッキーです。しかし、順番に考えていくと、スッキリと証明できることがわかります。当ページが理解の役に立ったなら、とても嬉しく思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント
コメント一覧 （5件）
突然のメール申し訳ございません。
とても分かりやすく、深い内容のブログで感動しています。
一点、どうしても理解できない部分があり質問させて下さい。
以下の部分ですが、なぜ相似と言えるのでしょうか？
どの角と、どの辺の比が等しいと言えますでしょうか？
d(tan(θ))と d(θ)/cos(θ) が小さな直角三角形を形成していることが見えてきます。そして、この小さな直角三角形をよく見てみると、半径が 1/cos(θ) の元の直角三角形と相似形になっていることがわかります。
※クァンダで質問したのですが、回答できる方がおらずお聞きしました。
恐らく自己解決できました。
円の接線の角が90度
三角形の一つの外角の和は、それに隣り合わない内角の2つの和に等しいことを利用して相似を証明できそうと思います。
すばらしいブログに出会えたことに感謝します。
ひとつ教えてください、小さな直角三角形の底辺がd(θ)/cos(θ)になることが分かりません。
とくにcos(θ)がここにあることが分かりません。
1か月考えましたがだめでした。ここが分かれば後は分かります。
どうか分かりやすく教えてください。お願いします。
70才の老人です。認知症予防のために勉強してます。
半径が1から1/cosθになっているから比例してdθが1/cosθ倍になっているのでは？
御礼の返信が遅くなりまして申し訳ありません。
私のような老人の質問に時間を割いていただき、ありがとうございます。
半径と円周との関係だったのですね。
単純明快な御説明をありがとうございます。
答えがわかってほっとした気持ちです。
私なりに１ケ月以上考えましたので、あなたの回答で、このことに終止符が打たれたことは、
嬉しさと同時に何かに足元をすくわれたような気持ちです。
でも、あなたの文章の終わりに？記号がありましたので私の劣等感も少し和らぎました。
あなたの心配りを感謝します。