積分とは、一言で表すと「ある関数が描く面積」であり「微分と正反対の演算」です。そして積分を理解すると、ある関数の面積を、とても簡単に求められるようになるため、さまざまな分野で非常に重要なものになっています。
そこで、このページでは、積分について、豊富なイメージやアニメーションを使って丁寧に解説していきます。そして、なぜ積分で面積を求めることができるのか、なぜ積分は微分の反対なのか、という点についても誰でも理解できるように解説します。
しっかりとご覧頂ければ、積分の学習が初めてという方でも、以前学んだけれどもイマイチ理解に不安があるという方でも、必ず積分を深く理解できるようになります。
ぜひ参考にして頂ければと思います。それでは早速始めましょう。
1. 積分とは何か
冒頭でも述べた通り、結論から言えば、積分とは
- ある関数が描く面積
- 微分と正反対の演算
です。それぞれ詳しく見ていきましょう。
1.1. 積分は面積
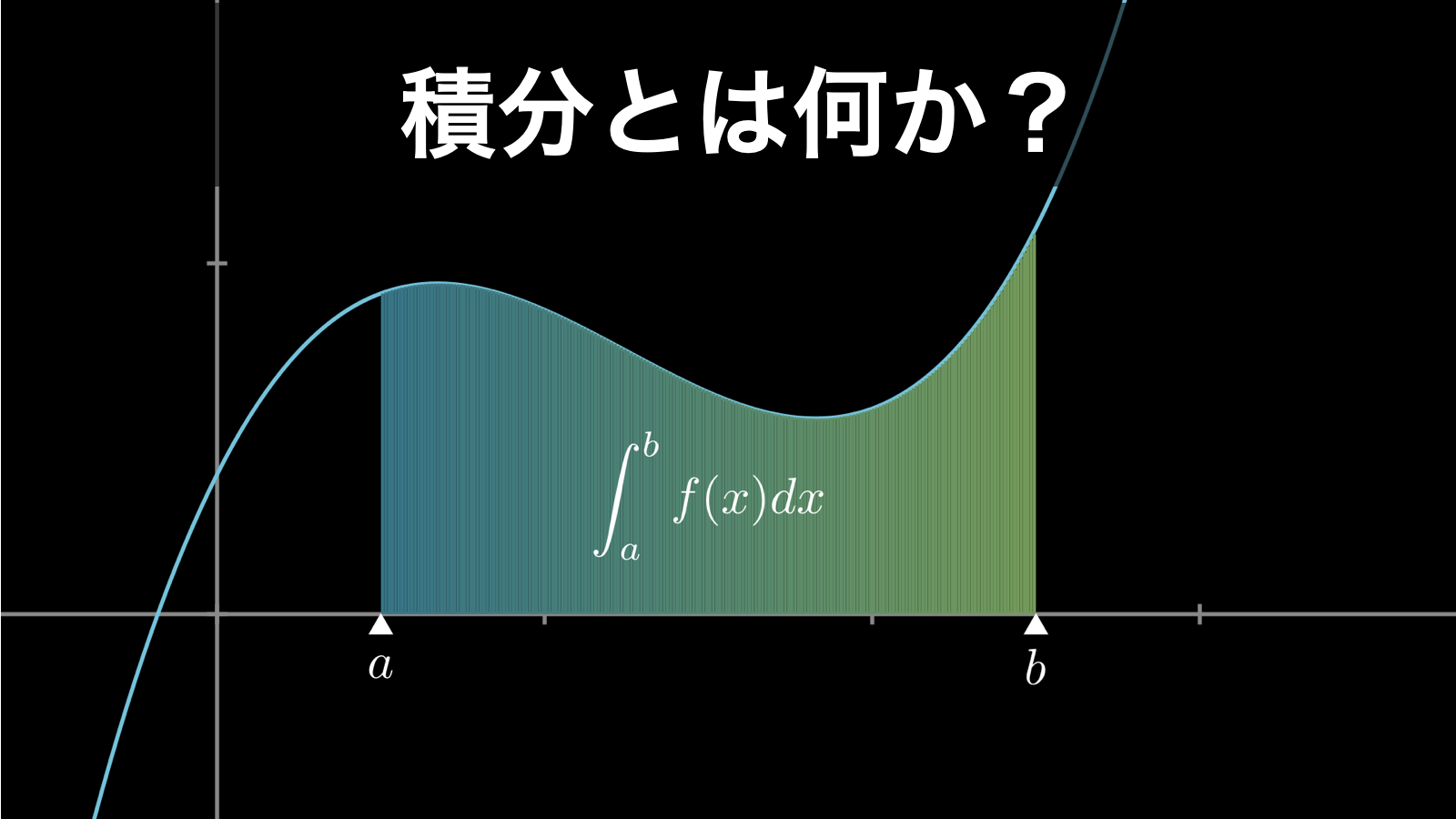
以下の画像をご覧ください。これは関数 \(f(x)\) の [\(a,b\)] 間における積分(=\(f(x)\) と \(x\) 軸に囲まれた部分の面積)を示したものです。
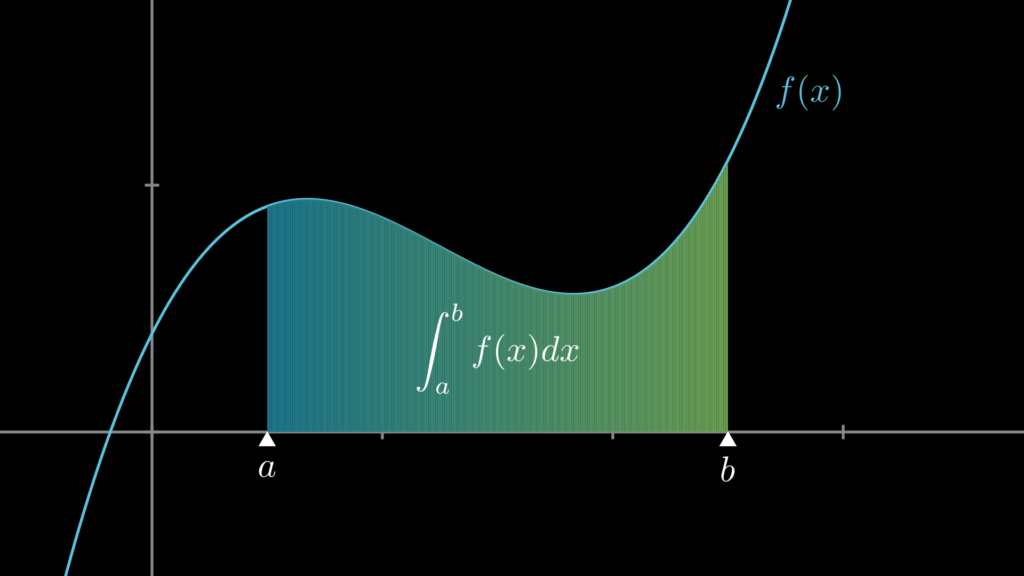
この面積が関数 \(f(x)\) の積分です。そして、この積分は記号を使って次のように表します。
関数 \(f(x)\) の [\(a,b\)] 間の面積(積分)を表す記号
\[\int^{b}_{a}f(x)dx\]
記号の詳しい見方については後ほど改めて解説します。ここでは、まず「積分とは面積である」ということをしっかりと頭に入れておきましょう。また、面積の値は \(x\) 軸より上の部分は正の値、下の部分は負の値になるという点も覚えておいてください。
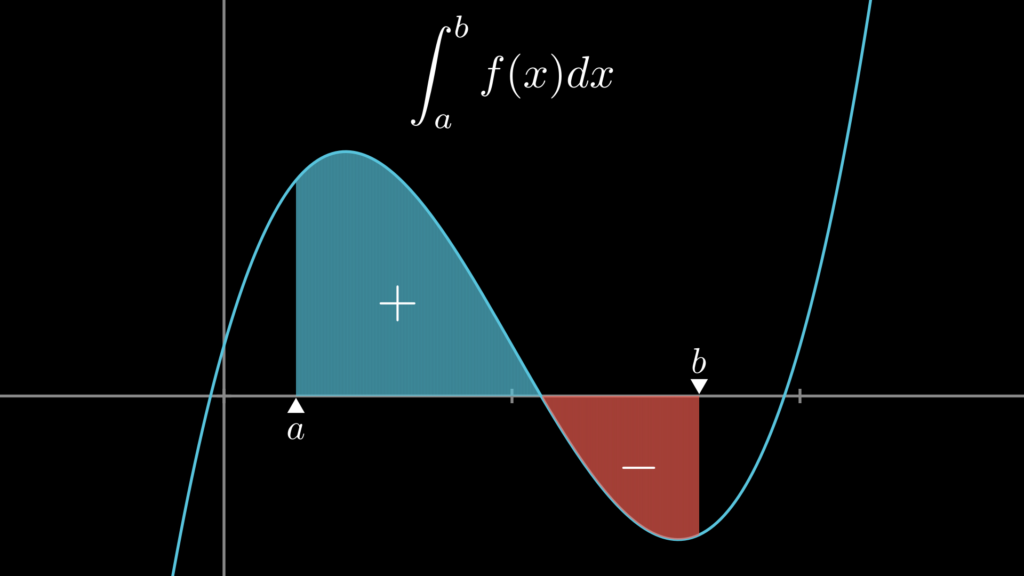
積分が分かると、あらゆる関数の任意の [\(a,b\)] 間の面積を簡単に求められるようになります。それでは、積分はどのように求められるのでしょうか。これは、「微分正反対の演算」で求めることができます。
1.2. 積分は微分の反対
積分には、「面積である」という点に加えて、もう一つ「微分と全く正反対の演算である」という重要な性質があります。要するに、微分をすると\(f(x)\) になるような関数 \(F(x)\) が積分であるということです。
\[\begin{eqnarray}
f(x) \ \
&\overset{\text{積分}}{\underset{\text{微分}}{\rightleftarrows}}&
\ \ F(x)
\end{eqnarray}\]
たとえば \(x^2\) を微分すると \(2x\) になります。そして \(2x\) を積分すると \(x^2\) になります。そのため、\(f(x)=2x, \ \ F(x)=x^2\) です。そして、このように \(f(x)\) の積分 \(F(x)\) がわかっているとき、関数 \(f(x)\) の [\(a,b\)] 間の面積は、以下の公式によって簡単に求めることができます。
微分積分学の基本定理
\[\begin{eqnarray}
\int^{b}_{a}f(x)dx=F(b)-F(a)
\end{eqnarray}\]
実は、これは「微分積分学の基本定理」と言って、数学の飛躍的な発展に貢献した重要な定理の一つです。
例として、関数 \(f(x)=2x\) の [\(2,5\)] 間の面積 \(\int^{5}_{2}f(x)dx\) を求めてみましょう。すでに見た通り、\(f(x)=2x\) のとき、\(F(x)=x^2\) なので、この面積は次の計算で求めることができます。
\(f(x)=2x, \ F(x)=x^2\) の場合
\[\begin{eqnarray}
\int^{5}_{2}f(x)dx&=&F(5)-F(2)\\
&=& 5^2-2^2\\
&=& 21
\end{eqnarray}\]
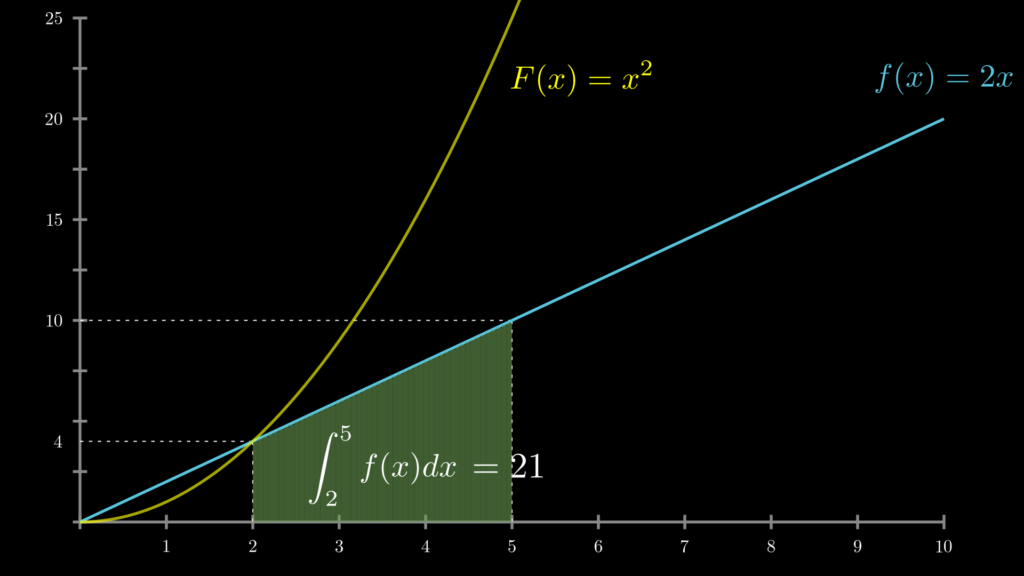
以上が積分(面積)の求め方です。なぜ、この「微分積分学の基本定理」で面積を求められるのかについては、後ほど、なぜ積分と微分は正反対の演算なのか、のところで解説します。
1.3. 定積分と不定積分
さて、ここまで積分を表す記号として、\(\int^{b}_{a}f(x)dx\) と \(F(x)\) の2種類が出てきました。これらはどちらも積分ですが、厳密には前者を「定積分」、後者を「不定積分」と言います。
\[\begin{eqnarray}
\text{定積分}&:& \hspace{2mm} \int^{b}_{a}f(x)dx
\hspace{9mm}
\text{不定積分}&:& \hspace{2mm} F(x)
\end{eqnarray}\]
わかりやすく解説しておきましょう。
定積分とは、「任意の範囲の面積の値そのもの」のことです。上の例では、関数 \(f(x)=2x\) の [\(2,5\)] 間の面積は、\(F(5)-F(2)=21\) でした。同じように [\(0,2\)] 間の面積は、\(F(2)-F(0)=4\) となります。このように「面積の値が定まっているもの」が定積分です。
一方で、不定積分とは「 \(f(x)\) に対する \(F(x)\) 」のことです。\(F(x)\) は、\(f(x)\) の面積を計算するための関数ですが、これだけでは下端の \(a\) と 上端の \(b\) が定まっていないので、「微分積分学の基本定理」によって面積を計算することはできません。つまり、面積が特定の値に定まっていないもの(関数の状態のもの)が、不定積分です。
以上が積分です。
それでは、なぜ積分とは面積なのでしょうか、そしてなぜ積分は微分と正反対の演算であるということになるのでしょうか。これらの点を理解して初めて、積分を理解できたということになります。そこで次から、これらの点について考えていきましょう。
ポイント
- 積分とは「面積」であり、「微分の正反対の演算」である。
- \(\int^{b}_{a}f(x)dx\) を「定積分」という。
- \(f(x)\) に対して \(F(x)\) を「不定積分」という。
- 実際の面積は「微分積分学の基本定理」 \(\int^{b}_{a}f(x)dx=F(b)-F(a)\) で求められる。
2. なぜ積分は面積なのか
ここでは、なぜ積分は面積と等しいのかという点を考えていきます。
これについて考えるには、前提として微分についての理解が必要になります。そのため、不安な場合は、ぜひ『微分とは何か?誰でもわかりやすく理解できるようにイメージで解説』を確認しておいてください。
さて、微分は、言ってみれば距離の関数から速度の関数を導き出すものだと考えることができました。つまり、時間によって移動距離がどう変化するかを見て、各時点での速度を計算するというものです。
一方で積分は、微分とは反対に、速度の関数から距離の関数を導き出すものです。つまり、各時点での速度の変化を見て、全体の移動距離を計算するというものです。これは、「速度計だけを見て移動距離を求める」という状況をイメージするとわかりやすくなります。
2.1. 速度計だけを見て移動距離を求める
次のような状況を考えてみてください。
あなたは車に乗っています。ただし、車の窓ガラスにはスモークがかかっており、外の景色を確認することはできません。見えるのは速度計だけです。そして、この速度計の針は以下のアニメーションで示しているように変化しています。
このときに移動距離を知るにはどうすれば良いでしょうか。
このような問題を考えるときは、まず最初にグラフ化が必要です。そこで速度計の値を、縦軸が速度(\(\mathrm{m}/\mathrm{s}\))・横軸が時間(秒)のグラフにプロットしてみましょう。すると、以下のような速度関数 \(v(t)=t(10-t)\) が現れます。
さて、この速度関数から移動距離(距離関数)を求めるには、どうすれば良いでしょうか?
2.2. 速度関数では移動距離=面積
結論から言うと、速度関数においては、移動距離は曲線下の面積と等しくなります。そのため、移動距離を求めるには面積を求めれば良いということになります。
「距離が面積に等しい」と言うと直感に反するかもしれません。しかし、このことは \(v(t)=10\) のように、速度が常に一定の関数を考えると、とても分かりやすくなります。
まず、\(v(t)=10\) をグラフに描くと以下のようになります。
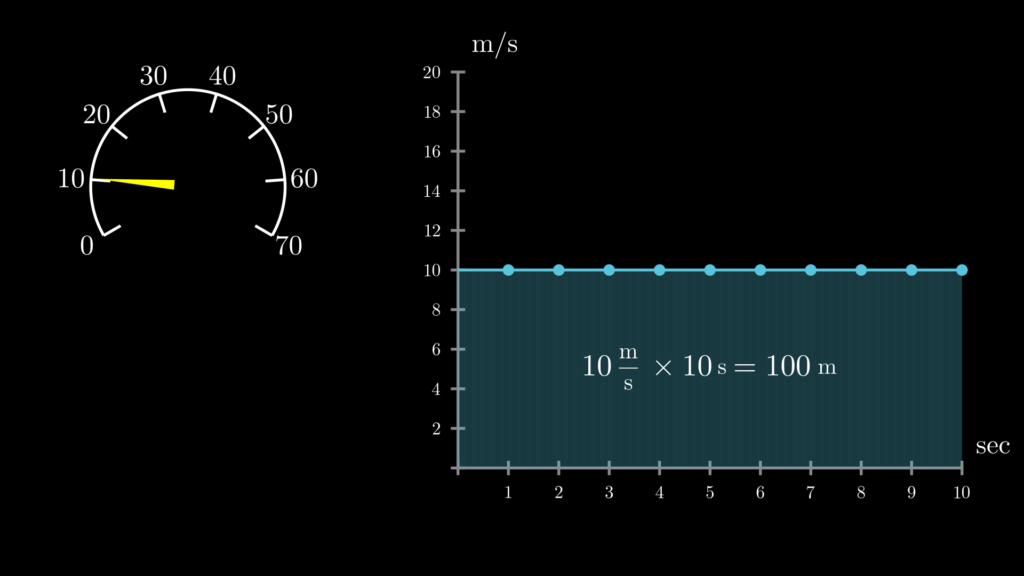
速度関数では、縦軸の単位が速度 \(\frac{\mathrm{m}}{\mathrm{s}}\) で、横軸の単位が時間 \(\mathrm{s}\) なので、移動距離は縦軸×横軸で求められることになります(\(\frac{\mathrm{m}}{\mathrm{s}}\times \mathrm{s}=\mathrm{m}\))。
このように速度関数においては「移動距離=面積」となります。そして積分とは、この面積を求めるためのツールなのです。
そして、ご覧の通り面積が長方形の場合、計算はとても簡単です。しかし、先ほどのアニメーションのように、連続的に加速・減速しているような場合(グラフが複雑なカーブを描いている場合)は、計算が一気に難しくなります。そのような場合は、どのようにしたら正確な面積(移動距離)を計算することができるのでしょうか。
2.3. 曲線下の面積をどう求めるか
さて、曲線下の面積を正確に求めるにはどうしたら良いのでしょうか。まずは大まかに当たりをつけてみることから始めてみましょう。
例えば、\(1\) 秒ごとの速度を確認すれば、各秒間の大まかな移動距離を把握することができそうです。そこで以下の画像で示しているように、\(0\) 秒時点での速度は \(0 \frac{\mathrm{m}}{\mathrm{s}}\) なので、 \(0 \sim 1\) 秒間の移動距離は \(0 \frac{\mathrm{m}}{\mathrm{s}} \times 1\mathrm{s}=0\mathrm{m}\) だろうと考えることにします。そして \(1\) 秒時点での速度は \(9 \frac{\mathrm{m}}{\mathrm{s}}\) なので、\(1 \sim 2\) 秒間の移動距離は大体 \(9 \frac{\mathrm{m}}{\mathrm{s}} \times 1\mathrm{s}=9\mathrm{m}\) だろうと考えることにします。
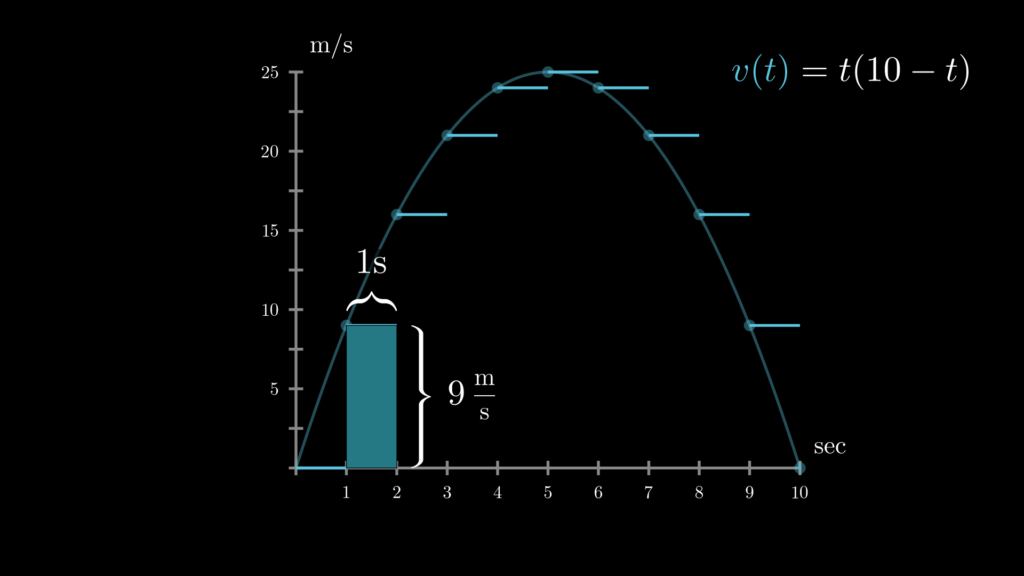
同じようにして、\(2 \sim 3\) 秒間の移動距離は \(16\mathrm{m}\) 、\(3 \sim 4\) 秒間の移動距離は \(21\mathrm{m}\) 、\(4 \sim 5\) 秒間の移動距離は \(\cdots\) 、というように考えることにします。このようにして、それぞれの秒間における大まかな移動距離を足し合わせていくと、以下のように、面積に近い値である \(165\) が得られます。
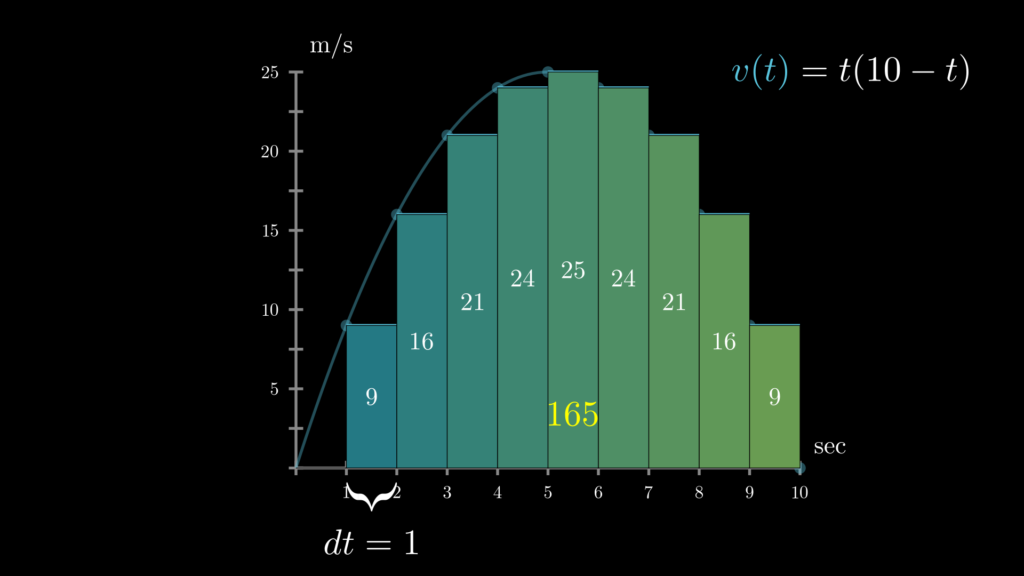
計算式
\[\begin{eqnarray}
\text{面積}
&=&
\sum_{k=1}^{10} v(k)\cdot dt\\
&=&
v(1) \cdot 1\mathrm{s} + v(2) \cdot 1 \mathrm{s} + \cdots + v(10) \cdot 1 \mathrm{s} \\
&=&
9+16+ \cdots + 0\\
&=&
165
\end{eqnarray}\]
※ \(v(t)=t(10-t)\), \(dt=1\)
\(dt\) は “difference in time(時間間隔)” のこと。ここでは間隔は1秒。
この値は実際の面積に結構近いものになっていそうです。しかし、まだ実際の曲線と長方形の間に大きな乖離が見られます。そのため、この値は正確とは言えません。そこで間隔を \(dt=1\mathrm{s}\) からもっと狭めていってみましょう。
例えば、\(dt=0.5\mathrm{s}\) にしてみると、以下のようになります。
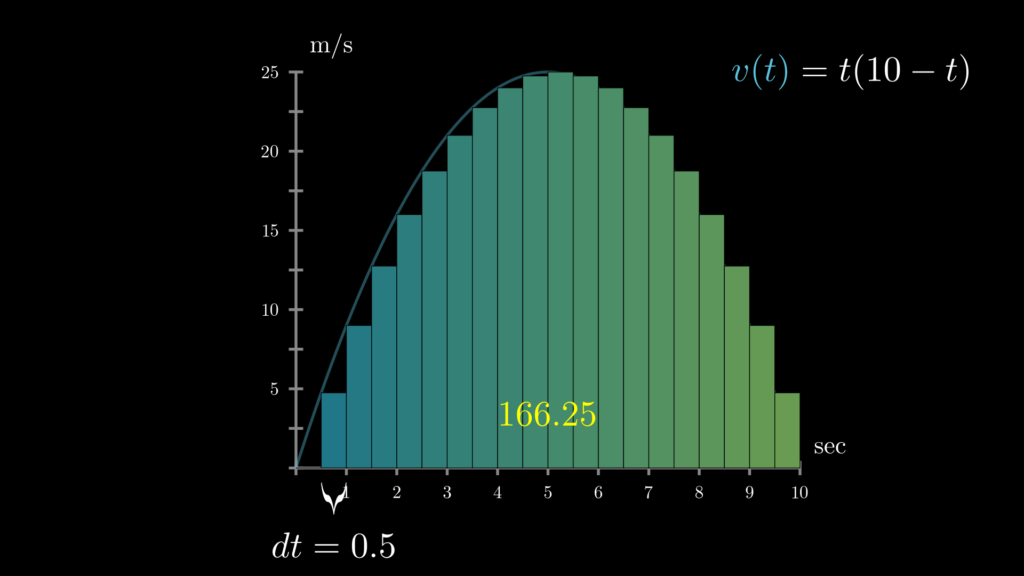
計算式
\[\begin{eqnarray}
\text{面積}
&=&
\sum_{k=1}^{20} v(0.5k)\cdot dt\\
&=&
v(0.5) \cdot 0.5\mathrm{s} + v(1) \cdot 0.5 \mathrm{s} + \cdots + v(10) \cdot 0.5 \mathrm{s} \\
&=&
2.375+4.5+ \cdots + 0\\
&=&
166.25
\end{eqnarray}\]
※ \(v(t)=t(10-t)\), \(dt=0.5\)
いかがでしょうか。視覚的に確認してみると、実際の曲線とのギャップがかなり小さくなり、実際の面積にさらに近づいたことがわかります。
続いて、もっと細かく\(dt=0.1\mathrm{s}\) にしてみると次のようになります。
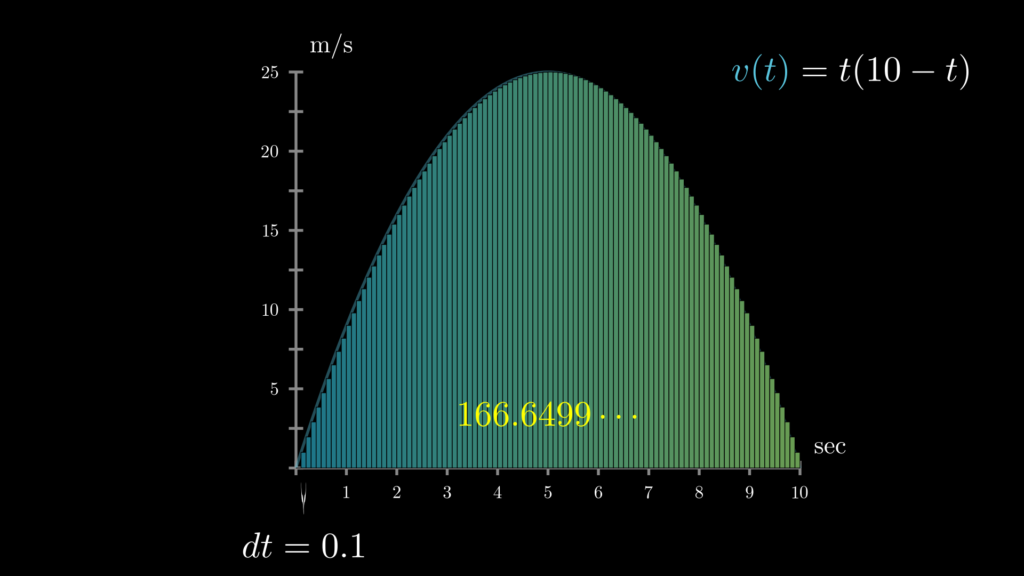
計算式
\[\begin{eqnarray}
\text{面積}
&=&
\sum_{k=1}^{100} v(0.1k)\cdot dt\\
&=&
v(0.1) \cdot 0.1\mathrm{s} + v(0.2) \cdot 0.1 \mathrm{s} + \cdots + v(10) \cdot 0.1 \mathrm{s} \\
&=&
0.099+0.196+ \cdots + 0\\
&=&
166.64999\cdots
\end{eqnarray}\]
※ \(v(t)=t(10-t)\), \(dt=0.1\)
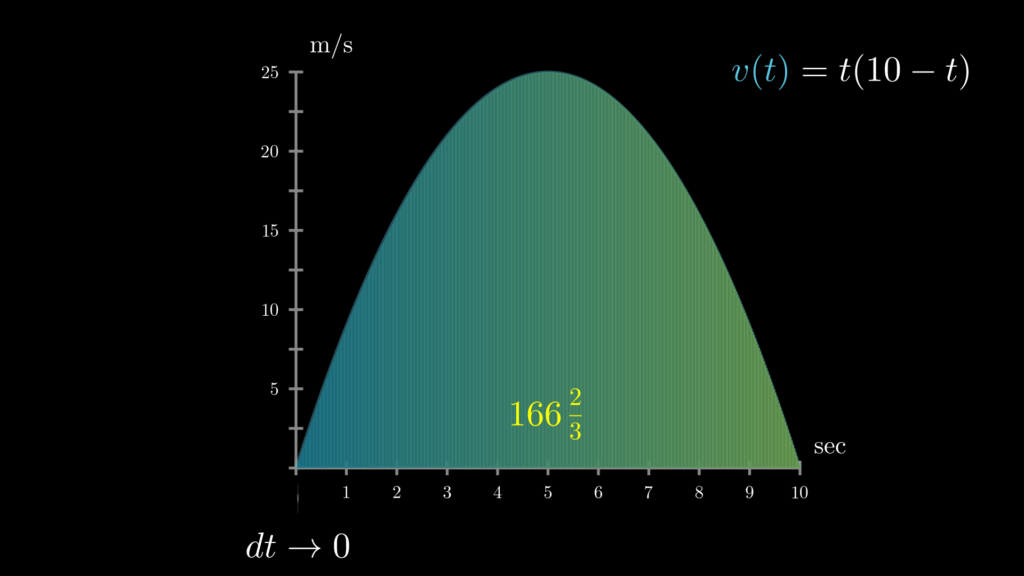
ご覧のように間隔(\(dt\))を狭める度に、長方形の面積の合計が、実際の面積の値にどんどん近づいていることがわかります。ということは、間隔(\(dt\))が限りなくゼロ(=瞬間)に近いとき、長方形の面積の合計は、実際の面積とほとんど同じであるということがわかります。
そして、実際に \(dt\) をゼロにしていくと、値は \(166\frac{2}{3}\) に収束していくことがわかります。
計算式
\[\begin{eqnarray}
\text{面積}
&=&
\sum_{k=1}^{100\cdots 00} v(0.00\cdots 01k)\cdot dt\\
&=&
v(0.00\cdots 01) \cdot 0.00\cdots 01 \mathrm{s} + v(0.00\cdots 02) \cdot 0.00\cdots 01 \mathrm{s} + \cdots + v(10) \cdot 0.00\cdots 01 \mathrm{s} \\
&=&
166.6666\cdots\\
&\approx&
166 \frac{2}{3}
\end{eqnarray}\]
※ \(v(t)=t(10-t)\), \(dt \rightarrow 0\)
この収束値こそが、速度関数に囲まれた部分の実際の面積です。
まとめると実際の面積(=積分)は、間隔 (\(dt\))を限りなくゼロに近くして、一つずつの長方形の面積を足し合わせることで求められるのです。このことから積分という概念は「非常に小さな長方形の面積の集まりを足し合わせることで、物事の全体像をつかむことである」と言い表すことができます。
しかし、いちいち上のような計算式を \(\Sigma\) 記号で示すのは少々面倒です。そこで、これを簡略化して表せられるようにしたものが既に見た \(\int\) 記号です。
積分記号
\[\begin{eqnarray}
\int^{10}_0 v(t)dt
\end{eqnarray}\]
\(dt \rightarrow 0\)
まず、”\(\int^{b}_a\)” 記号は「インテグラル(統合)」と言います。小さな長方形を足し合わせる(=統合する)ことから、こう名付けられています。また、Sを縦に引き伸ばしたような形になっているのは、英語で「合計」を意味する “Sum” の頭文字に由来していると言われています。
続いて \(a, b\) はそれぞれ \(t\) の下端値と上端値を表しています。たとえば、\(\int^{4}_1f(x)dx\) の場合は、以下のように、 \(t=1\) 時点から \(t=4\) 時点までの面積を表していることになります。
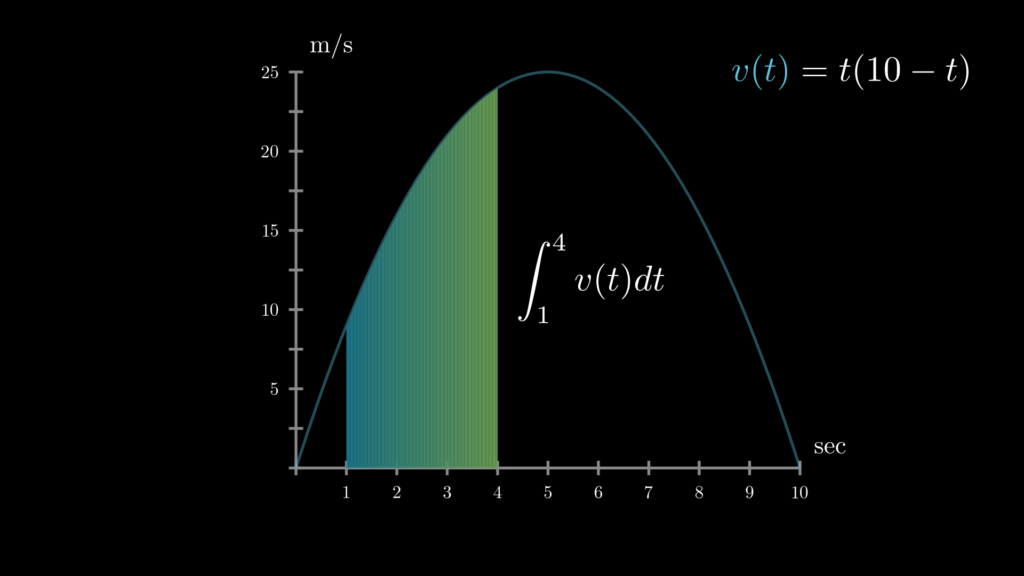
以上が積分です。
ポイント
- 積分(面積)は底辺 \(dt\) が非常に小さい無数の長方形を足し合わせることで求められる。このように、「無数の小さな部分を足し合わせることで全体像を掴む」という概念が積分である。
2.4. 微分積分学の基本定理
それでは \(\int^{4}_1f(x)dx\) の値を実際に求めてみましょう。
どうすれば求められるでしょうか。まずは前段階として、以下のように積分の下端値が \(0\) で、上端値が変数 \(T\) である場合を考えてみてください。
\(t\) の上端を変数 \(T\) に
\[\begin{eqnarray}
\int^{T}_0 v(t)dt
\end{eqnarray}\]
\(v(t)=t(10-t)\)
この式は、車が発進してから \(T\) 秒後の移動距離を表しています。 \(T\) は秒数を表す変数なので、その値が変わると移動距離も変わります。つまり、この式は速度関数 \(v(t)\)に対する距離関数 \(s(T)\) を意味していることになります。
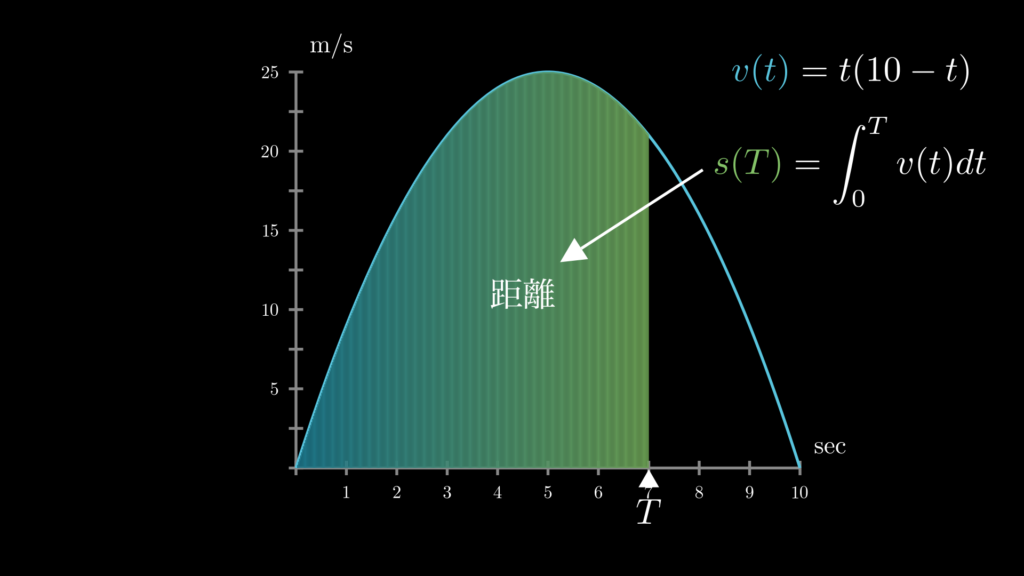
それでは、この距離関数 \(s(T)\) の微分 \(\frac{ds}{dT}\) はどうなるでしょうか。
まず \(dT\) は限りなくゼロに近い時間の変化のことです。そして、\(ds\) は時間が \(dT\) 秒間経過したときの距離の変化です。つまり、\(\frac{ds}{dT}\) は、距離 \(\mathrm{m}\) を時間 \(\mathrm{s}\) で割っていることになるので速度 \(v(t)\) であることになります。
これは以下の画像で視覚的に確認するとわかりやすいでしょう。
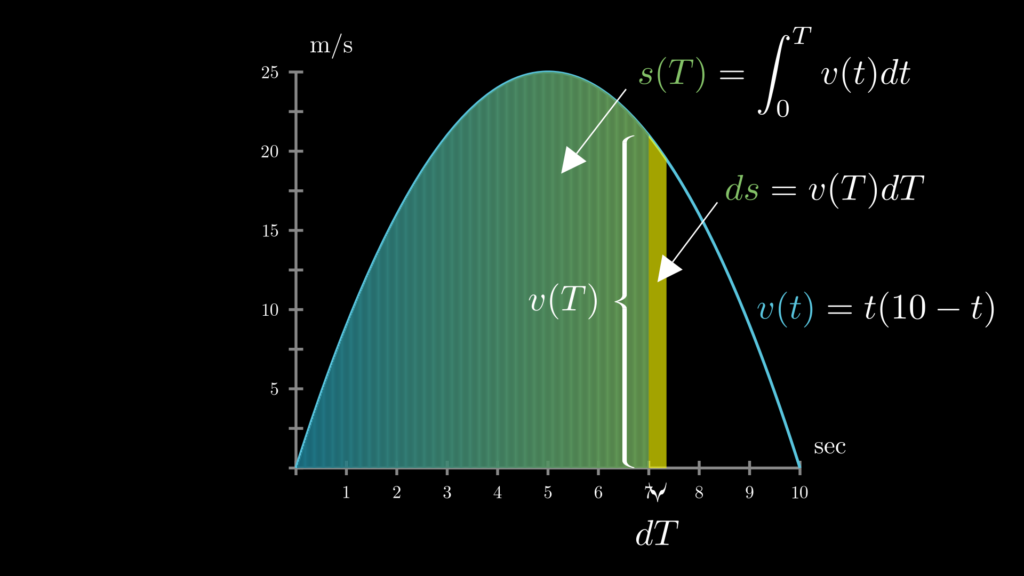
この通り、速度関数 \(v(t)\) において、移動距離は面積に等しいため、時間が \(dT\) 秒経過したことによる距離の変化は、黄色の部分の面積 \(ds=v(T)dT\) と等しくなります。
なお、図中では大きく見せていますが、実際には \(dT\) は限りなくゼロに近い間隔に過ぎません。そのため \(ds\) (黄色の面積)は実際は長方形と考えて問題なくなるので、\(ds=v(t)dT\) で計算することができます(この点について、ピンとこない場合は「微分とは何か?」を読み返しましょう)。そして \(ds=v(t)dT\) なのですから、\(s(t)\) の微分は \(\frac{ds}{dT}=v(t)\) となります。
以上のことから \(v(t)\) と \(s(t)\) はお互いに微分積分の関係になっていることがわかります。
\[\begin{eqnarray}
s(t)
\hspace{5mm}
\overset{\textrm{積分}}{\underset{\textrm{微分}}{\rightleftarrows}}
\hspace{5mm}
v(t)
\end{eqnarray}\]
さて、それでは、ここまで用いてきた速度関数 \(v(t)=t(10-t)\) を積分した距離関数 \(s(t)\) は、具体的には、どのような式で表せるでしょうか。
そう、速度関数は距離関数を微分したものなので、微分をすると \(t(10-t)\) になるような関数を求めれば良いのです。これは \(10t-t^2\) と展開すると求めやすくなります。そして答えを言うと、微分をすると \(10t-t^2\) になるような関数は \(5x^2-\frac{1}{3}t^3\) です。
\[\begin{eqnarray}
s(t)=5t^2-\frac{1}{3}t^3 \
\hspace{5mm}
&\overset{\text{微分}}{\underset{\text{積分}}{\rightleftarrows}}&
\hspace{5mm}
\ v(t)=t(10-t)
\end{eqnarray}\]
さて、このように関数 \(v(t)\)を積分した関数 \(s(t)\) が得られると、任意の範囲の面積は、とても簡単に計算できるようになります。\(s(a)\) は [\(0,a\)] 区間の面積であり、\(s(T)\) は [\(0,T\)] 区間の面積なので、[\(a,T\)] 区間の面積は以下のように計算すれば良いのです。
ある関数を積分した関数を得られると、任意の範囲の面積を簡単に計算できる
\[\begin{eqnarray}
\int^{T}_a v(t)dt
=
s(T)-s(a)
\end{eqnarray}\]
\(v(t)=t(10-t), \ \ s(t)=5t^2-\frac{1}{3}t^3\)
このことから、\(t=1 \sim 4\) の面積は次のように計算できます。
\[\begin{eqnarray}
\int^{4}_1 v(t)dt
&=&
s(4)-s(1)\\
&=&
\left(
5(4)^2-\frac{1}{3}(4)^3
\right)
–
\left(
5(1)^2-\frac{1}{3}(1)^3
\right)\\
&=&
54
\end{eqnarray}\]
\(v(t)=t(10-t), \ \ s(t)=5t^2-\frac{1}{3}t^3\)
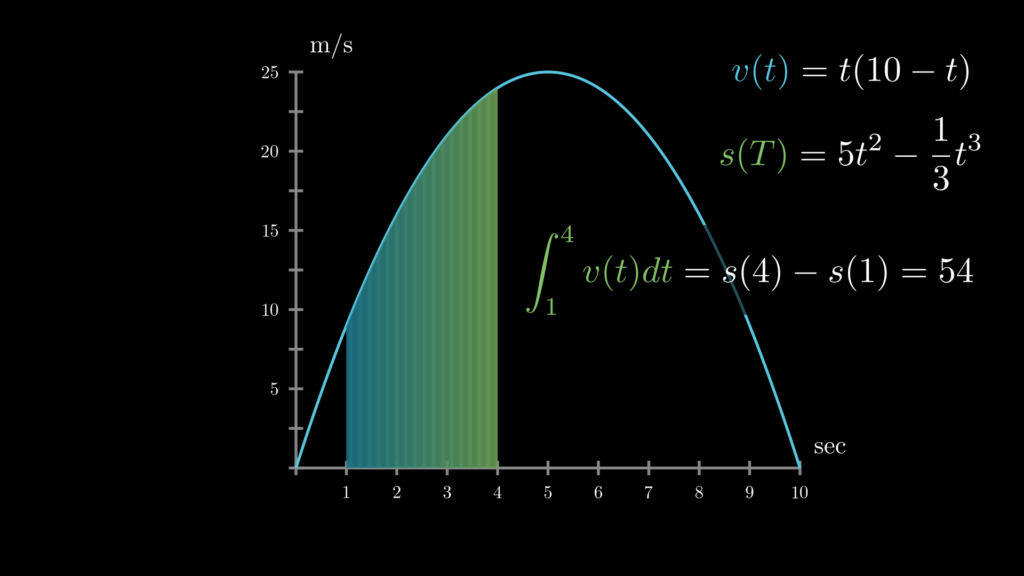
これは、どのような関数に対しても当てはまります。そのため前述したように、これは「微分積分学の基本定理」と呼ばれており、以下のように表されます。\(f(x)\) の積分が \(F(x)\) です。
微分積分の基本定理
\[\begin{eqnarray}
\int^b_a f(x)dx=F(b)-F(a)
\end{eqnarray}\]
※ \(f(x)\) の積分が \(F(x)\)
このように積分ができるようになると、どれだけ複雑な関数だとしても、その面積の計算が非常に簡単になります。
それでは、なぜ積分は微分と正反対の演算で求めることができるのでしょうか。これについては、ここまでで既に説明されているのですが、更に深く理解できるように、改めて別視点から詳しく解説したいと思います。
3. なぜ積分と微分は正反対の演算なのか
なぜ積分(=面積を求めること)と微分(=接線を求めること)は正反対の関係にあるのでしょうか。
結論から言うと、以下の画像で示しているように、積分とは長方形の面積を求めるための「掛け算(高さ×底辺)」であり、微分とは長方形の面積から高さを求めるための「割り算(面積÷底辺)」であるからです。つまり、両者は、掛け算・割り算という対の関係になっているのです。
これが、積分と微分は正反対の計算であるということの本質的な意味です。
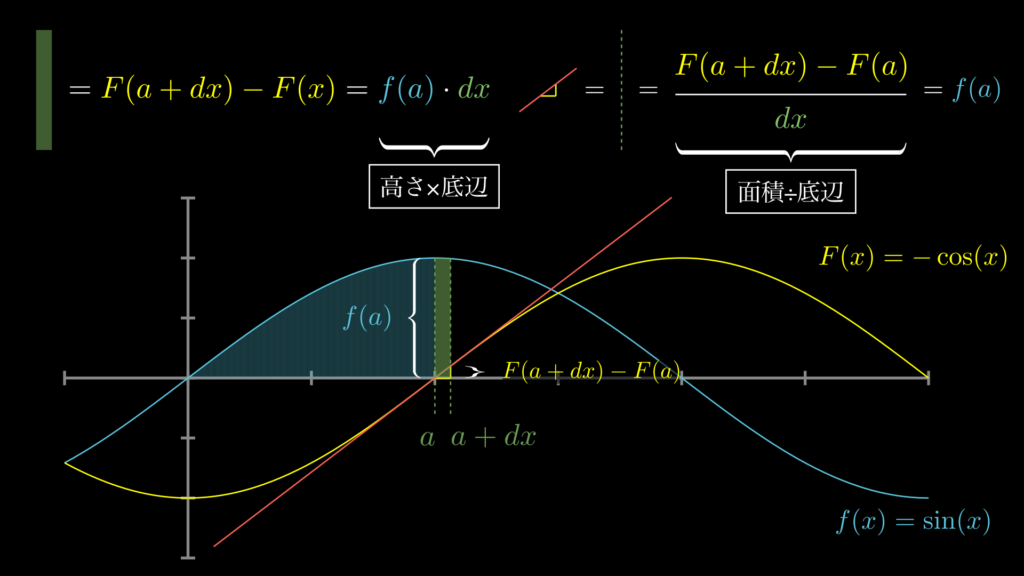
これから、この点について誰でも視覚的(直感的)に理解できるように解説していきます。なお解説には以下の関数を使います。
\[\begin{eqnarray}
f(x)=\sin(x)
\hspace{5mm}
\overset{\textrm{積分}}{\underset{\textrm{微分}}{\rightleftarrows}}
\hspace{5mm}
F(x)=-\cos(x)
\end{eqnarray}\]
ポイント
積分と微分が「正反対の関係」であるということは、具体的には、「積分=長方形の面積を求めるための掛け算」・「微分=長方形の面積から高さを求めるための割り算」という対の関係になっているということを意味する。
3.1. 積分は面積を求める掛け算(高さ×底辺)
まず、\(f(x)=\sin(x)\) の積分(面積)を見ていきましょう。
ここまで見てきた通り、関数 \(f(x)\) の [\(a, \ a+dx\)] 間の面積は \(F(a+dx)-F(a)\) で求められます。そして下図で視覚的に確認してみると、この面積(下図の緑の長方形の部分)は、「高さ×底辺(\(=f(a) \cdot dx\))」 でも求められることがわかります。
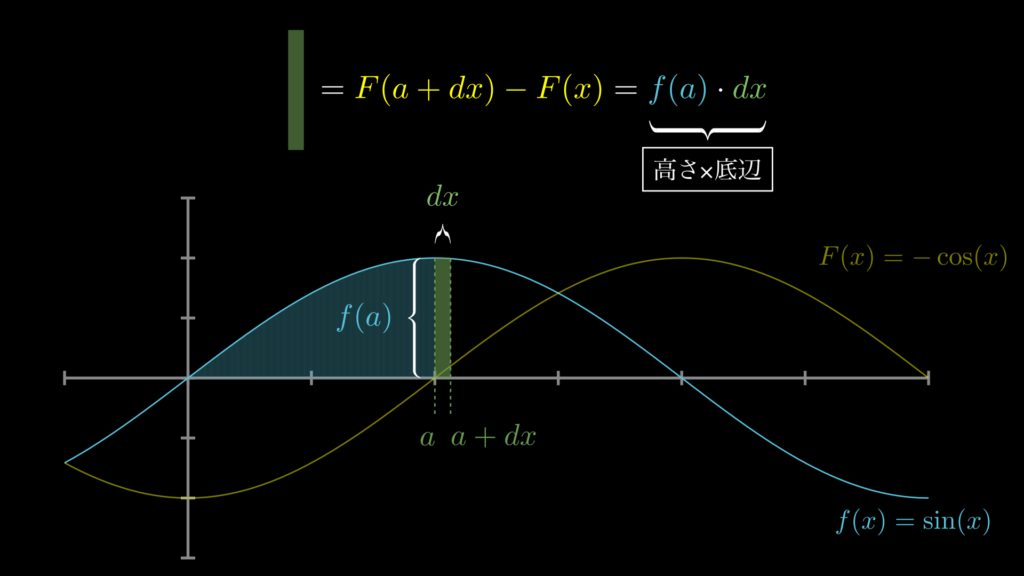
もちろん、この緑の部分は曲線下にあるので、純粋な長方形ではありません。しかし、\(dx\) は限りなくゼロに近い値であるため、実用上は長方形であると考えて構いません(これについては「微分とは何か?」で詳しく解説しています)。
このように \(\underset{dx \rightarrow 0}{\lim}\) のとき(\(dx\) が限りなく\(0\) に近い値であるとき)、あらゆる関数 \(f(x)\) の、 [\(a, \ a+dx\)] 区間における面積 \(F(a+dx)-F(a)\) は、 高さと底辺の掛け算 \(f(a) \cdot dx\) で求められるのです。
\(\underset{dx \rightarrow 0}{\lim}\) のときの [\(a, \ a+dx\)] 区間における \(f(x)\) 下の面積
\[\begin{eqnarray}
\int^{a+dx}_{a}f(x) \cdot dx
&=&
F(a+dx)-F(x)\\
&=&
\underbrace{f(a)}_{\textrm{高さ}} \cdot \underbrace{dx}_{\textrm{底辺}}
\end{eqnarray}\]
3.2. 微分は高さを求める割り算(面積÷底辺)
次に、\(F(x)\) の微分(=接線の傾き)を見てみましょう。
微分(接線の傾き)は「縦÷横」であり、\(F^{\prime}(x)=\) \(\frac{F(a+dx)-F(a)}{dx}\) で求められます。そして、下図で確認できる通り、\(F(a+dx)-F(a)\) は緑の長方形の面積でもあるため、この計算は「面積÷底辺」と同じものであることがわかります。
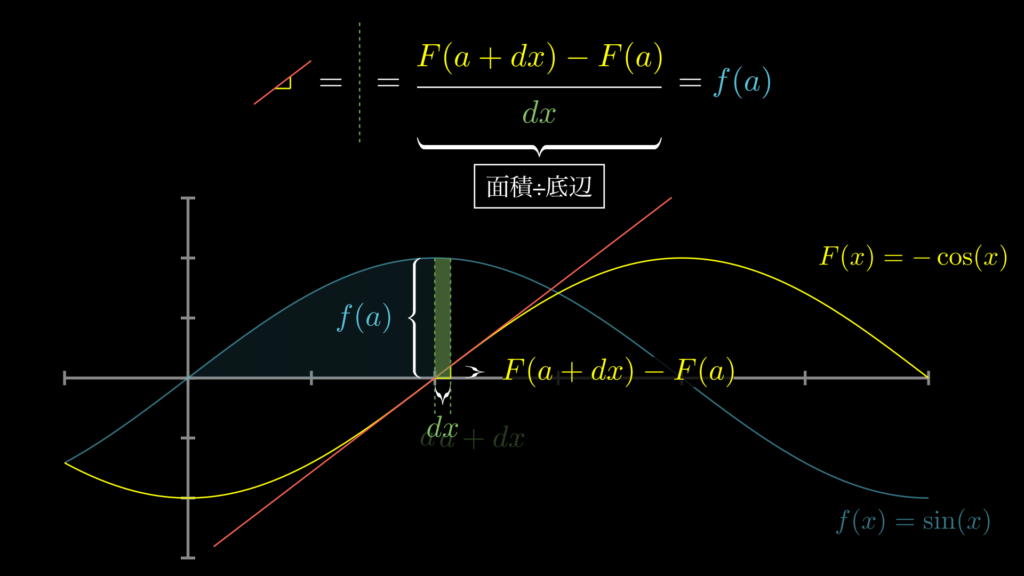
このように、\(F(x)\) の微分である \(f(x)=\frac{F(a+dx)-F(a)}{dx}\) は、実質的には「面積÷底辺」の計算を意味するのです。
\(\underset{dx \rightarrow 0}{\lim}\) のときの [\(a, \ a+dx\)] 区間における長方形の高さ
\[\begin{eqnarray}
F^{\prime}(x)
&=&
\overbrace{\frac{F(a+dx)-F(a)}{\underbrace{dx}_{\textrm{底辺}}}}^{\textrm{面積}}\\
&=&
\underbrace{f(x)}_{\textrm{高さ}}
\end{eqnarray}\]
3.3. “積分vs.微分”は“掛け算vs.割り算”の関係
ポイントをまとめましょう。
ここまで見てきた通り、\(f(x)\) にとって積分 \(F(x)\) は「高さ×底辺」の掛け算であり、長方形の面積を求めることを意味します。そして、\(F(x)\) にとって微分 \(f(x)\) は、「面積÷底辺」の割り算であり、長方形の高さを求めることを意味します。
これは下図を見ていただくと、よりイメージしやすいと思います。
定理より、長方形の面積は \(F(a+dx)-F(a)\) であり、これは \(f(a)\cdot dx\) と等しくなります。そして微分は、この面積を \(dx\) で割ったものなので、\(f(a)\) と等しくなります。

このように積分は長方形の面積を求める掛け算であり、微分は同じ長方形の高さを求める割り算であるため、両者は正反対の処理であるのです。
これを数式で表したものが以下です。
積分と微分は正反対
\[\begin{eqnarray}
\int^{x+dx}_{x}f(x)dx=F(x+dx)-F(x)
\hspace{5mm}
\overset{\textrm{高さ}}{\underset{\textrm{面積}}{\rightleftarrows}}
\hspace{5mm}
f(x)=\frac{F(x+dx)-F(x)}{dx}
\end{eqnarray}\]
以上が、積分が微分の正反対であることの理由です。
4. 積分とは?まとめ
いかがだったでしょうか。以上が積分です。
あらためてまとめると、積分とは、「面積」であり「微分とは反対の演算」です。
例えば、ある関数 \(f(x)\) があるとき、任意の [\(a,b\)] 間の面積はインテグラル記号を使って \(\int^b_a f(x)dx\) と表します。そして、この面積の値は \(F(b)-F(a)\) で求めることができます。これを「微分積分学の基本定理」と言います。
なお、\(F(x)\) は、微分をすると\(f(x)\) になる関数のことで「不定積分」と言います。一方で、\(\int^b_a f(x)dx\) は「定積分」と言います。
それでは、なぜ、積分は微分と正反対と言えるのでしょうか。この点について直感的に理解するための一つの方法は、\(F(x)\) を、上端を変数 \(T\) 、下端を変数 \(0\) とした \(\int^T_0 f(x)dx\) として捉えるというものです。
もう一つの方法は(本質的にはどちらも同じことを言っているのですが…)、積分を長方形の面積を求めるための掛け算と捉え、微分を長方形の面積から高さを求めるための割り算と捉えるというものです。
もしかしたら、これらについては一回読んだだけでは中々しっくりこないかもしれません。その場合は、ぜひ、何度でも読み返すようにしてください。その際は、自分自身で、\(f(x)\) と \(F(x)\) 、そして面積を描いて、イメージしながら読むようにすると必ず理解できるようになります。
以上、当ページが良い学びとなったなら嬉しく思います。




コメント
コメント一覧 (1件)
2.1.速度計だけを見て移動距離を求める
ここで、速度 が なぜ 放物線 を 描くのですか。