sin の積分は -cos になります。それでは、なぜそうなるのでしょうか?ここでは、この理由について誰でも深く理解できるように詳しく解説していきます。読み進めていただくと、なぜ積分は微分の反対なのか、という点も直感的に理解できるようになりますので、ぜひご覧ください。
1. \(\sin(x)\) の積分は \(-\cos(x)\)
定義上、積分は微分と正反対の演算です。そのため、微分をしたら \(\sin(x)\) になる関数が、\(\sin(x)\) の積分です。そして冒頭でお伝えした通り、それは \(-\cos(x)\) です。
\(\sin(x)\) の不定積分は \(-\cos(x)\)
\[\begin{eqnarray}
f(x)=\sin(x)
\hspace{5mm}
\overset{\textrm{積分}}{\underset{\textrm{微分}}{\rightleftarrows}}
\hspace{5mm}
F(x)=-\cos(x)
\end{eqnarray}\]
言ってみれば、これだけなのですが、ここでは「なぜこうなるのか?」についてさらに考えることで、「なぜ積分は微分の反対なのか?」ということを、より深く理解することを目標にして、引き続き解説を進めたいと思います。
2. なぜ \(\sin(x)\) の積分は \(-\cos(x)\) になるのか
積分は微分の反対であることの解説として、「積分とは何か」では、「関数 \(f(x)\) にとっての積分 \(F(x)\)とは、面積を求めるための掛け算であり、関数 \(F(x)\) にとっての微分 \(f(x)\) とは、高さを求めるための割り算である」と理解すれば良いことをお伝えしました。
積分と微分は正反対
\[\begin{eqnarray}
f(x)dx=F(x+dx)-F(x)
\hspace{5mm}
\overset{\textrm{微分(高さ)}}{\underset{\textrm{積分(面積)}}{\rightleftarrows}}
\hspace{5mm}
f(x)=\frac{F(x+dx)-F(x)}{dx}
\end{eqnarray}\]
ここでは、これとはまた異なるアプローチで、積分は微分の反対であること(\(\sin\) の積分は \(-\cos\) であること)を詳しく解説していきます。
具体的には、まず関数 \(f(x)=\sin(x)\) の平均値を求める方法を考え、次に \(f(x)\) の平均値と \(F(x)\) の関係について考えることで、積分は微分の反対であることが直感的にわかるようになります。
それでは早速、始めましょう。
2.1. 関数の平均値を求める
「関数 \(f(x)\) の平均値を求める」という問題は、積分を学ぶときに必ず扱うことになるものです。これは、さまざまな点でとても重要です。
例えば、季節ごとの日照時間のサイクルの算出には \(\sin\) を使った \( ” 2.7\sin(2\pi x/365)+12.4 ” \) というような関数が用いられます。そして、この関数の平均値を算出すると、一年間の平均日照時間が分かります。それによって太陽電池の発電効率や作物の日照時間などを最適化することができるのです。
そして、関数の平均値について深く考えることは、積分と微分がお互いに正反対の関係にあるということを、より深く理解するためにも非常に役に立ちます。
そこで、ここでは \(\sin(x)\) の平均値について考えていくことにしましょう。
2.1.1. 平均値の算出方法は積分とほぼ同じ
いきなりですが、\(\sin(x)\) の [\(0, \pi\)] 区間における平均値(=平均の高さ)はどうなるでしょうか。少し考えてみてください。
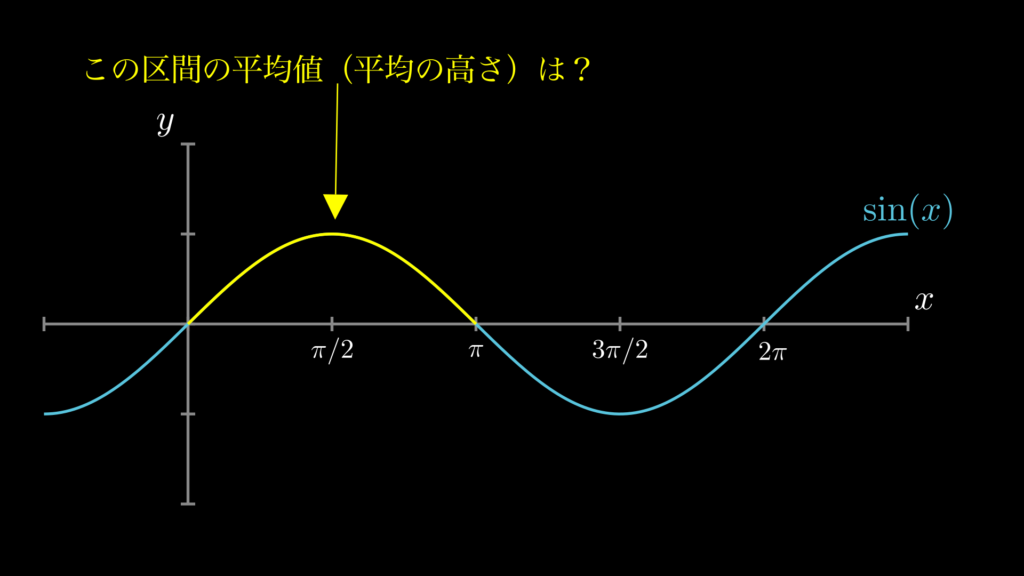
通常であれば、平均値は「値の合計÷値の個数」で求められます。例えば、4つの値 \(2,4,6,8\) があるとき、これらの値の平均値は \(\frac{2+4+6+8}{4}=5\) になります。つまり平均値とは、原則として離散値の概念なのです。しかし \(\sin(x)\) は離散値ではなく連続値であり、[\(0, \pi\)] 区間には、\(\sin(x)\) の値が無限に存在します。そのため、そのままでは平均値を計算することができません。
数学では、このようなケースは多々あります。そして、このようなときは \(0\) から \(\pi\) の間で、間隔を \(dx\) とした有限個の点を抽出して平均を算出するという方法を取ります。
例として以下の画像をご覧ください。これは等間隔の10個の点を選び、それらの地点での \(f(x)\) の値を算出することで、平均値を求めているものです。
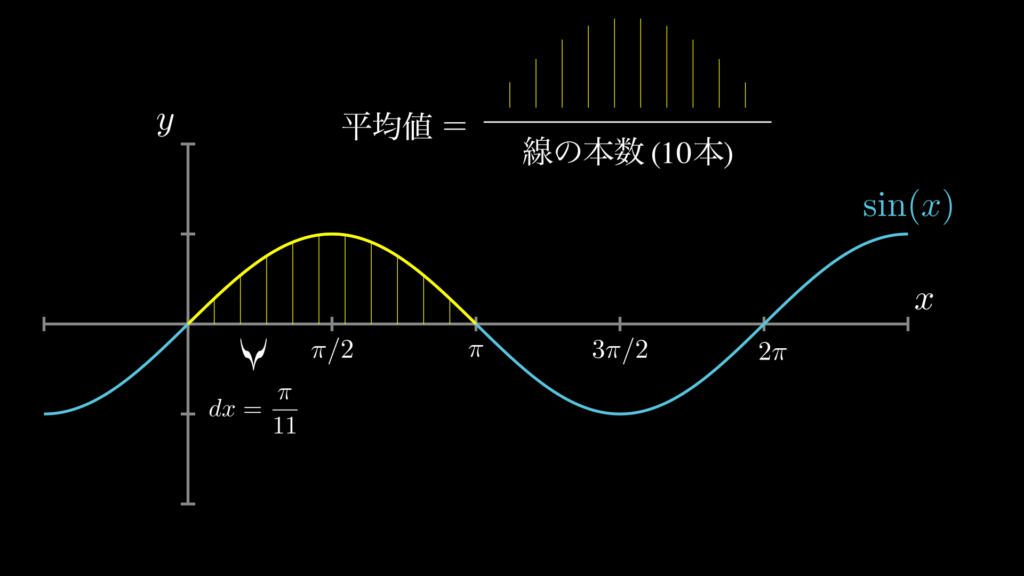
計算式
\[\begin{eqnarray}
\text{平均値}
&=&
\dfrac{\sum_{k=1}^{10} \sin(\frac{k\pi}{11})}{10}\\
&=&
\dfrac{\sin(\frac{\pi}{11})+\sin(\frac{2\pi}{11})+ \cdots + \sin(\frac{10\pi}{11})}{10}\\
&\approx&
0.695515 \cdots
\end{eqnarray}\]
※線の数が10本なので、\(dx=\frac{\pi}{10+1}\) 。\(dx\) は線の間隔のこと。
このようにすると、おおよその平均値を求めることができます。しかし、線が10本だけでは、まだ実際の平均値とは大きな隔たりがありそうです。そこで、次は線の数を100本にしてみましょう。
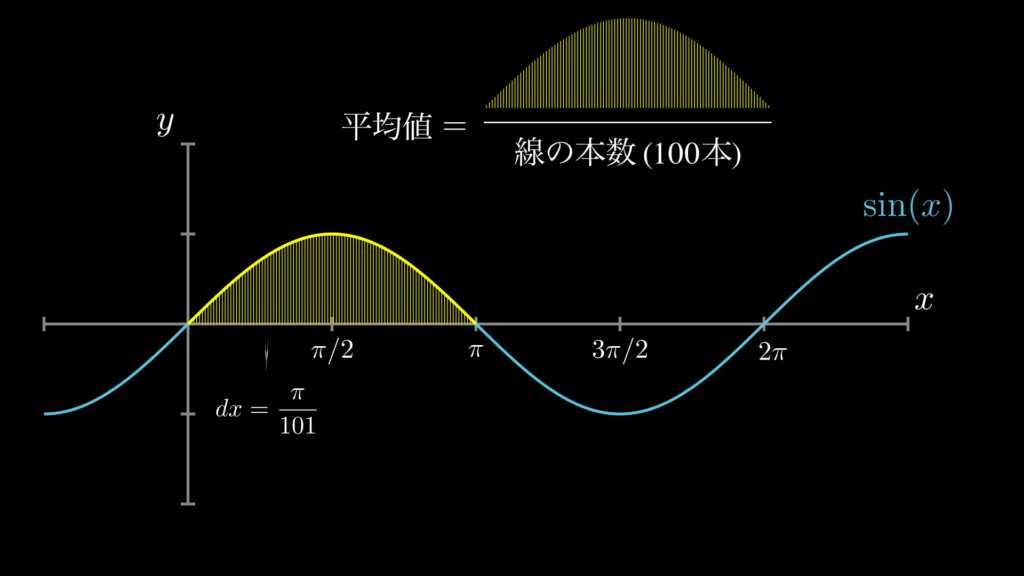
計算式
\[\begin{eqnarray}
\text{平均値}
&=&
\dfrac{\sum_{k=1}^{100} \sin(\frac{k\pi}{101})}{10}\\
&=&
\dfrac{\sin(\frac{\pi}{101})+\sin(\frac{2\pi}{101})+ \cdots + \sin(\frac{100\pi}{101})}{100}\\
&\approx&
0.642934 \cdots
\end{eqnarray}\]
※線の数が100本なので、\(dx=\frac{\pi}{100+1}\) 。\(dx\) は線の間隔。
こうして線の数を1000本、10000本増やしていくと(=\(dx\) を狭めていくと)、平均値はどんどん「ある値」に収束していきます。そして、この収束値こそが、関数 \(\sin(x)\) の [\(0,\pi\)] 区間における平均値であるということになります。
さて、もうお気づきでしょう。このプロセスは積分と同じです。そのため積分式 \(“\int^{\pi}_{0}\sin(x)dx”\)を変換することで、平均値算出式を求めることができそうです。
2.1.2. 積分式から平均値の公式を求める
おさらいですが、積分は、任意の [\(a,b\)] 区間における無数の長方形の面積 \(“\sin(x) dx”\) の合計 \(“\int^b_a \sin(x)dx”\)です。これに対して、平均値は任意の [\(a,b\)] 区間における無数の線の高さ \(“\sin(x)”\) の合計 \(“\int^b_a \sin(x)”\) を線の本数で割ったものです。
面積と平均値
\[\begin{eqnarray}
\mathrm{面積}=\int^{\pi}_0 \sin(x)dx
\hspace{5mm}
\Longleftrightarrow
\hspace{5mm}
\mathrm{平均値}=\frac{\int^{\pi}_0 \sin(x)}{\mathrm{線の本数}}
\end{eqnarray}\]
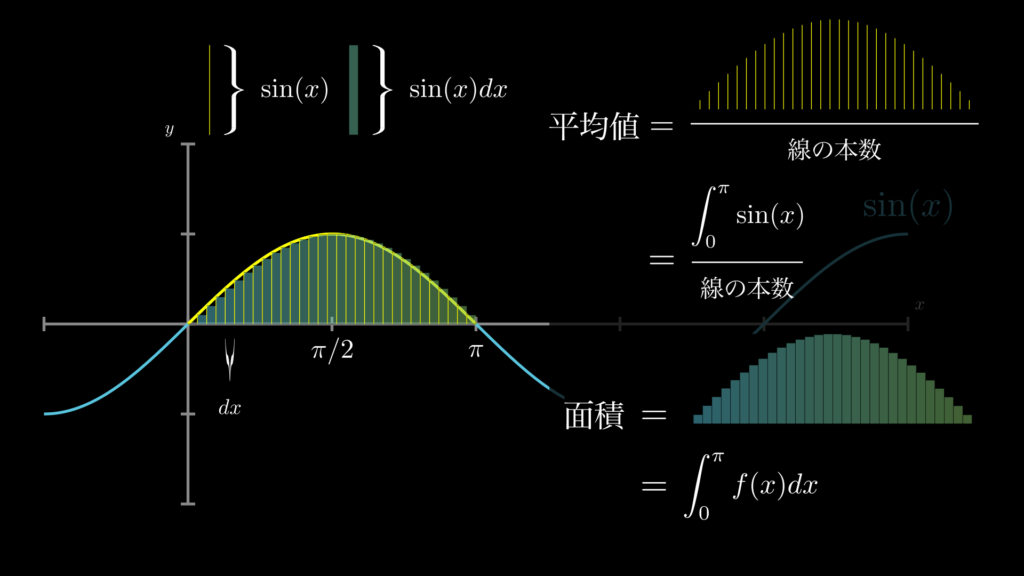
さて、平均値を求める際の分母である「線の本数」は、線の間隔 \(dx\) によって異なります。例えば、[\(0,\pi\)] の間で \(dx=1\) なら線の本数は \(\pi ÷ 1=3\)本になりますし、\(dx=0.3\) なら線の本数は \(\pi ÷ 0.3=10\)本になります。
なお \(\pi\) は \(3.141592\cdots\) という無理数のため、割り切ることはできませんが、四捨五入して考えて全く問題ありません。\(dx\) は実際には、限りなく \(0\) に近い値であるため、少々の誤差は関係なくなってしまうからです。
以上のことから、平均値を求める際の分母である「線の本数」は \(\dfrac{\pi-0}{dx}\) で求められることがわかります。そのため平均値の式は、以下のように書き換えることができます。
\[\begin{eqnarray}
\mathrm{平均値}
&=&
\frac{\int^{\pi}_0 \sin(x)}{\mathrm{線の本数}}\\
&=&
\frac{\int^{\pi}_0 \sin(x)}{\frac{\pi-0}{dx}}\\
&=&
\frac{\int^{\pi}_0 \sin(x)dx}{\pi}
\end{eqnarray}\]
ここで、分子の \(\int^{\pi}_0 \sin(x)dx\) にご注目ください。これは、積分(面積)と同じものになっています。
つまり、平均値(高さの平均)は「面積(積分)÷ 横幅(範囲)」で求めることができるということです。もともと面積は「高さ×横幅」なので、これは直感的にもすんなりと理解できるでしょう。
というわけで、これを一般化すると、以下の通り、平均値を求めるための公式が求められます。
関数の平均値の公式
\[\begin{eqnarray}
\mathrm{平均値}
&=&
\frac{\int^{b}_a f(x)dx}{b-a}\\
&=&
\frac{F(b)-F(a)}{b-a}
\end{eqnarray}\]
2.1.3. 実際に平均値を求めてみよう
それでは実際に平均値を求めてみましょう。
まず、\(\sin(x)\) の不定積分は \(-\cos(x)\) です。このことから、「微分積分学の基本定理」 \(“\int^b_a f(x)dx=F(b)-F(a)”\) より、\(\int^{\pi}_{0} \sin(x)dx=2\) であることが求められます。
微積分の基本定理で面積を求める
\[\begin{eqnarray}
\mathrm{面積}=
\int^{b}_a f(x)dx
&=&
F(b)-F(a)\\
\longrightarrow
\int^{\pi}_0 \sin(x)dx
&=&
(-\cos(\pi))-(-\cos(0))\\
&=&
(1)-(-1)\\
&=&
2\\
\end{eqnarray}\]
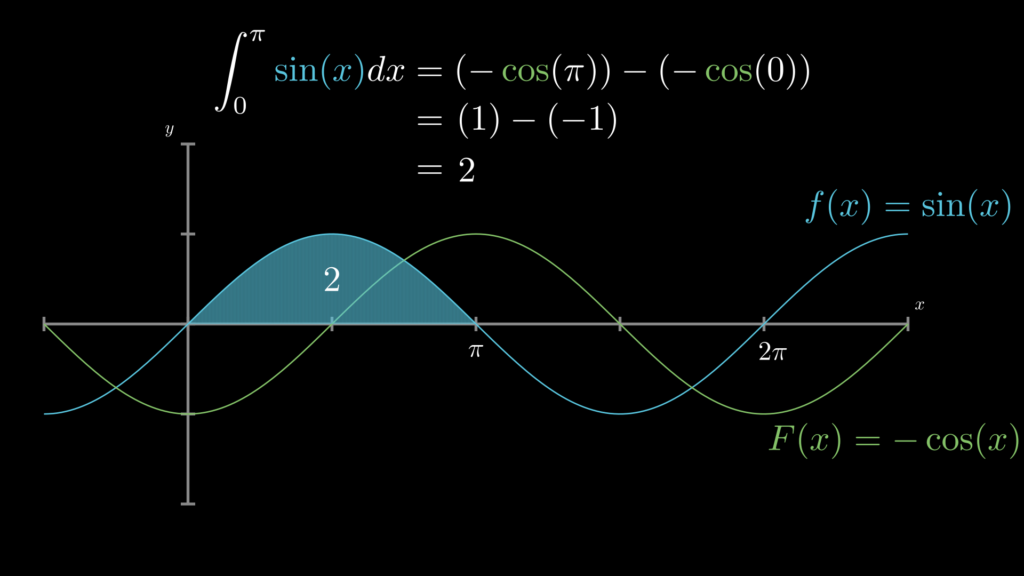
この面積を範囲で割ったものが、[\(0,\pi\)] 区間における \(\sin(x)\) の平均値です。
平均値
\[\begin{eqnarray}
\mathrm{平均値}
&=&
\frac{\int^{\pi}_0 \sin(x)dx}{\pi-0}\\
&=&
\frac{2}{\pi}\\
&=&
0.642934 \cdots
\end{eqnarray}\]
以上が、任意の関数の指定の範囲における平均値の求め方です。
先ほど、この平均値の求め方を知ることが、積分と微分が正反対であることを理解するための助けとなる、と述べました。それはなぜでしょうか。次から、この点について考えていきましょう。
2.2. 関数の平均値と積分の関係
さて、ここまでは関数の平均値を求めるにはどうしたら良いかということを考えてきました。そして、それに先立って、積分と微分が正反対であることを直感的に理解するための助けになるということをお伝えしていました。
これはどういうことなのでしょうか。
結論から言うと、「\(f(x)\) の平均値が『面積(積分)÷範囲』で求められる」ということは、つまり、「関数 \(f(x)\) の平均値と関数 \(F(x)\) の傾きは同じである」ということを意味します。
このことから、積分と微分はお互いに正反対の演算であるという事実が鮮明になります。
詳しく見ていきましょう。
2.2.1. \(f(x)\) の平均値は \(F(x)\) の傾きと同じ
[\(a, b\)] 間の \(f(x)\) の平均値を求めるということは、この区間の面積(積分)である \(F(b)-F(a)\) を、その範囲 \(b-a\) で割るということでした。 そして、この \(f(x)\) の平均値は、不定積分 \(F(x)\) の視点から見ると、その区間における関数の傾きと等しいのです。参考に以下の画像をご確認ください。
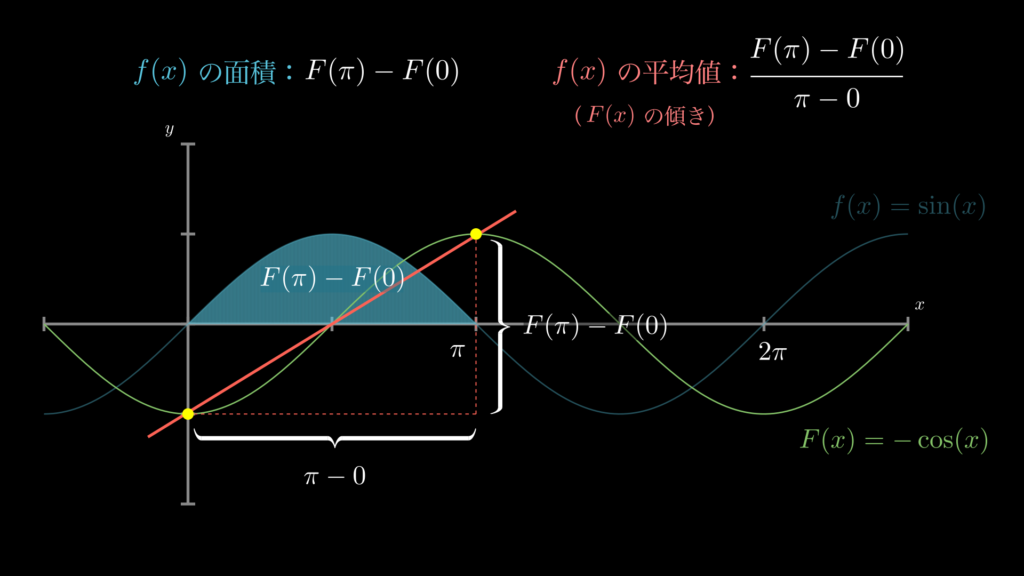
こうして視覚的に確認してみると、次の点がわかりやすくなります。
- 関数 \(f(x)\) の [\(0,\pi\)] 区間の面積は \(F(\pi)-F(0)\)
- \(F(\pi)-F(0)\) は関数 \(F(x)\) の高さの変化と等しい
- 関数 \(f(x)\) の平均値 \(\frac{F(\pi)-F(0)}{\pi-0}\) は関数 \(F(x)\) の[\(0,\pi\)] 区間の傾きと等しい
繰り返しになりますが、任意の区間における \(f(x)\) の平均値と \(F(x)\) の傾きは等しいのです。ここまで来たら、\(F(x)\) の微分が \(f(x)\) であるということは、もうわかるでしょう。
2.2.2. \(F(x)\) の微分は \(f(x)\) になる
ここまでは [\(0,\pi\)] 区間について見てきました。次に、この範囲をグッと縮めて [\(a, a+dx\)] 区間で見てみましょう。そうすると、以下の画像で示しているように、\(f(x)\) の平均値(\(= f(x)\) の値)の計算式は、そのまま \(F(x)\) の微分の式になっていることがわかります。
なお、[\(a, a+dx\)] 区間において、「\(f(x)\) の平均値 \(= f(x)\) の値」と考えてよくなる理由は、\(dx\) は限りなく \(0\) に近い値だからです、例えば、\(\frac{f(1)+f(1.00 \cdots 01)}{2}\) は \(f(1)\) であると言えますね。
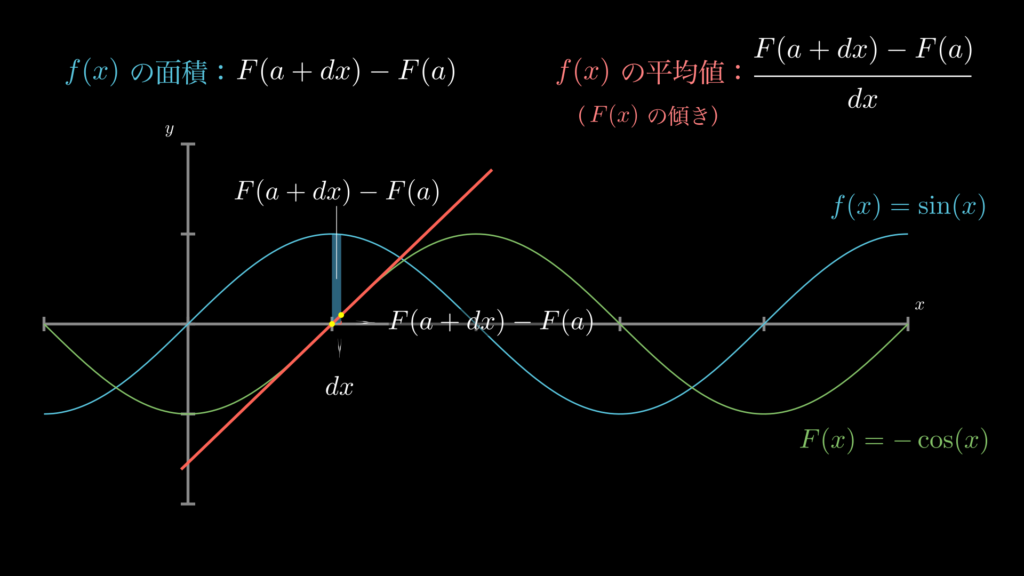
以上のことから、\(F^{\prime}(x)=\frac{F(a+dx)-F(a)}{dx}=f(x)\) であることがわかります。つまり、\(F(x)\) の微分は \(f(x)\) になるということです。
こうしたことから、\(\sin(x)\) の積分は \(-\cos(x)\) になるのですね。
\[\begin{eqnarray}
-\cos^{\prime}(x)
&=&
\frac{\{-\cos(a+dx)\}-\{-\cos(a)\}}{dx}\\
&=&
\sin(x)
\end{eqnarray}\]
3. \(\sin\) の積分のまとめ
以上が \(\sin(x)\) の積分が \(-\cos(x)\) であることの理由です。
文中で解説したように、ある関数 \(f(x)\) の平均値を求めることは、とても重要な計算です。そして、この重要な計算について深く考えていくと、積分が微分の反対であることが深く理解できるようになっています。
これについて、ぜひ腑に落ちるまで何度でも読み直すようにしてください。




コメント