ひろ– Author –
-

マルコフ連鎖モンテカルロ法を誰でも理解できるようにわかりやすく解説
マルコフ連鎖モンテカルロ法(MCMC)は、ベイズ推定において、事後分布を求めるのが計算上余りにも困難な場合に、事前分布と尤度分布を材料として乱数を無作為抽出することで、事後分布を概算する方法のことです。 そうは言っても、これだけでは全く意味が... -

確率分布を誰でも理解できるようにわかりやすく解説
確率分布は、簡潔に言うと「ある試行で起こり得るすべての事象の確率を出力する関数」です。現実世界の実に様々な現象を、確率分布一つで表すことができるため、特に統計学の世界で非常に重宝されています。 このページでは、この確率分布についてわかりや... -

一様分布を誰でも理解できるようにわかりやすく解説
一様分布は、離散型でもあり連続型でもある確率分布です。ある試行のすべての事象の確率が均一である場合の分布であり、非常に単純なものですが、ベイズ統計において事前情報が何もない場合の事前分布として使われるという点で有用です。 当ページでは、こ... -

ベルヌーイ分布を誰でも理解できるようにわかりやすく解説
ベルヌーイ分布は確率分布の中でもっともシンプルであるため、最初に学ぶのに最適なものです。当ページでは、このベルヌーイ分布について知っておきたい、以下の 6 つの点を解説します。 ベルヌーイ分布とは何かベルヌーイ分布の確率関数ベルヌーイ分布の... -

共役事前分布とは?誰でも理解できるようにわかりやすく解説
共役事前分布とは、連続型確率分布を使ったベイズ推定の計算を簡単にしてくれるものです。 『ベイズ推定とは?誰でも理解できるようにわかりやすく解説』では、離散型確率分布を例にベイズ推定の計算を行いましたが、これの連続値バージョンとお考え頂くと... -

ガンマ分布とは?誰でも理解できるようにわかりやすく解説
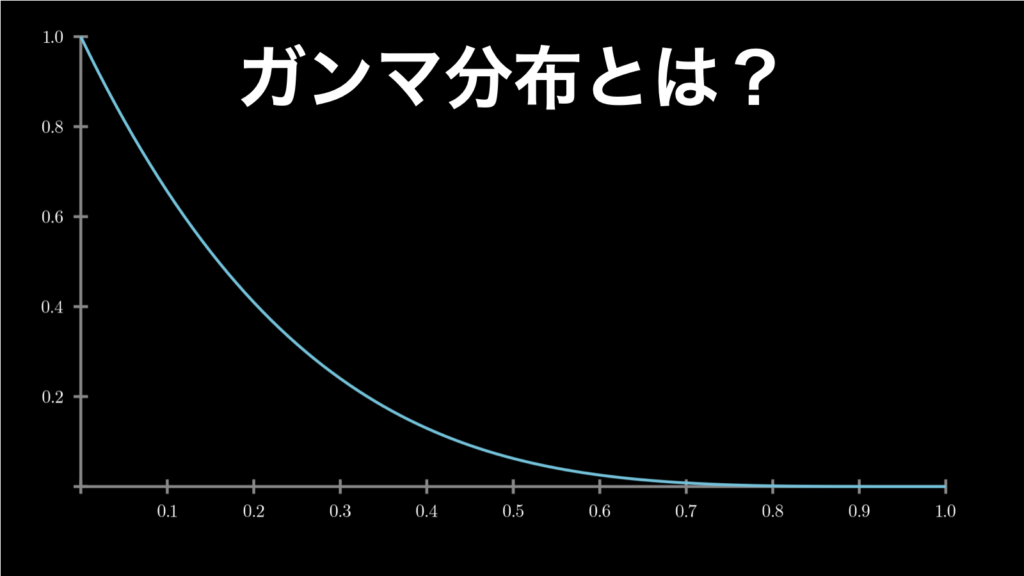
ガンマ分布は、「任意の単位時間や単位面積 λ の間に 1 回起きることが期待できる出来事が、実際に起きるまでの時間の分布」です。主に信頼性工学や通信工学において使われますが、以下のような実用例があります。 体重の分布エイズの潜伏期間システム・ダ... -

ポアソン分布とは?誰でも理解できるようにわかりやすく解説
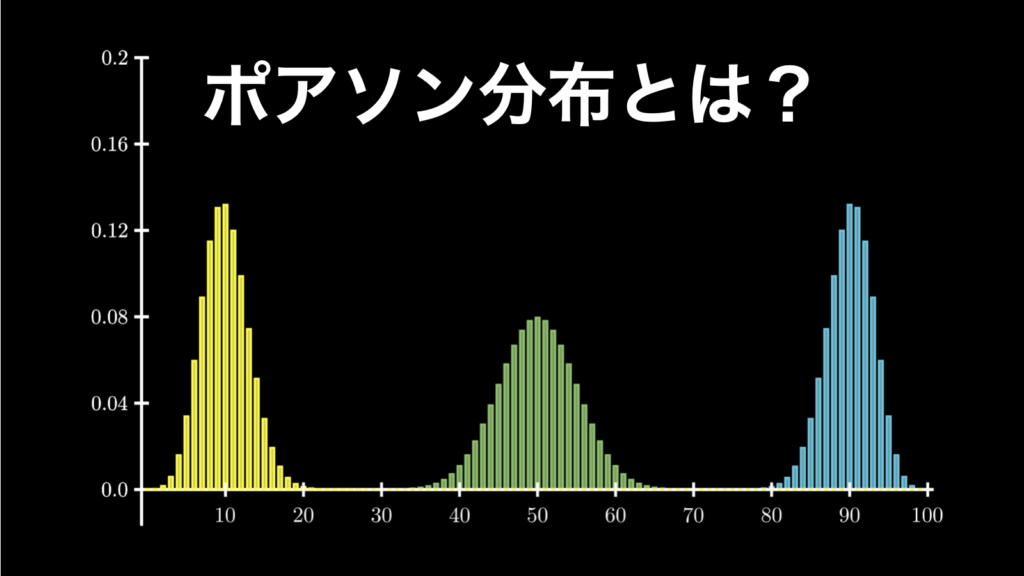
ポアソン分布は、統計学において使われる代表的な離散確率分布の一つであり、「稀にしか起こらないような現象が、一定の期間内に何回起こることが期待できるかの確率の分布」です。ベイズ統計において、同じ離散確率分布の二項分布と並んで扱う機会が多い... -

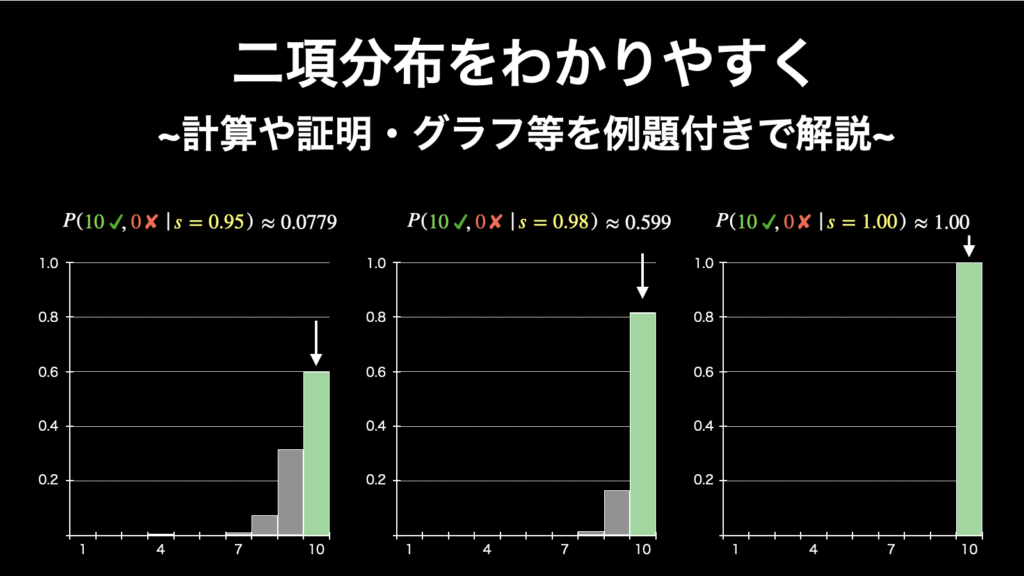
二項分布を誰でも理解できるようにわかりやすく解説
二項分布は離散確率分布の代表的なものの一つで、「試行回数 n と成功率 p が明らかなときの、成功回数 k の分布」のことです。試行回数と成功率という二つのパラメータさえあれば良いので、使う機会が非常に多い確率分布です。 その使用頻度の多さから、... -

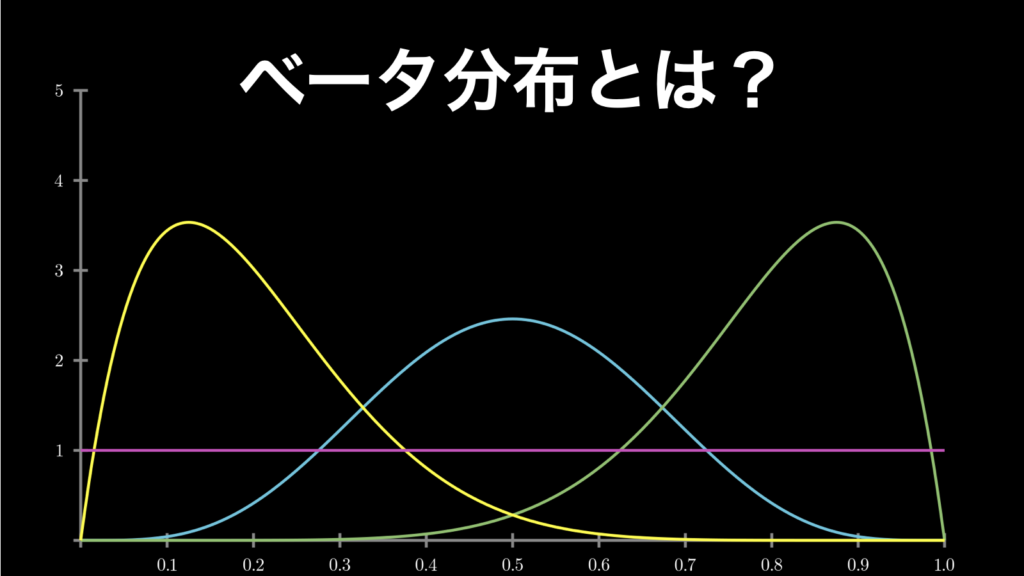
ベータ分布とは?誰でも理解できるようにわかりやすく解説
ベータ分布は、「成功数 α と失敗数 β が明らかなときの成功率」の連続値型確率分布です。当ページでは、このベータ分布について詳しく解説していきます。具体的には、以下の内容を知ることができます。 それでは早速見ていきましょう。 なお、まだ『確率... -

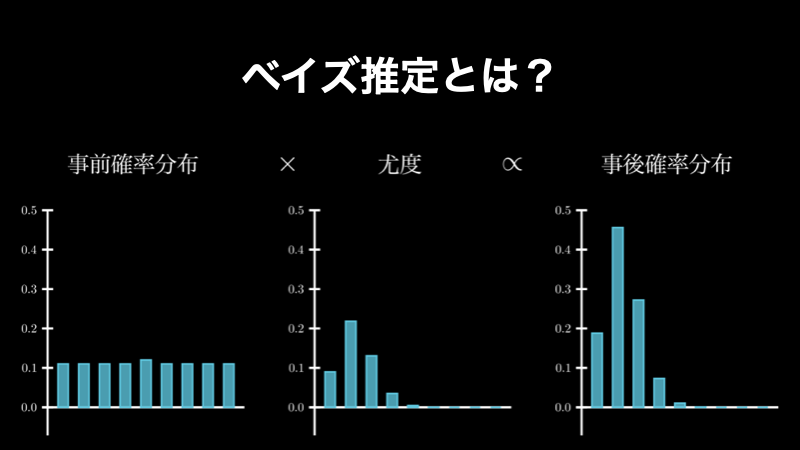
ベイズ推定とは?誰でも理解できるようにわかりやすく解説
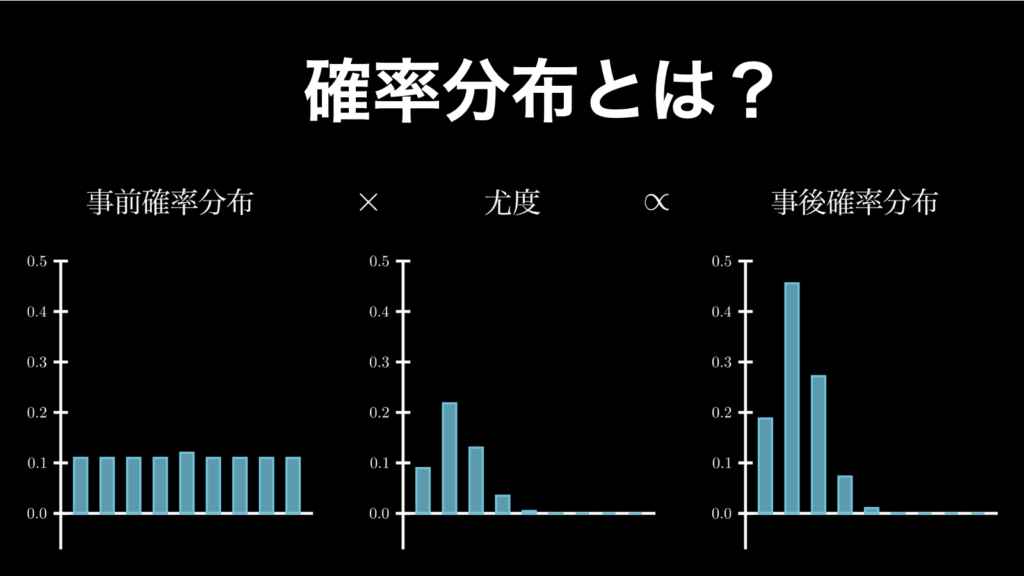
ベイズ推定は、ベイズの定理を使った統計的推定方法の一つです。具体的にはベイズの定理の確率を、確率分布に置き換えたものであり、「事前確率分布と尤度関数から、事後確率分布を求める」というものです。ちょうど、下図のようなイメージです。 そして、... -

ベイズの定理 とは?誰でも理解できるようにわかりやすく解説
ベイズの定理は、簡潔に述べると「事前確率(もともと持っている信念や考え)が尤度(新しいデータや経験)を受けて、どう変化するのかを示す事後確率を求めるための方法」です。 ベイズの定理は今では、統計学の主流であり、人工知能やディープ・ラーニン... -

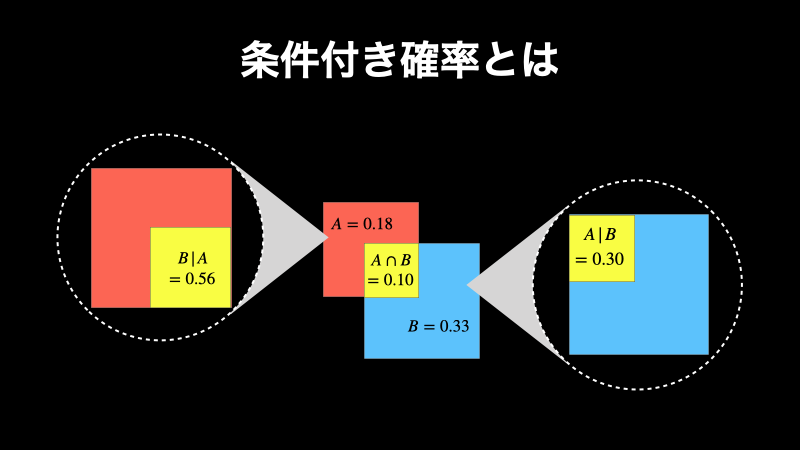
条件付き確率とは?誰でも理解できるようにわかりやすく解説
条件付き確率とは、「事象 B が起こった条件下での事象 A の確率」のことです。このページでは、この条件付き確率についてわかりやすく解説していきます。具体的には以下の内容を知ることができます。 条件付き確率とは何かが具体的にわかる条件付き確率の...