ベルヌーイ分布を誰でも理解できるようにわかりやすく解説

2021 11/01

2021年11月1日 2021年11月1日

ベルヌーイ分布は確率分布の中でもっともシンプルであるため、最初に学ぶのに最適なものです。当ページでは、このベルヌーイ分布について知っておきたい、以下の 6 つの点を解説します。

ベルヌーイ分布とは何か
ベルヌーイ分布の確率関数
ベルヌーイ分布の期待値
ベルヌーイ分布の分散
ベルヌーイ分布のグラフ
二項分布との違い

ぜひ参考にして頂ければと思います。

1. ベルヌーイ分布とは

ベルヌーイ分布は、結果が 2 つで、確率が一定で、お互いに独立の試行（「ベルヌーイ試行」という）の確率を表す確率分布です。

ベルヌーイ試行の代表例はコイントスでしょう。コイントスを行うと起こり得る事象は、「表が出る」「裏が出る」の 2 つだけです。表が出るという事象を \(x=1\)、裏が出るという事象を \(x=0\) にして、コイントスの確率分布のグラフを描くと、下図のようになります。

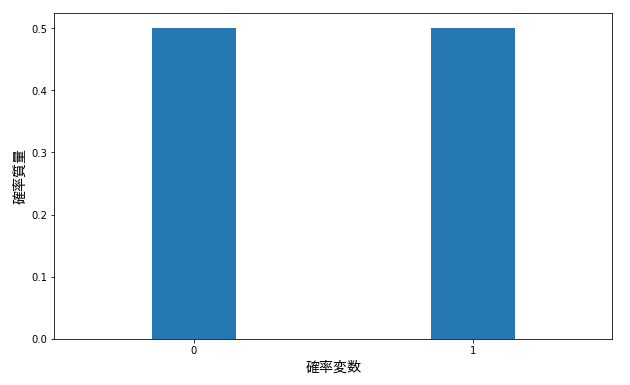
このことからコイントスでは、表が出る確率も裏が出る確率も同じ \(0.5\) であることがわかります。このように、あるベルヌーイ試行において、事象 \(x=0\) が起こる確率、事象 \(x=1\) が起こる確率を明らかにしてくれるのがベルヌーイ分布です。

ベルヌーイ分布（コイントスで表が出る確率と裏が出る確率）

\[\begin{eqnarray}
\overset{\small 入力値(確率変数)}
{\begin{matrix}
x=1 \ \ ({\small 表})\\
x=0 \ \ ({\small 裏})
\end{matrix}}
\rightarrow \ \
\underset{\small ベルヌーイ分布(確率関数}{p(X=x)}
\ \rightarrow \
\overset{\small 出力値(確率)}
{\begin{matrix}
0.5 \ \ ({\small 表の確率})\\
0.5 \ \ ({\small 裏の確率})
\end{matrix}}
\end{eqnarray}\]

これが何の役に立つのでしょうか？

コイントスでは、イカサマコインでなければ表が出る確率も裏が出る確率も \(0.5\) であることは、ベルヌーイ分布を使わずとも分かりきっています。

しかし、現実世界では、このような確率（成功率 \(x\)・失敗率 \(1-x\)）は分かっていないことの方が遥かに多いです。そのような場合に、観察から、もっともあり得る成功率・失敗率を明らかにしてくれるのがベルヌーイ分布です。

たとえば、ある病気の新薬ができたとします。これを患者に投与して、治癒したという事象 \((x=1)\)、治癒しなかったという事象 \((x=0)\) を観察した場合の治癒率を検証する、といった場合に、このベルヌーイ分布が活用されています。

2. ベルヌーイ分布の確率質量関数

ベルヌーイ分布の確率質量関数は以下の通りです。

ベルヌーイ分布の確率質量関数

\[\begin{eqnarray}
f(k)=
\begin{cases}
1-p, \ \ \ &k= 0 {\small \ のとき}& \\
p, &k= 1 {\small \ のとき}&
\end{cases}
\end{eqnarray}\]

または次の式で表されることも多いです。

\[\begin{eqnarray}
f(k|p)=p^k(1-p)^{1-k}
\end{eqnarray}\]

これは単純に、確率変数 \(1\) の事象が起こる確率は \(p\) になり、確率変数 \(0\) が起こる確率は \(1-p\) になりますよ、と言っているだけであり、それ以上の意味はありません。

3. ベルヌーイ分布の期待値

ベルヌーイ分布の期待値は以下の通りです。

ベルヌーイ分布の期待値

\[\begin{eqnarray}
{\rm E}[X]=\sum kP(X=k)=p
\end{eqnarray}\]

要するに、ベルヌーイ分布の期待値（平均値）は、事象 \(x=1\) が起きる確率と同じであるということです。

4. ベルヌーイ分布の分散

ベルヌーイ分布の分散は以下の通りです。

ベルヌーイ分布の分散

\[\begin{eqnarray}
{\rm V}[X]
=
{\rm E}[(X-{\rm E}[X])^2]
=
p(1-p)
\end{eqnarray}\]

ただしベルヌーイ分布では、確率変数の実現値は \(0\) と \(1\) の 2 つだけなので、分散を使うようなケースはありません。

5. ベルヌーイ分布のグラフ

上でも見ましたが、離散確率分布であるベルヌーイ分布のグラフは、2 本の棒のみの棒グラフになります。

もう一つ例を貼っておきましょう。下図は \(p=0.7\), \({\rm E}[X]=0.7\), \({\rm V}[X]=0.21\) のベルヌーイ分布のグラフです。

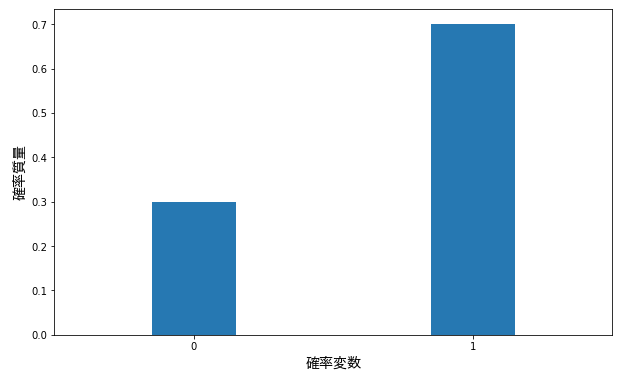
6. ベルヌーイ分布と二項分布の違い

ベルヌーイ分布は、ベルヌーイ試行を何度も行ったときの成功率の確率分布です。一方で、二項分布はベルヌーイ試行を何度も行ったときの成功回数の確率分布です。

両者は似通っており、ベルヌーイ分布を知っていれば、二項分布の理解にも役立ちます。二項分布については『二項分布とは？誰でも理解できるようにわかりやすく解説』で解説しているので、ぜひご覧ください。

まとめ

以上がベルヌーイ分布です。あらためて確認のために基本情報を載せておきます。

ベルヌーイ分布の基本情報

確率関数	\(\begin{eqnarray} f(k)= \begin{cases} 1-p, \ \ \ &k= 0 {\small \ のとき}& \\ p, &k= 1 {\small \ のとき}& \end{cases} \end{eqnarray}\) \(f(k\|p)=p^k(1-p)^{1-k}\)
期待値	\(E(X)=p\)
分散	\(V(X)=p(1-p)\)