二項分布は離散確率分布の代表的なものの一つで、「試行回数 n と成功率 p が明らかなときの、成功回数 k の分布」のことです。試行回数と成功率という二つのパラメータさえあれば良いので、使う機会が非常に多い確率分布です。
その使用頻度の多さから、ベイズ統計においても、ベータ分布と並んで真っ先に学ぶものです。当ページでは、この二項分布について知っておくべきことを、誰でもわかるように解説していきます。具体的には、以下のようなことを身につけることができます。
- 二項分布とは何か?どのような分析が可能になるのか?:まずは、二項分布がどのような確率分布であるのか、主にその確率質量関数について解説します。そして、二項分布の代表的な分析指標である期待値(平均値)と分散の公式について解説します。
- 二項分布と正規分布の関係がわかる:二項分布がある条件を満たすときは、正規分布とほとんど全く同じように使うことができます。そのための条件を解説します。
- 二項分布の例題を解くことで、実践的な活用方法がわかる:最後に、二項分布の代表的な練習問題を 2 つ用意しています。これを解くことで、当ページで学んだ内容を実践で活用するための練習となります。実際に問題を解くことは、理解を定着させるために必須のステップなので、ぜひチャレンジしてください。
なお、ベイズ統計学において、二項分布と対になる存在であるベータ分布については『ベータ分布とは?誰でも必ず理解できるようにわかりやすく解説』で解説していますので、ぜひ合わせてご確認ください。
それでは始めましょう。
1. 二項分布とは
二項分布は、試行回数 \(n\) と成功率 \(p\) という 2 つのパラメータがあるときに成功回数の確率を表す確率分布です。
たとえばバスケットボールのフリースローを考えてみてください。フリースロー成功率が 70% の選手が 10 回フリースローを行ったとしたら、成功数の分布は下図の通りになります。
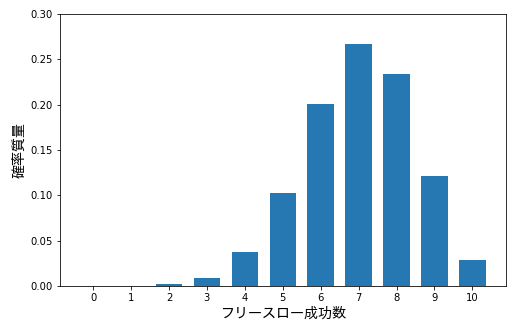
この確率分布を見たら、この選手がフリースローを 10 本全部決める確率は大体 3% ほどで、5 回しか決められない確率は 10% あるなど、成功回数について様々なことがわかります。
二項分布のグラフ
成功率が 0.1 から 0.9 の場合を並べると下図のようになります。
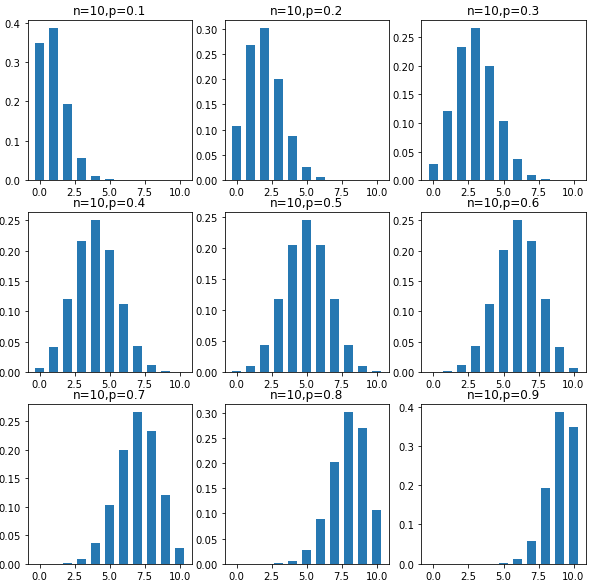
ご覧の通り、\(p < 0.5\) のときは右肩下がりに、\(p = 0.5\) のときは正規分布に近似し、\(p > 0.5\) のときは右肩上がりになります。
以上が二項分布です。これは試行回数 \(n\) と成功率 \(p\) の 2 つのパラメータさえあれば求められる、非常に便利な確率分布です。
2. 二項分布の確率質量関数
二項分布の確率質量関数は以下の通りです。
二項分布の確率質量関数
\[
{\rm Bin}(k|n,p)
=
\dbinom{n}{k} \ p^k(1-p)^{n-k}
\]
※ \(k\) : 成功数(確率変数), \(n\) : 試行回数, \(p\) : 成功率, \(\binom{n}{k}\) : 二項係数 \({}_nC_{k}\) と等しい
\(\binom{n}{k}\) の部分は「二項係数」と言います。これは組み合わせ論の \({}_nC_k\) とまったく同じものです。組み合わせについては、「組み合わせとは?知っておくべき 2 つの公式」で解説していますので、ぜひご確認ください。\(p^k(1-p)^{n-k}\) の部分はベルヌーイ分布と非常に似通っています。
二項分布の確率質量関数の導出
なぜ、この確率質量関数で二項分布を描くことができるのでしょうか。これについては以下のボックス内で解説していますので、興味のある方はご覧ください。
3. 二項分布の期待値(平均)
二項分布の期待値は以下の公式で求められます。
二項分布の期待値
\[\begin{eqnarray}
E(X)=np
\end{eqnarray}\]
※ \(n\) : 試行回数, \(p\) : 成功率
期待値は、その試行を繰り返し何度も行ったときに最終的に収束していく先の値です。例えば、試行回数 \(n =5\) 、成功率 \(p = 0.5\) の試行の期待値は \(np=5 \cdot 0.5 = 2.5\) です。これは、この試行を繰り返し行うと、最終的に \(k = 2.5\) に近づいていくということを意味します。
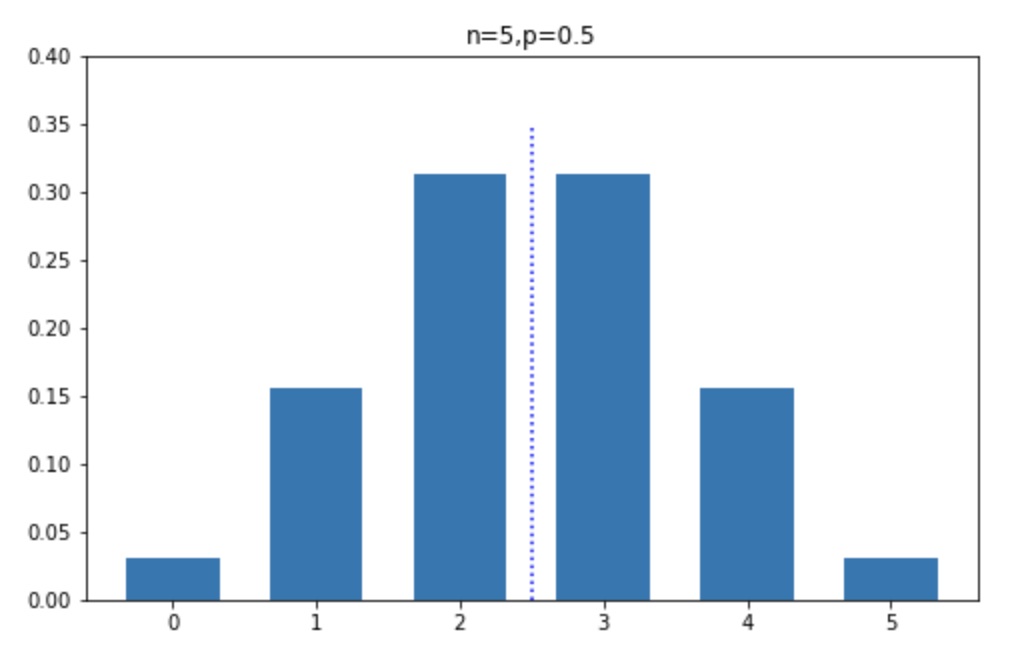
二項分布の期待値の導出
二項分布の期待値の導出方法については、以下のボックス内で示していますので、ご興味のある方はクリックしてご覧ください。
4. 二項分布の分散
二項分布の分散は以下の公式で求められます。
二項分布の分散
\[\rm{Var}(X)=np(1-p)\]
※ \(n\) : 試行回数, \(p\) : 成功率
分散は、分布の横への広がり具合を示します。たとえば \(p = 0.5\) で \(n\) を増やしていくと、下図のように分散は大きくなり、最大値は小さくなっていくことがわかります。
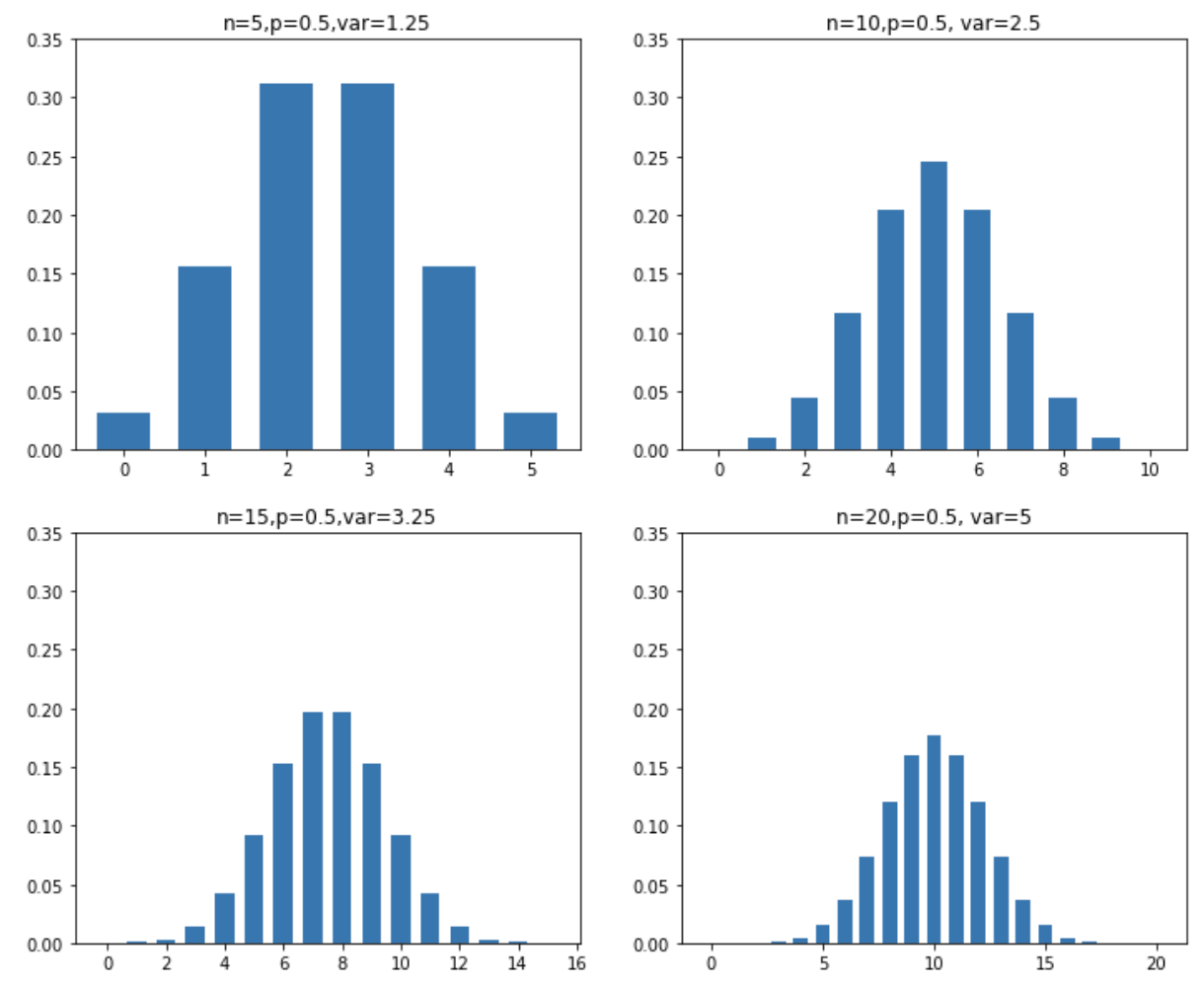
二項分布の分散の導出
二項分布の分散の導出方法については、以下のボックス内で示していますので、ご興味のある方はクリックしてご覧ください。
5. 二項分布と正規分布の近似
期待値と分散を使うと、二項分布と正規分布の関係も理解することができます。その関係とは、二項分布は、期待値 \(np\) と分散 \(np(1-p)\) が \(5\) よりも大きい場合に、正規分布と非常に近似するという点です。
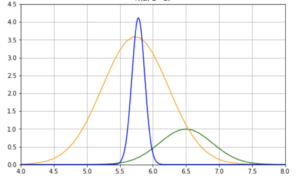
極端な例ですが、条件を満たさない例と満たす例を、下図に示しています。
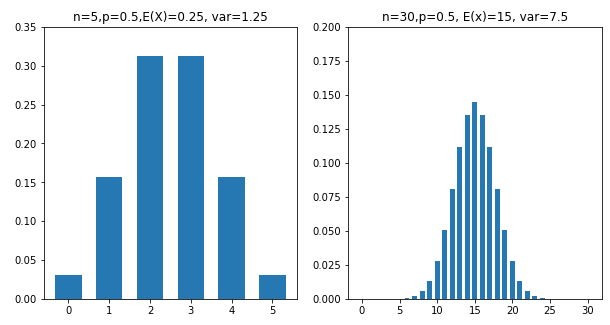
このように、\(n\) が十分に大きく、期待値も分散も十分に大きい場合、二項分布は、正規分布 \(\rm{N}(np. np(1-p))\) に近似することになります。
6. 二項分布の例題
それでは二項分布の使い方に関して理解を深めるために、次の問題に挑戦してみてください。
6.1. 当選率
選挙の当選率は?
あなたは選挙の立候補者 A の右腕として補佐をしています。今、選挙は最終局面にあり、残りの 50 票中 30 票を取り込むことができると A は当選するというところまで来ました。ここまでの世論調査では、A さんの投票者の間での支持率は 60% であることがわかっています。さて、A さんが当選する確率はどれぐらいと考えられるでしょうか。
この問題は次のように考えます。
- 試行回数 \(n=50\)
- 成功率 \(p=0.6\)
これらのパラメータを二項分布の確率質量関数に入れて、Python で計算すると以下の通りになります。
from scipy.stats import binom
for i in range(0,51):
print("k=", i, " : ", binom.pmf(i, 50, 0.6))
これをグラフに描いたものが下図です。
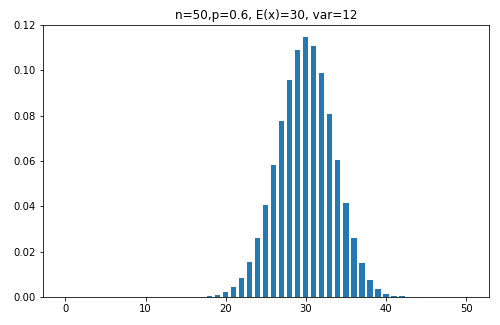
以上のデータから、当選する確率(得票数が 30 以上になる確率)は、対応するそれぞれの棒グラフ(上の表の k=30 以上)を足せば求められるので以下の通りになります。
sum = 0
for i in np.arange(30, 51):
sum += height[i]
sum
このように、たとえ期待値は \(np=50 \cdot 0.6=30\) で当選できそうだと示しているとしても、現状では、正しい当選率は約 56% に過ぎないということがわかります。この数値では、まだ枕を高くして眠ることはできないので、更なる選挙対策をした方が良いと判断できるでしょう。
6.2. 内定率
2 社以上から内定をもらえる確率は?
新しい仕事を探していて、いくつかの本命の会社があるときは、既に複数の内定を貰っていて、それを交渉材料にして本命に挑むのが良い戦略です。さて、X さんは今月、本命の会社のための前哨戦として、1 ヶ月で 7 社の面接を受けることになっています。そして転職エージェントの見積もりでは、X さんは大体 0.2 の確率で内定を貰える素材であると太鼓判をおされています。
今月、X さんが 2 社以上から内定をもらえる確率はどれぐらいあるでしょうか。
この問題は、以下のパラメータをもつ二項分布の問題です。
- 試行回数 \(n=7\)
- 成功率 \(p=0.2\)
これらのパラメータを二項分布の確率質量関数で計算すると以下の通りになります。
from scipy.stats import binom
for i in range(0,8):
print("k=", i, " : ", binom.pmf(i, 7, 0.2))
これを図に描いたものが以下です。X さんが内定を貰う確率は、この二項分布に従います。
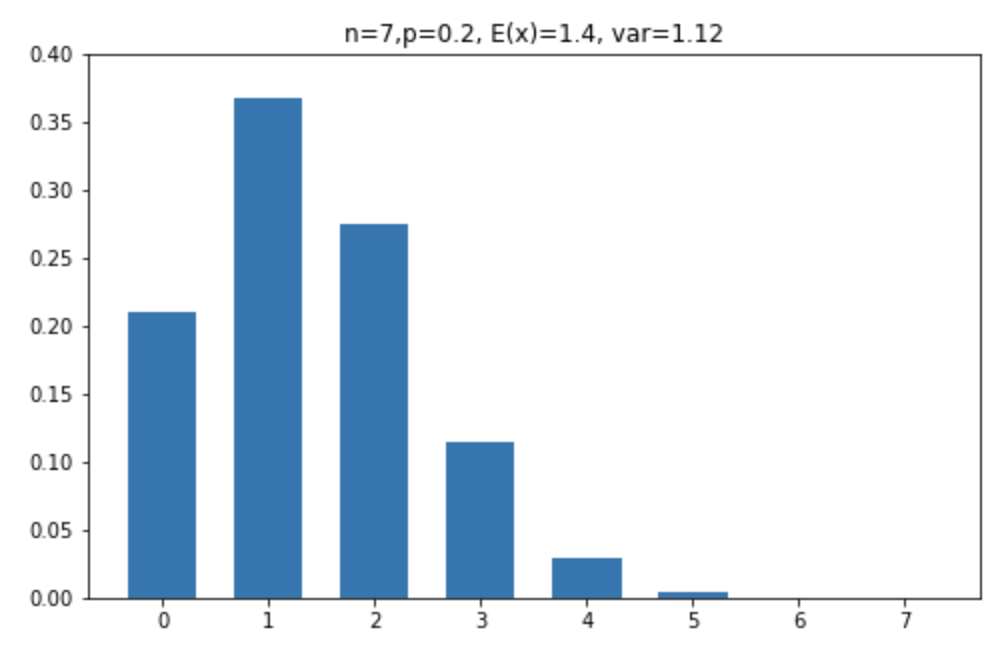
X さんが今月 2 社以上から内定を貰える確率は、これの \(K= 2\) 以上を足したものになので、約 42.3% ということになります。なお X さんが内定を 1 社からも貰えない確率は、約 21.0% もあります。
7. 二項分布のまとめ
最後に内容をまとめておきます。
二項分布とは
「試行回数 n と成功率 p が明らかなときの、成功回数 k の分布」のことです。以下の確率質量関数で求められます。
\[
\rm{Bin}(n,p)
=
\dbinom{n}{k} \ p^k(1-p)^{n-k}
\]
※ \(k\) : 成功数(確率変数), \(n\) : 試行回数, \(p\) : 成功率, \(\binom{n}{k}\) : 二項係数 \({}_nC_{k}\),
二項分布の期待値と分散
二項分布でよく使う分析指標だる期待値と分散は以下の公式で求めることができます。
\[E(X)=np\]
\[\rm{Var}(X)=np(1-p)\]
二項分布と正規分布の近似
二項分布の期待値と分散がともに 5 よりも大きい場合、その二項分布は正規分布に近似します。
以上、最後までご覧頂きありがとうございました。
当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります(コメント返信は余裕ができれば行いたいと考えています)。
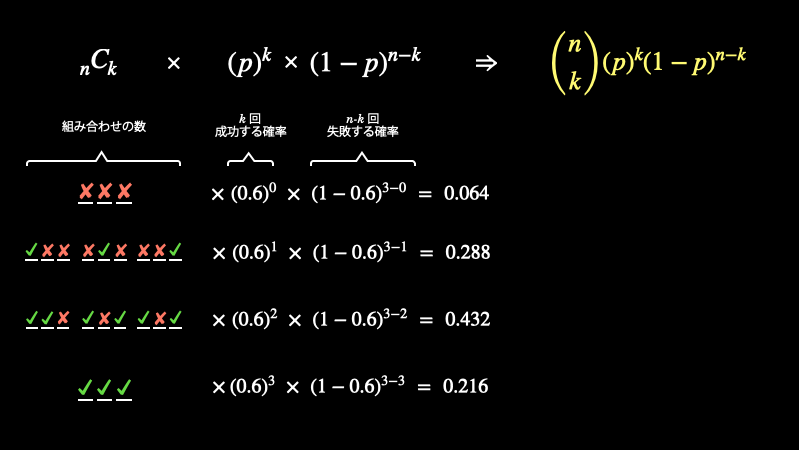

コメント