ベータ分布とは？誰でも理解できるようにわかりやすく解説

ベータ分布は、「成功数 α と失敗数 β が明らかなときの成功率」の連続値型確率分布です。当ページでは、このベータ分布について詳しく解説していきます。具体的には、以下の内容を知ることができます。

それでは早速見ていきましょう。

なお、まだ『確率分布とは？誰でも必ず理解できるようにわかりやすく解説』をご覧になっていない方は、先にそちらをご覧いただいた方が理解しやすくなると思います。

1. ベータ分布とは

ベータ分布は、連続確率分布の一つで、ある試行の成功数 \(α\) と失敗数 \(β\) が分かっている現象の成功率 p の分布を表します。たとえば、コイントスを 100 回行って表 \(α\) が \(60\) 回、裏 \(β\) が \(40\) 回出たとします。このときの成功率（表が出る確率）の分布のグラフは下図の通りになります。

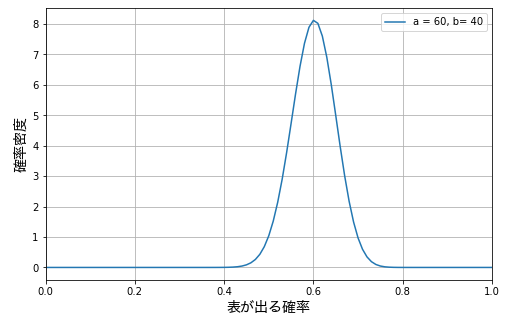
このベータ分布は、表が出る確率は 0.6 である可能性がもっとも高いが、全体としては、表が出る確率は大体 0.45 から0.75 の間と考えられる、ということを示しています。100 回程度の試行では、わかることはこれぐらいです。

それでは試行回数が 10 倍になって、表が出た回数が 600 回、裏が出た回数が 400 回だったらどうでしょう。この場合、ベータ分布のグラフは下図の通りになります。

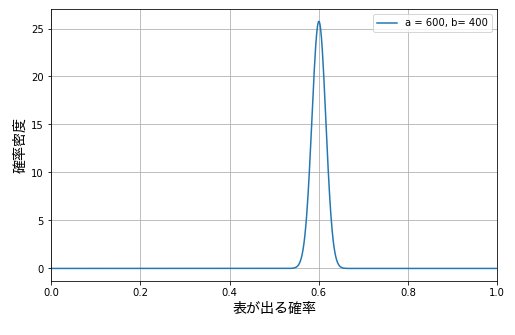
今度はデータが増えたので、このコインで表が出る確率は大体 0.575 から 0.625 の間であるということがわかります。幅が随分と縮まりました。このように、成功数と失敗数から、成功率の分布を得られるのがベータ分布です。

2. ベータ分布の確率密度関数

ベータ分布の確率密度関数は次の通りです。

ガンマ関数の \(\Gamma(z)\) の計算方法は正確には、\(\int_0^{\infty}x^{z-1}e^{-y}dx\) です。しかし、\(\Gamma(z+1)=z\Gamma(z)\) です。\(z\) が正の整数のときは、\(\Gamma(z)=(z-1)!\) で求めることができます。ベータ分布では、パラメータ \(α、β\) は必ず正の整数になります。

3. ベータ分布の期待値（平均値）

ベータ分布の期待値（平均値）は以下の公式で求められます。

例えば、\(α=7, β=3\) のベータ分布の平均値は以下の通りになります。

この成功率を縦の実線で表したものが下図です。

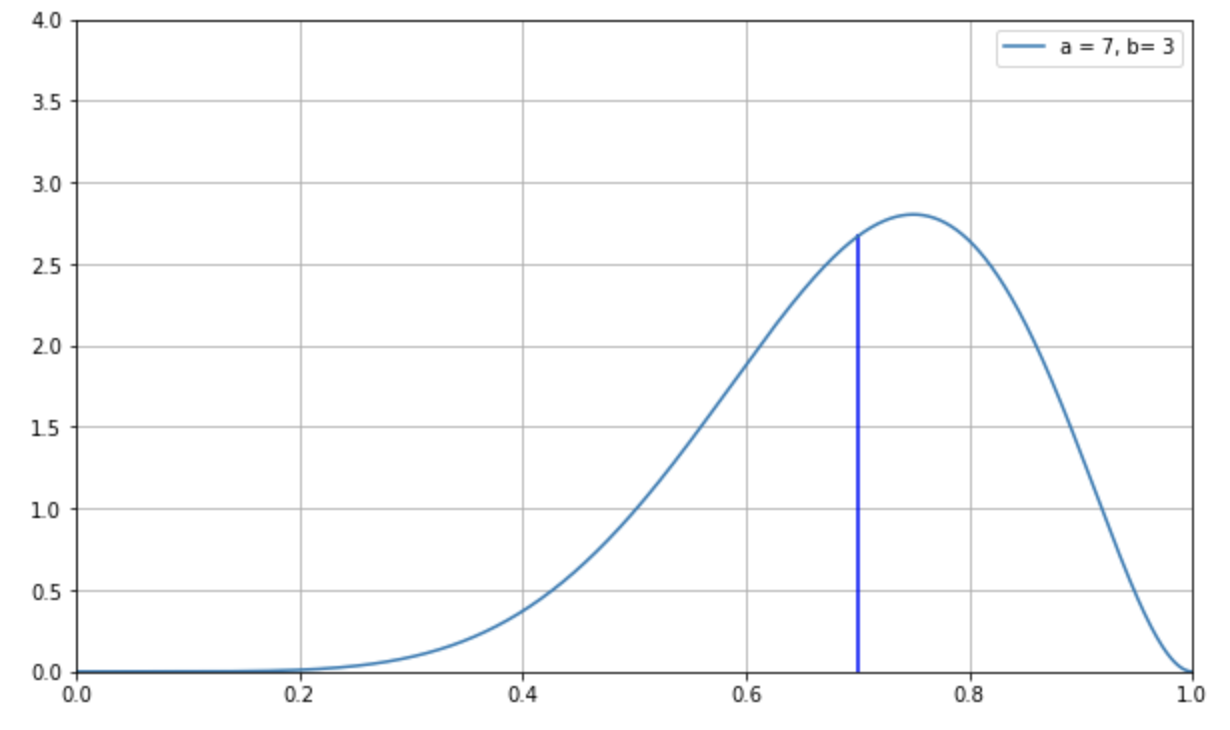
4. ベータ分布の最頻値（中央値）

ベータ分布の最頻値（中央値）は以下の公式で求められます。

最頻値（中央値）は、文字通り、確率変数である成功率 \(p\) のもっともあり得る値（尤もらしい値）のことです。

例えば、\(α=7, β=3\) のベータ分布の平均値は以下の通りになります。

これは成功数 \(α\) が 7 回、失敗数 \(β\) が 3 回という事象を観察したとき、その事象の成功率 \(p\)として、もっともあり得るのは 0.75 であるということを表しています。

この最頻値を縦の破線で表したものが下図です。

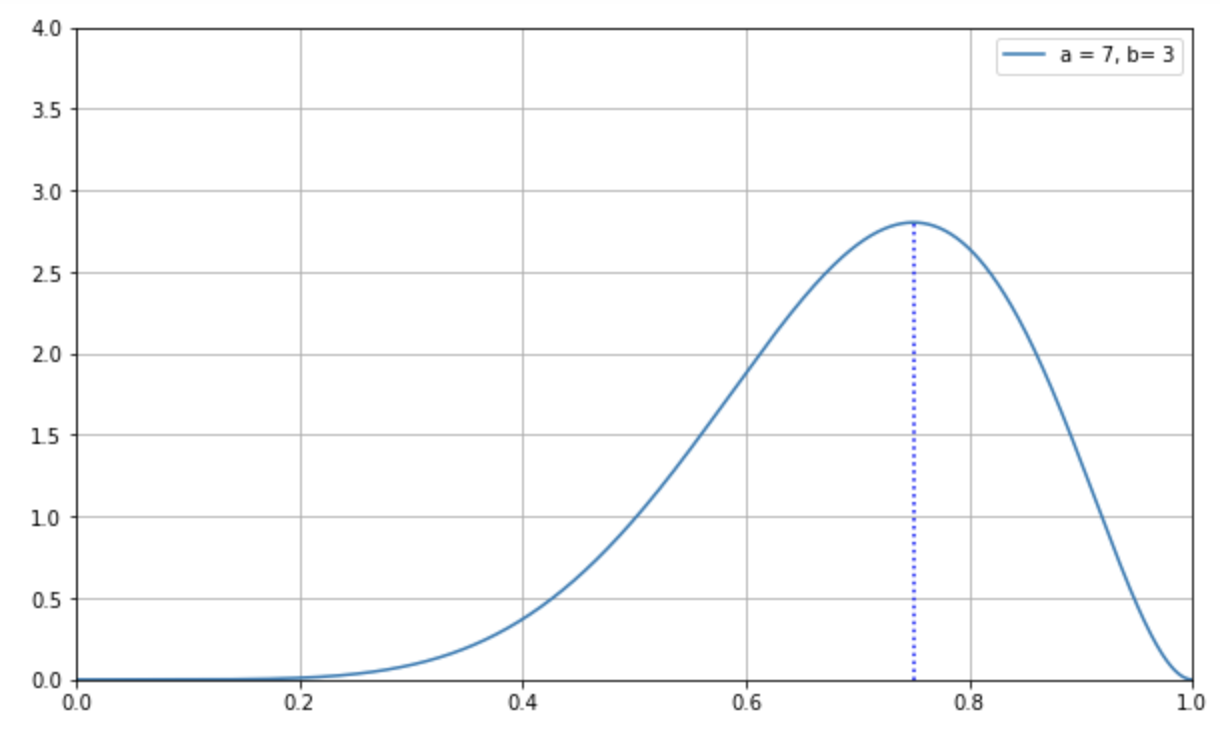
5. ベータ分布の分散

ベータ分布の分散と標準偏差は、以下の公式で求められます。

これはベータ分布の横への広がり具合を表す指標です。

成功数 \(α\) が 7 回、失敗数 \(β\) が 3 回のベータ分布では以下の通りになります。

\[
\rm{Var}(p)
=
\dfrac
{7 \cdot 3}
{(7+3)^2(7+3+1)}
\approx
0.019
\]

\[
\rm{SD}(p)
=
\sqrt{0.019}
\approx
0.44
\]

6. ベータ分布の重要な特徴

ベータ分布は、現在主流の統計学分野であるベイズ統計において特に重要な役割を担っています。その理由の一つが、形状が非常に柔軟であるため、事前確率分布として扱いやすいという点が挙げられます。

どういうことかと言うと、パラメータである成功数 \(α\) と失敗数 \(β\) の値によって、下図の通りグラフの形状が大きく変わるのです（青の実線は平均値・破線は最頻値を示しています）。

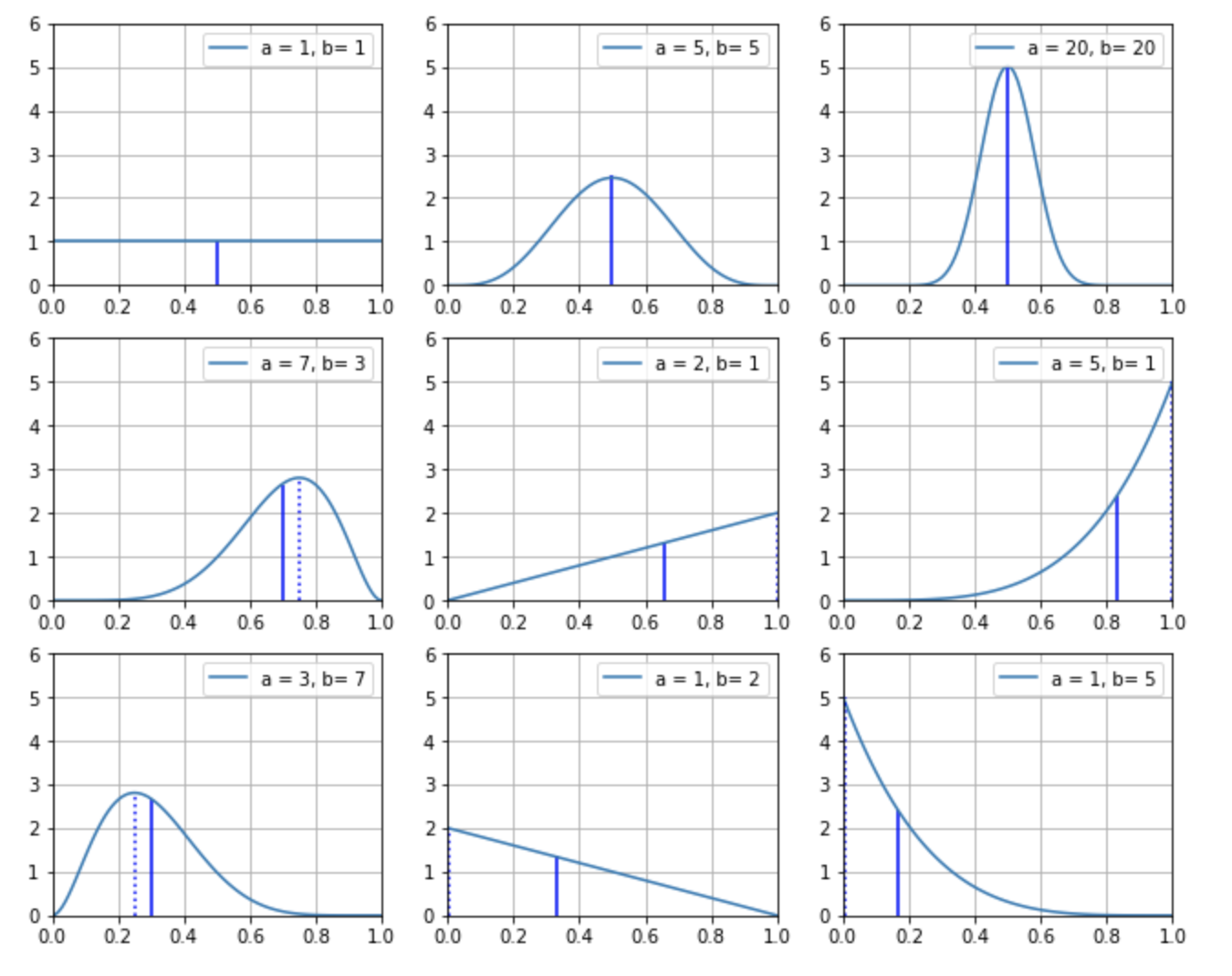
具体的には、ベータ分布は次のような性質になっています。

• \(α=β=1 \) の場合
  　標準一様分布になる。
  　平均値 = 最頻値になる。
• \(α=β>1 \) の場合
  　正規分布になる。
  　平均値 = 最頻値になる。
• \(α>β\) の場合
  　左肩下がりのグラフになる。
  　最頻値が平均値より右側になる。
• \(α<β\) の場合
  　右肩下がりのグラフになる。
  　平均値が最頻値より右側になる。

以上の性質から、ベータ分布はさまざまなものごとを表すのに適しており、ベイズ推定において頻繁に使われるため、重要な地位を占めています。

7. ベータ分布がよくわかる問題

以上がベータ分布ですが、それだけだと実用のイメージが湧かないと思いますので、ベータ分布の有用性がよくわかる例を解説します。早速、見ていきましょう。

7.1. レビュー評価が最も高いのは？

レビュー評価が最も良いのはどれ？

ベイズ統計に関する本で何か良いものはないか探していた X さんは、Amazon のレビューを参考に、購入候補を以下の 2 つにまで絞り込みました。

• 本 A：22 個中 20 個が肯定的なレビュー
• 本 B：101 個中 95 個が肯定的なレビュー

この 2 つのうち、X さんが購入した後に、肯定的なレビューを書き込む可能性（X さんが満足する可能性）がもっとも高いものはどれでしょうか。

このような場合に、まず思い浮かぶのは、以下のように、肯定的なレビューの数をレビューの総数で割ったもので比較することです。

このように比較すれば、断然、本 B の方が良さそうに見えます。

しかし、この単純な比較方法には違和感があります。それぞれの合計レビュー数（サンプル数）が大きく異なるからです。もっと良い方法はないでしょうか？そう、こういう時こそベータ分布の出番です。

肯定的なレビューの数を成功数 \(α\)、否定的なレビューの数を失敗数 \(β\) として、上述の確率密度関数に当てはめて、それぞれ確率分布グラフを描くと、下図のようになります。

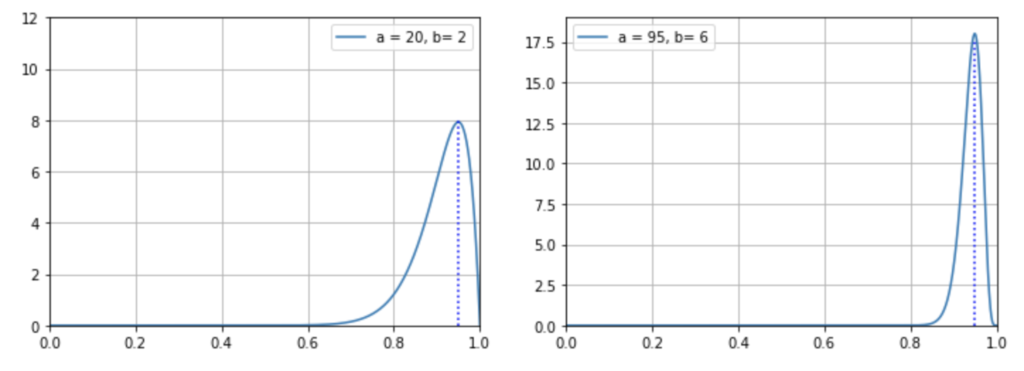
これがベータ分布のグラフです。

このグラフの横軸は、確率変数である成功率 \(p\)（肯定的なレビューを貰える確率）です。そして縦軸は、確率密度です。このグラフ下の任意の範囲の面積が、その範囲に確率変数が収まる確率を意味します。2 つのグラフの縦軸の目盛りの違いは気にする必要はありません。ベータ分布のグラフにおいて、大事なのは曲線下の面積の割合だからです。

このベータ分布のグラフを使うと、さまざまな分析が可能になります。その一つが最頻値（中央値）です。これは以下の公式で求められます。

これをそれぞれで計算すると以下の通りになります。

先ほどとは違って、今度は、ほんのわずかにですが本 A の方が良いということになりました。なお、この最頻値の値は次のように解釈してください。

• 本 A：20 個の肯定的なレビューと、2 個の否定的なレビューがある場合、その本が肯定的なレビューを得る確率として最もあり得る可能性が高い（尤もらしい）のは、95 % である。
• 本 B：95 個の肯定的なレビューと、6 個の否定的なレビューがある場合、その本が肯定的なレビューを得る確率として、もっともあり得る可能性が高い（尤もらしい）のは、約 94.9 % である。

以上のことから、わずかな違いながら本 A の方が満足する可能性が高いという結論を導き出すことができます。

7.2. 当たりが出る確率は？

2 本目が当たる確率

駄菓子屋でアイスバーを買ったら、時々、当たりが出て 2 本目が貰えます。しかし駄菓子屋のおばちゃんに、当たりの確率を聞いても、おばちゃんも知らないようです。そこで過去のデータを調べてもらったところ、この 1 週間では 40 本が売れて、その中に当たりは 10 本だったことがわかりました。

さて、このアイスバーで、当たりが出る確率が 20-30% の範囲に収まる確率はどれぐらいあるでしょうか？

この問題を、ベータ分布の確率密度関数に当てはめると以下の通りになります。

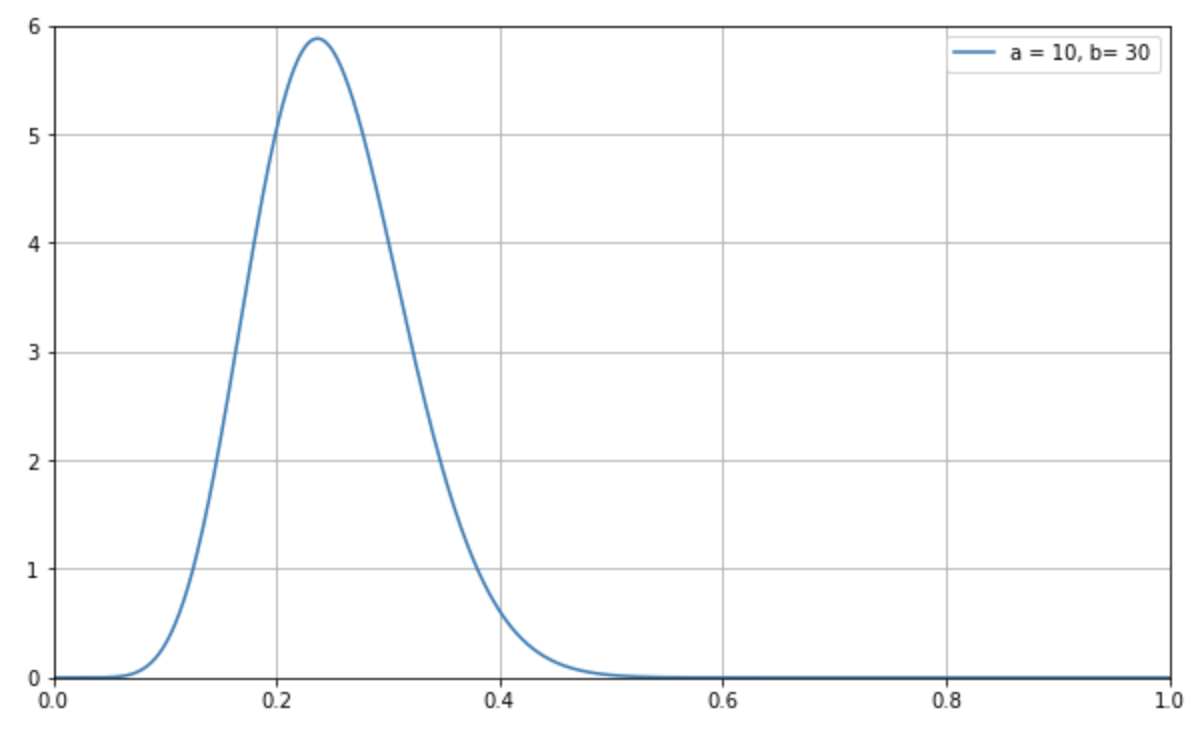
この確率密度関数において、成功率が \(p\) = 0.20 ~ 0.30 の間におさまる可能性を求めてみましょう。これは以下の方法で算出できます。なお、積分については『積分とは何か？最もわかりやすく簡単に理解できるように解説』で解説しているので、ぜひご覧ください。

このように、アイスバーで当たり棒が出る確率が 0.20 ~ 0.30 の間におさまる可能性は 53.45% あるということがわかりました。 ベータ分布を使うと、このように、ある事象の成功確率が、任意の範囲内にどの程度の可能性でおさまるのかを求めることも可能になります。

なお、上のような積分は手計算ではとてもできるものではありません。必ずプログラミングで解きます。例えば、Python で解くと以下のように出てきます。

from sympy import *
from scipy.special import beta, gamma

p = symbols("p")
f=((p**(10-1))*((1-p)**(30-1)))/beta(10,30)
print(integrate(f, (p, 0.2, 0.3)))

0.534510799689322

まとめ

最後にあらためて内容をまとめておきます。

ベータ分布とは

ベータ分布は、成功数 \(α\) と失敗数 \(β\) が明らかなときに、それらのデータから、もっともあり得る（尤もらしい）成功率 \(p\) を導き出すことを可能とし、さらに、その成功率 \(p\) に関する様々な分析（ \(p\) の最頻値や \(p\) が任意の範囲に収まる確率などの導出など）を可能とする連続確率分布です。

ベータ分布の重要な公式

ベータ分布を使いこなす上で重要な公式は以下の通りです。

確率密度関数

期待値（平均値）

\[E(p) = \dfrac{\alpha}{\alpha+\beta}\]

最頻値（中央値）

\[\rm{Mode}(p)= \dfrac{\alpha-1}{\alpha+\beta-2}, (\alpha,\beta>1)\]

分散と標準偏差

\[
\rm{Var}(p)
=
\dfrac
{\alpha\beta}
{(\alpha+\beta)^2(\alpha+\beta+1)}
\]

\[
\rm{SD}(p)
:=
\sqrt{\rm{Var}(\pi)}
\]

最後までご覧頂きありがとうございました。

当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります（コメント返信は余裕ができれば行いたいと考えています）。