確率分布を誰でも理解できるようにわかりやすく解説

確率分布は、簡潔に言うと「ある試行で起こり得るすべての事象の確率を出力する関数」です。現実世界の実に様々な現象を、確率分布一つで表すことができるため、特に統計学の世界で非常に重宝されています。

このページでは、この確率分布についてわかりやすく解説していきます。特に以下のようなことが理解できるようになります。

それでは始めましょう。

1. 確率分布とは

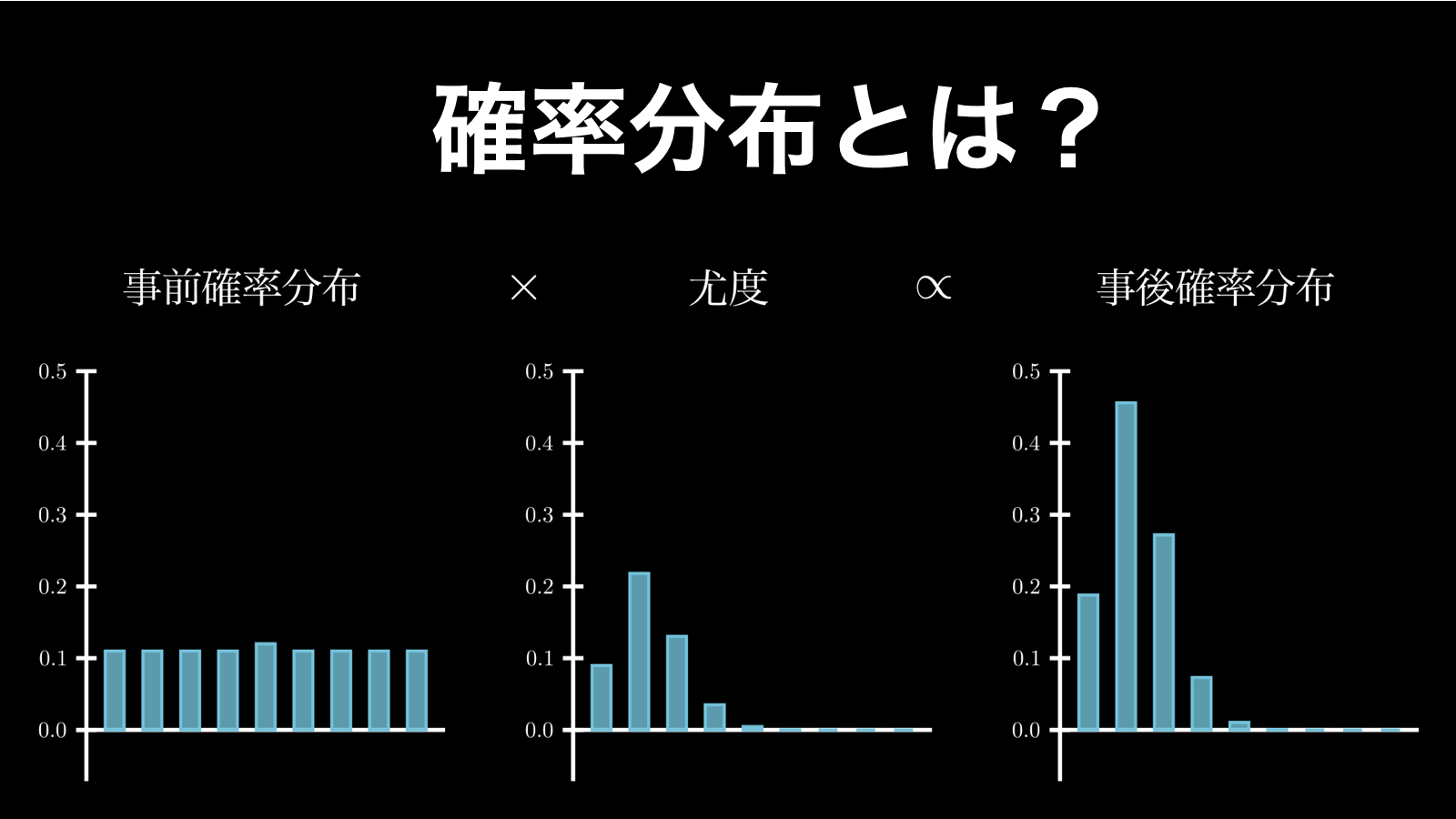
確率分布（probability distribution）は、簡潔に言うと、下図で示している通り、「ある試行で起こり得るすべての事象の確率を出力する関数」のことです。

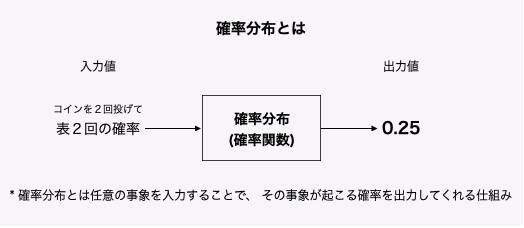
ただし、普通の関数と確率分布（確率関数）は違いがあります。その一つが変数と確率変数の違いです。

1.1. 確率変数とは

普通の関数はよく \(y=f(x)=x^2\) というように表されます。これは入力値 \(x\) の値に応じた出力値 \(y\) を計算して返すものであることを意味しています。

ご覧のように普通の関数では、入力値 \(x\) と出力値 \(y\) はどちらも実数です。このときの入力値 \(x\) のことを変数と言います。

対照的に、確率関数では、変数は実数ではなく事象です。

例としてコイントスで考えてみましょう。コイントスを 1 回行ったとき、起こりうる全ての事象は「表が出る」「裏が出る」の 2 つです。この事象が、確率分布（確率関数）の入力値です。しかし、いちいち \(p({\small 表が出る})\)、\(p({\small 裏が出る})\) というように表すのは面倒です。

そこで、「表が出る \(\rightarrow 1\) 」「裏が出る \(\rightarrow 0\) 」のように、それぞれの事象を数値で表します。そして、この数値を \(p(1), \ p(0)\) というように関数に渡します。そうすると、対象となる事象の確率が返ってきます。

*定義式の部分（\(0.5^x(1-0.5)^{1-x}\) の部分）については後ほど解説します。

このように事象を数値で表したものが確率変数（random variable）です。そして、\(0, 1, 2\) などの実現した事象を示す値を実現値（realization）と言います。

なお、ある試行における事象は大文字の \(X\) で表します。そして、個別の具体的な事象は小文字の \(x\) で表します。そのため、たとえば「表が出る確率」は \(p(1)\) と表したり、\(p(X=1)\) と表したりします。最初は煩わしく感じますが、慣れるまでの辛抱です。

1.2. 確率分布のグラフ

確率分布はグラフで見ると、とてもわかりやすくなります。

たとえばコイントスを 2 回行ったとき、起こりうる全ての事象は、「表が 2 回出る（ \(2\) とする）」「表が 1 回裏が 1 回出る（ \(1\) とする）」「裏 2 が回出る（ \(0\) とする）」の 3 つです。別の確率分布 \(p(y)\) に、それぞれの事象を入力すると、次のように、それぞれが起こる確率が返されます。

*定義式の部分（\(\binom{2}{k}0.5^k(1-0.5)^{2-k}\) の部分）については後ほど解説します。

この確率変数を横軸、確率を縦軸にしてプロットしたものが確率分布のグラフです（厳密には縦軸は確率質量と言います。確率質量×離散値の等差幅＝確率です）。

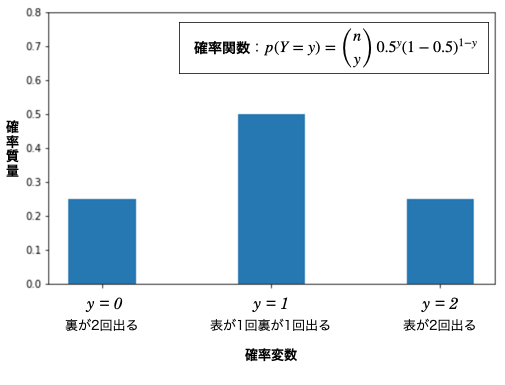
このようにグラフにすると、コイントスを 2 回行った場合、\(y=1\) の確率、つまり表が 1 回裏が 1 回出る確率がもっとも高いことや、\(y=0, 2\) の確率、つまり裏が 2 回出る確率と、表が 2 回出る確率が同じであることなど、この試行に関する確率が視覚的にとても把握しやすくなります。

このことから確率分布はグラフで描かれるのが一般的です。

2. 離散確率分布と連続確率分布

確率分布は、大きく次の 2 つに分けられます。

• 離散型確率分布：確率変数が離散値の確率分布。棒グラフで表される。
  （代表例：ベルヌーイ分布、二項分布、ポアソン分布）
• 連続確率分布：確率変数が連続値の確率分布。線グラフで表される。
  （代表例：ベータ分布、ガンマ分布、正規分布）

なお、離散値は、\(0, 1, 2\) や \(0.1, 0.2, 0.3\) のように連続していない数値の並びのことで、連続値とは切れ目なく連続している実数のことです。

それぞれより詳しく見ていきましょう。

2.1. 離散型確率分布

離散型確率分布は、その名の通り、確率変数が離散値の確率分布です。勘の良い方はお気づきかと思いますが、ここまで見てきたコイントスに関する確率分布は、離散型確率分布です。

確率変数を \(Y\) で表すとしたら、コイントスを 2 回投げる試行の例では、表が 2 回出るという事象が \(Y=2\)、表が 1 回裏が 1 回出るという事象が \(Y=1\)、裏が 2 回出るという事象が \(Y=0\) でした。

この通り確率変数の実現値が \(0, 1, 2\) の離散値なので、離散型確率分布です。そして、これをグラフに描くと棒グラフになります。もう一度見返してみましょう。

なお、離散型確率分布ではグラフの縦軸は確率質量です。そして、「確率質量 × 離散値の等差 = 任意の地点での確率」となります。上図では、等差は \(1\) なので、\(y=0, 1, 2\) となる確率はそれぞれ \(0.25 \times 1=0.25\)、\(0.50 \times 1=0.50\)、 \(0.25 \times 1=0.25\) となります。

そして確率の総和は常に \(1\) なので、これらを足し合わせると \(0.25+0.50+0.25=1.00\) となります。また例えば、「\(y=0\) または \(y=1\) となる確率」は両者の足し算で、\(0.25 + 0.50 =0.75\) というように求められます。

以上が離散型確率分布です。

2.2. 連続型確率分布

連続型確率分布は、確率変数が連続値の確率分布です。たとえば、ベータ分布というものがあります。これは成功数 \(\alpha\) と失敗数 \(\beta\) が明らかであるときの確率変数である成功の確率 \(\pi\) の分布です。

確率は離散値ではなく、連続値ですから、当然ベータ分布は連続型確率分布です。実際に \(\alpha = 7, \beta=3\) として、このベータ分布をグラフに描くと、下図の通り線グラフになっていることがわかります。

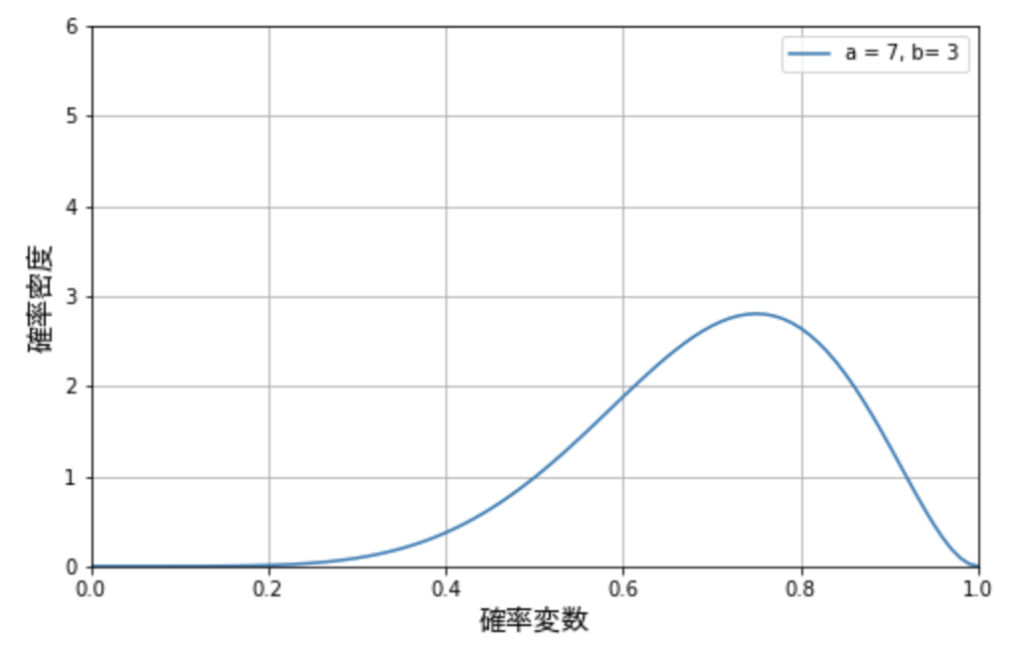
連続型確率分布では、グラフの縦軸は確率密度になっています。そしてグラフの線の下の面積が確率になっており、それは積分で求めることができます。たとえば、このグラフの横軸 \(0.6 \sim 0.7\) における面積は約 \(0.25\) になります。これが、この試行における成功率が 60%から70% の範囲に収まる確率ということになります。

連続確率分布は、グラフの線の下の総面積は必ず \(1\) になります。そして連続確率分布では、積分をすることで、値が任意の範囲に収まる確率を求めます。

ただし、すべての確率分布で累積分布関数という、任意の範囲の面積を求めるための関数が用意されているため、これを使えば実際は積分の知識がなくても面積を計算することは可能です。

ちなみに積分については『積分とは何かを誰でも理解できるようにわかりやすく解説』で詳しく解説していますので、ご興味があれば、ぜひご確認ください。

3. 確率分布の指標

ある確率分布が、どのような性質を持っているのかを理解するために、必ず使う指標が期待値と分散です。この 2 つについて解説しておきます。

3.1. 期待値

期待値（expectation value）は、「確率変数の実現値の平均」を表す指標です。よりわかりやすく言うと、「その試行を繰り返し行うと、最終的に確率変数がどの値に収束して行くのか」を表す指標です。記号では Expectation の頭文字をとって \({\rm E }[X]\) と表されます。

例として以下の画像では期待値を青の実線で示しています。そして比較として最頻値（その試行を繰り返し行うと、もっとも見られる確率変数）を破線で示しています。

これは以下の計算で求めることができます。

たとえば、コイントスを 1 回行ったときの確率変数の期待値は以下の通りに計算できます。

確率変数は \(1\) で「表が出る」、\(0\) で「裏が出る」なので、\(\dfrac{1}{2}\) という期待値は 「表と裏が同じぐらい出る」と解釈できます。

続いて、コイントスを 2 回行ったときの確率変数の期待値は以下の通りです。

これは、コイントスを 2 回行ったら、実現値 \(1\) の事象である「表が 1 回裏が 1 回出る（順不同）」という事象が最も期待できることを表しています。

なお実際には、それぞれの確率分布で、期待値を求めるための公式が用意されていますので、もっと簡単に計算することができます。これについては、後ほど確率分布の種類を解説するところで紹介します。

以上が確率分布の期待値です。

3.2. 分散

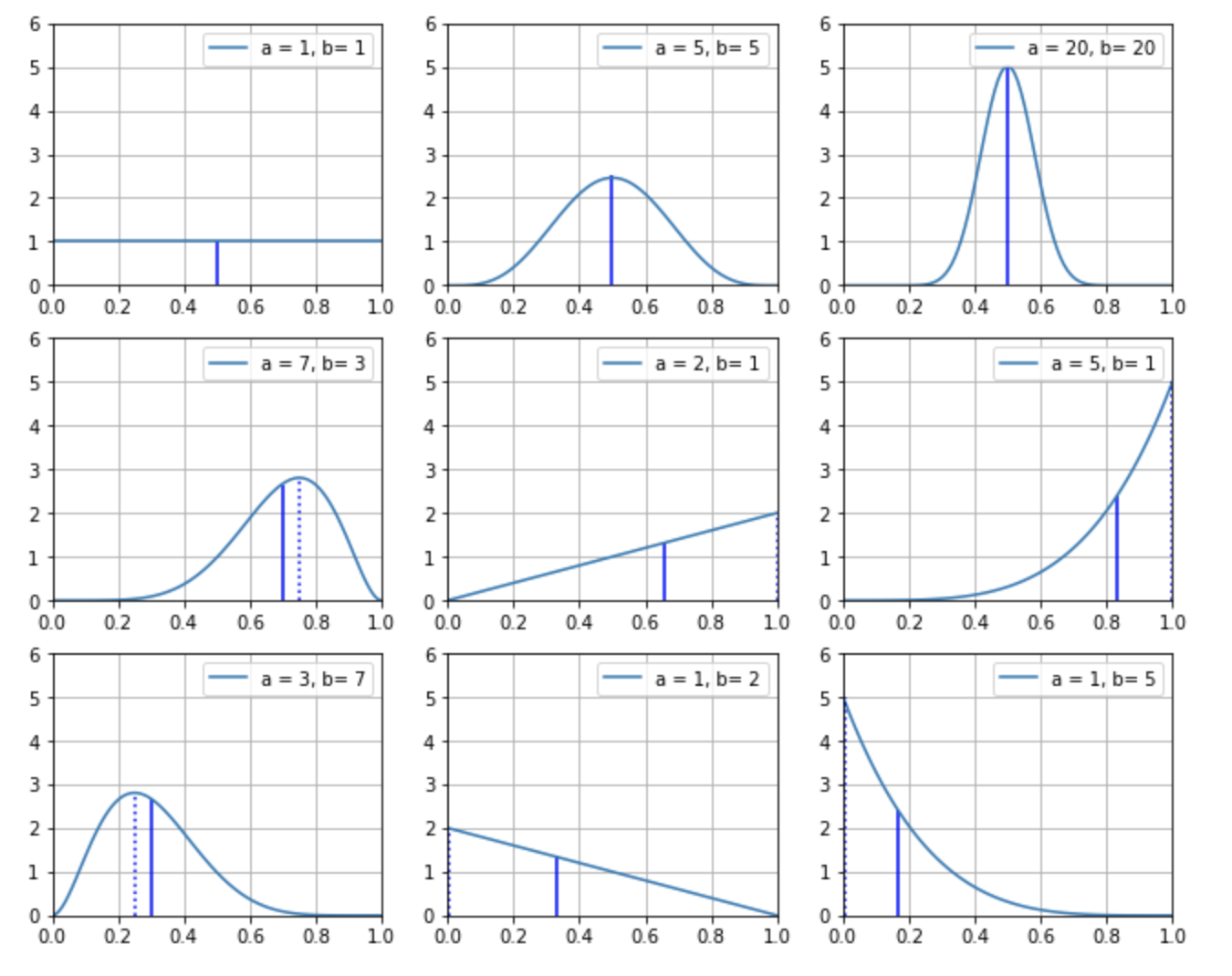
分散（variance）とは確率のばらつき具合のことで、グラフの横方向への広がり具合を示す指標です。記号では \({\rm V}[X]\) と表します。実際にグラフで確認してみましょう。下図は異なる分散のグラフの比較図です。

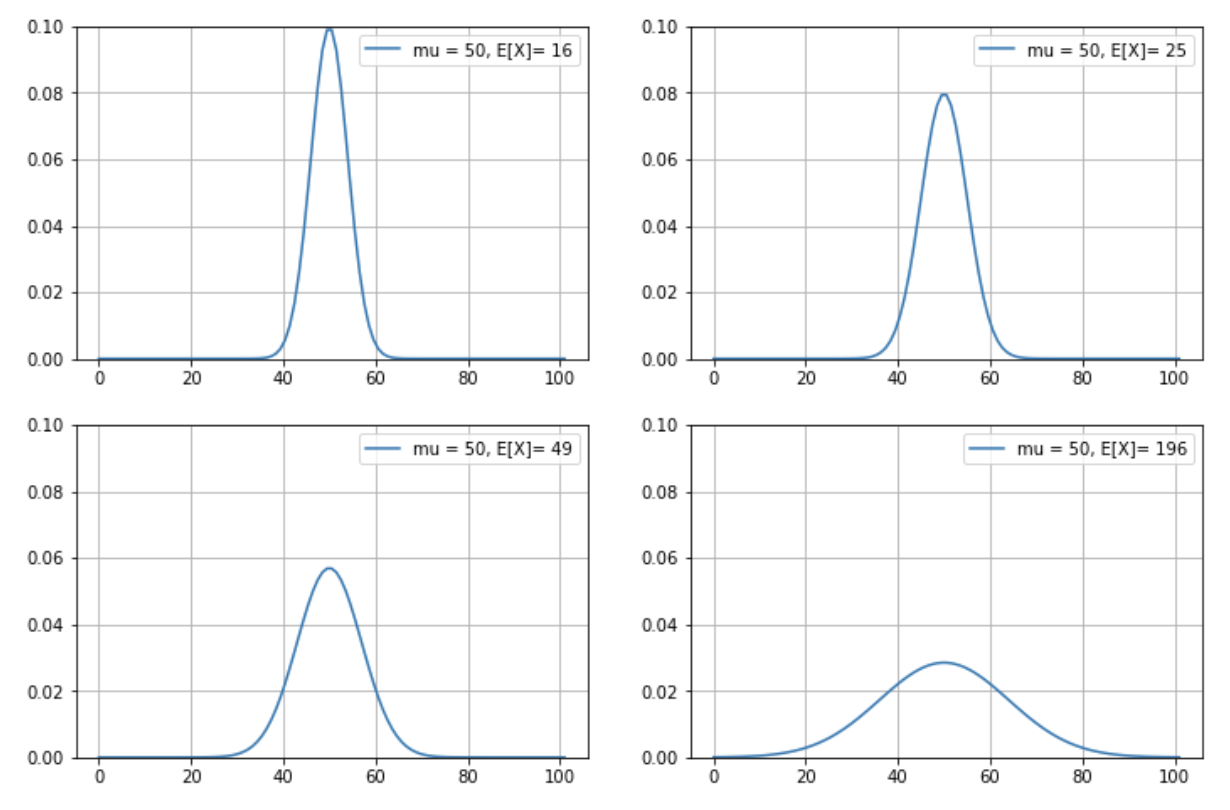
ご覧のように分散が小さいほど、横方向への広がりが小さく、頂点が高くなります。反対に、分散が大きいほど、横方向への広がりが大きく、頂点が低くなります。

この分散は以下の計算で求めることができます。

以下の計算もこれと同じことです。

たとえば、コイントスを 1 回行う試行の確率変数の分散は、以下の通りになります。

実際には、それぞれの確率分布で、分散を求めるための公式が用意されていますので、もっと簡単に計算することができます。これについては、すぐ後ほどで紹介します。

3.3. 期待値と分散の公式 6 つ

期待値と分散には以下の公式があります。詳細は割愛しますが、頭に入れておくと良いでしょう。

1. \({\rm E}(a)=a\)
2. \({\rm E}[X+Y]={\rm E}[X]+{\rm E}[Y] \)
3. \(\alpha {\rm E} [X] = {\rm E}[\alpha X]\)
4. \({\rm E}[XY]={\rm E}[X]{\rm E}[Y]\)
5. \({\rm V}[aX+b]=a^2 {\rm V}[X]\)
6. \({\rm V}[X+Y]={\rm V}[X]+{\rm V}[Y]\)

4. 確率分布の種類

ここではよく使う代表的な確率分布を 7 つ解説します。それぞれの確率関数や期待値・分散の求め方だけでなく、現実のどのような現象を表す確率分布なのかも、グラフを添えて解説していますのでイメージがつきやすいと思います。

それでは見ていきましょう。

4.1. ベルヌーイ分布

ベルヌーイ分布は、確率分布の中でもっともシンプルなものです。具体的には、コイントスのように起こりうる結果が成功か失敗かの 2 つのみの試行の成功率の分布を表す離散型確率分布です。

確率関数	\(f(k|p)=p^k(1-p)^{1-k}\)
累積分布関数	\( \begin{cases} 0 & {\rm for} k < 0 \\ 1-p & {\rm for} 0 ≤ k < 1 \\ 1 & {\rm for} k ≥1 \end{cases} \)
期待値	\(E(X)=p\)
分散	\(V(X)=p(1-p)\)

上のコインの例では、イカサマコインでなければ表が出る確率も裏が出る確率も \(0.5\) です。しかし、現実世界では、このような確率は分かっていないことが多いです。たとえば、ある病気の新薬ができたとします。これを患者に投与して、治癒したという事象 \((x=1)\)、治癒しなかったという事象 \((x=0)\) を観察するとします。

このとき治癒率が \(0.7\) だとしたら、治癒 \((x=1)\) と非治癒 \((x=0)\) の割合は以下の通りになるはずです。

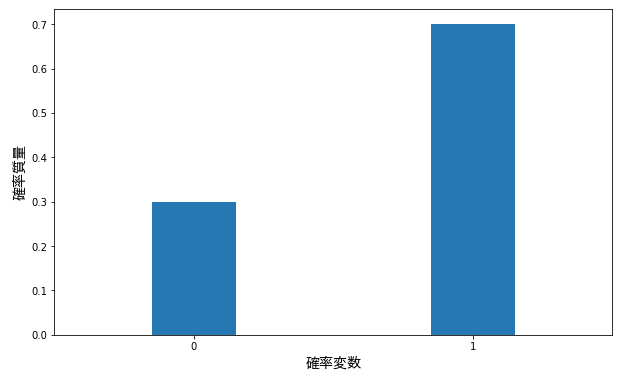
このように 2 本の棒グラフになるのがベルヌーイ分布の特徴です。より詳しくは『ベルヌーイ分布を誰でも理解できるようにわかりやすく解説』で解説しているので、ぜひご確認ください。

4.2. 二項分布

二項分布は、離散型確率分布の一つで、試行回数 \(n\) と成功率 \(p\) が明らかなときの成功回数 \(k\) の分布」です。

確率関数	\(f(k|n, p)=\dbinom{n}{k}p^k(1-p)^{n-k}\)
累積分布関数	\( \displaystyle I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor ) \)
期待値	\(E(X)=np\)
分散	\(V(X)=np(1-p)\)

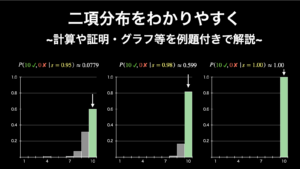
たとえばバスケットボールのフリースローを考えてみてください。フリースロー成功率が 70% の選手が 10 回フリースローを行ったとしたら、成功数の分布は下図の二項分布のグラフの通りになります。

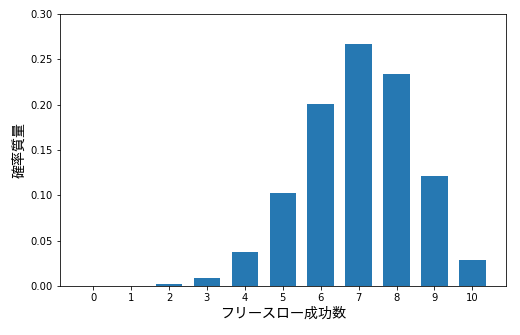
より詳しくは『二項分布を誰でも理解できるようにわかりやすく解説』で解説しています。

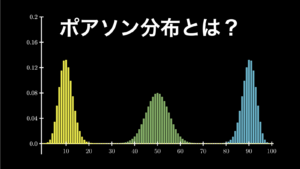
4.3. ポアソン分布

ポアソン分布は、二項分布を変形したもので、簡単に言うと、「起こる確率が \(\lambda\) の、滅多に起こらない出来事が、任意の時間（面積や回数でも可）当たりに起こる回数 \(k\) を表す確率分布」です。訪問営業での成約数やゴルフのホールインワンの成功数など、起こる確率がとても小さいものをイメージするとわかりやすいでしょう。

確率関数	\( f(k|\lambda)= \displaystyle {\frac {\lambda ^{k}}{k!}}\cdot e^{-\lambda } \)
累積分布関数	\( {\displaystyle e^{-\lambda }\sum {i=0}^{k}{\frac {\lambda ^{i}}{i!}}}\)
期待値	\(E(X)=\lambda\)
分散	\(V(X)=\lambda\)

たとえば、ある営業マンの訪問営業の成約率が \(λ=3\) だったとしたら、実際に 100 件を訪問したときの成約数の分布は以下の通りになります。

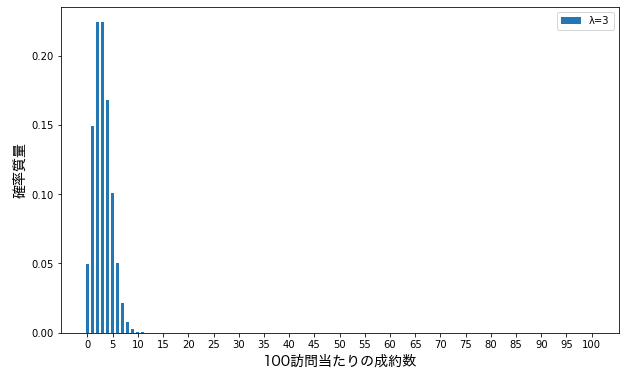
このように見てみると、制約数は最低 0 件から最大 10 件程度まで見込めることがわかります。

ポアソン分布は他にも、単位時間当たりの詐欺電話の数や、単位面積当たりのトルコ料理屋の数、単位回数当たりのホールインワン数など、様々な、稀にしか起こらない現象の起こる回数の確率を知るのに役立ちます。

より詳しくは『ポアソン分布とは？誰でも理解できるようにわかりやすく解説』で解説しています。

4.4. 一様分布

一様分布は、ある試行のすべての事象が起こる確率が同じである場合の確率分布で、離散型でもあり連続型でもあります。ベイズ統計において、事前分布に関する情報が何もない場合に使われるという点で有用です。

確率関数	\( f(x|α,β) = \dfrac{1}{β-α} \) * 確率変数の範囲を \(α≤x≤β\) とする
期待値	\(E(X)=\dfrac{\alpha + \beta}{2}\)
分散	\(V(X)=\dfrac{1}{12}(\beta – \alpha)^2\)

たとえばスイカ割りのために、目隠しをしたままグルグル回され、デタラメに止まるとすると、止まった角度が北から右に何度であるかは、0 から 360 の範囲の連続一様分布で表すことができます。

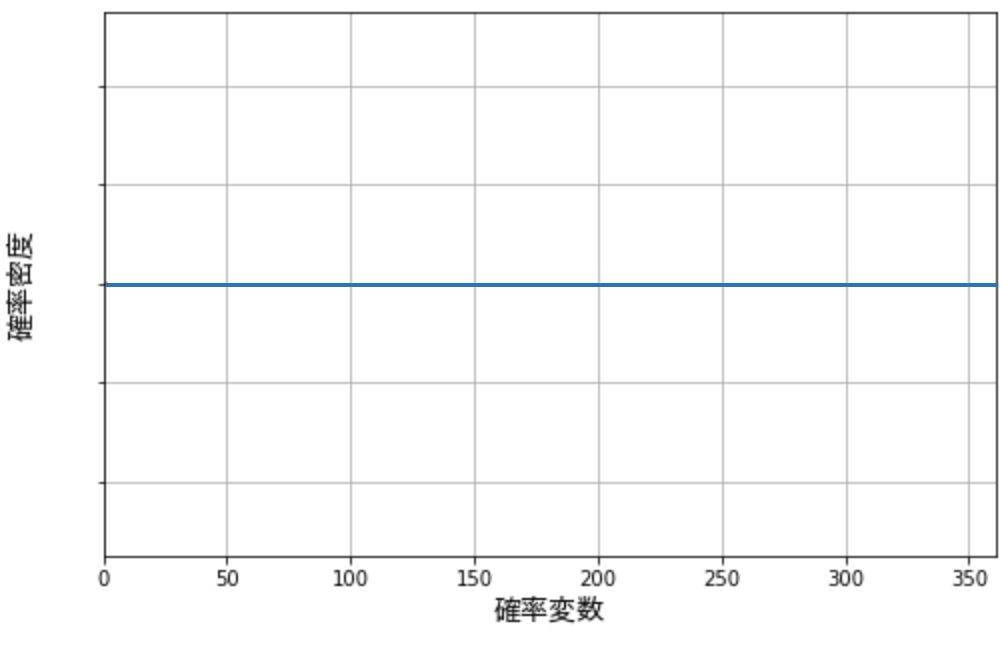
このように水平なグラフを描くのが一様分布です。より詳しくは『一様分布を誰でも理解できるようにわかりやすく解説』で解説しています。

4.5. ベータ分布

ベータ分布は、「成功数 \(α\) と失敗数 \(β\) が明らかなときの成功率 \(p\)」の連続値型確率分布です。

確率関数	\( f(p|\alpha, \beta) {\displaystyle {\frac {p^{\alpha -1}(1-p)^{\beta -1}}{\operatorname {B} (\alpha ,\beta )}}} \)
累積分布関数	\( {\displaystyle I_{x}(\alpha ,\beta )} \)
期待値	\( {\displaystyle \operatorname {E} [X]={\frac {\alpha }{\alpha +\beta }}} \)
分散	\( {\displaystyle \operatorname {V} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}} \)

たとえば、コイントスを 100 回行って表 α が 60 回、裏 βが 40 回出たとします。このときの成功率（表が出る確率）の分布のグラフは下図の通りになります。

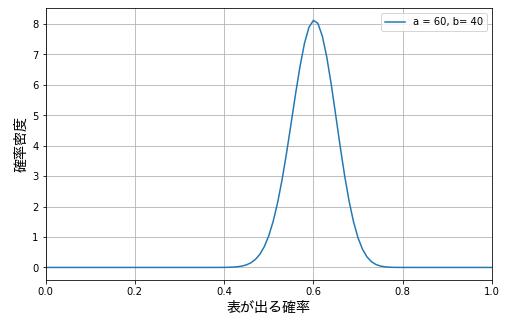
このベータ分布は、表が出る確率は 0.6 である可能性がもっとも高いが、全体としては、表が出る確率は大体 0.45 から0.75 の間と考えられる、ということを示しています。100 回程度の試行では、わかることはこれぐらいです。

より詳しくは『ベータ分布とは？誰でも理解できるようにわかりやすく解説』で解説しています。

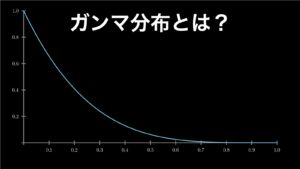
4.6. ガンマ分布

ガンマ分布は、「任意の単位時間や単位面積 λ の間に 1 回起きることが期待できる出来事が、実際に起きるまでの時間の分布」です。

確率関数	\( {\displaystyle {\frac {1}{\Gamma (k)\,\theta ^{k}}}x^{k-1}e^{-x/\theta }={\frac {\lambda ^{k}}{\Gamma (k)}}x^{k-1}e^{-\lambda x}} \)
累積分布関数	\( {\displaystyle {\frac {\gamma (k,x/\theta )}{\Gamma (k)}}={\frac {\gamma (k,\lambda x)}{\Gamma (k)}}} \)
期待値	\( {\displaystyle k\theta ={\frac {k}{\lambda }}} \)
分散	\( {\displaystyle k\theta ^{2}={\frac {k}{\lambda ^{2}}}} \)

たとえば製品寿命が 10 年の （\(\lambda=10\)）電子部品があるとします。この電子部品が実際に壊れるまでの期間は、以下のガンマ分布に従います。

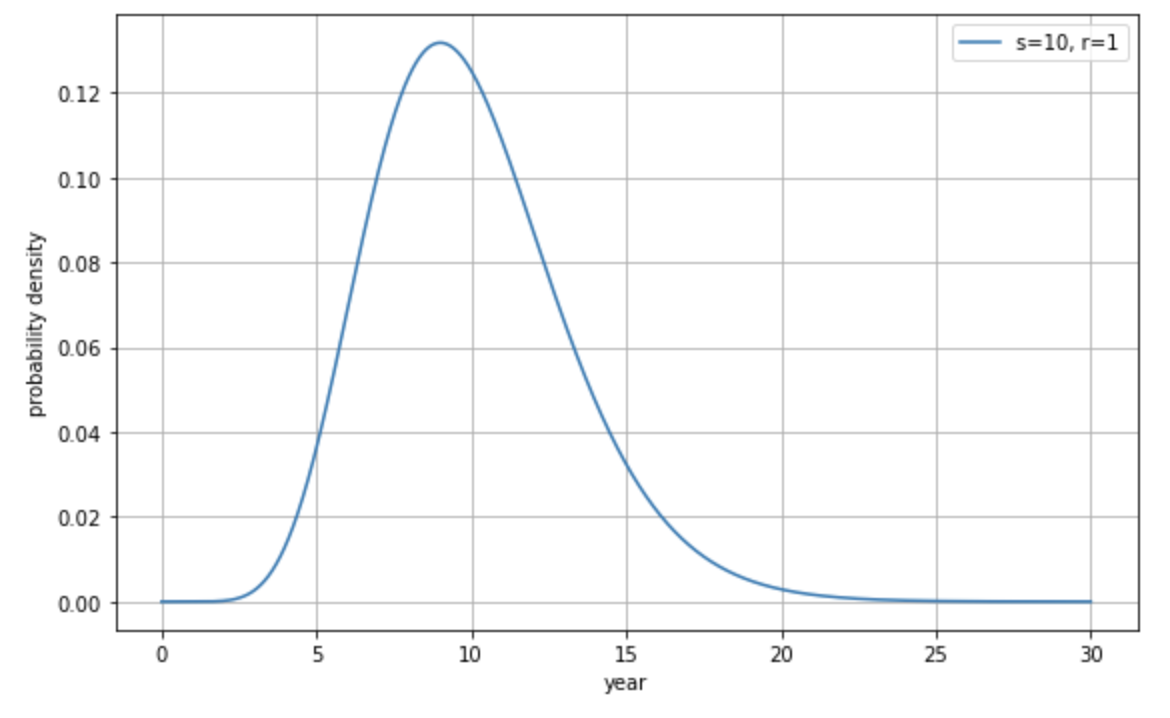
こうやって見てみると寿命が 10 年と言っても、5 年で壊れる場合もあれば、から 20 年経っても壊れない場合もあるということがわかります。このように稀にしか起こらない出来事が実際に起こるまでの期間の分布を示すのがガンマ分布です。

4.7. 正規分布

正規分布は、「平均 \(\mu\) と分散 \(\sigma^2\) がわかっているときに、様々なデータを明らかにしてくれる分布」です。身長や体重・テストの点数など、身の回りの多くの連続確率変数が、正規分布に従っているとされています。

確率関数	\( f(x|\mu, \sigma)= {\displaystyle {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)} \)
累積分布関数	\( {\displaystyle {\frac {1}{2}}\left(1+\operatorname {erf} \,{\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)} \)
期待値	\( \mu \)
分散	\( \sigma^2 \)

たとえば成人男性の身長が平均 170 cm で、標準偏差（√分散=\(\sigma\)）が 7 だとしたら、身長の分布は下図のようになります。

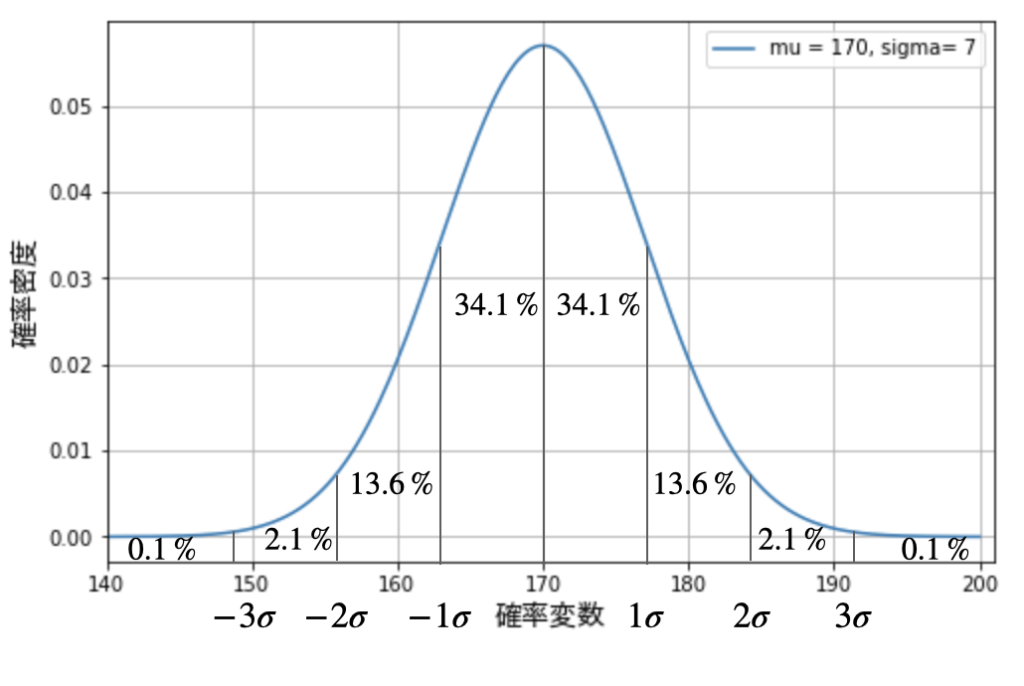
上図で示している通り、正規分布には重要な性質があります。それは確率変数（ここでは身長）が、平均値 \(\mu\) から \(± 1 \sigma\) 以内にデータの 68.2% が収まり、\(± 2 \sigma\) 以内に 95.4% が収まり、 \(± 3 \sigma\) 以内に 99.8% が収まるというものです。

このことから男性の身長が、163cm ~ 177 cm に収まる可能性が 68.2%、156 cm ~ 184 cm に収まる可能性が 95.4% であるというように判断できます。他にも、例えば 191 cm 以上となる確率は 0.1% であるということになります（*このデータは実際のデータではありません）。

以上が正規分布です。

5. まとめ

最後にあらためて内容を軽くまとめておきましょう。

確率分布は「ある試行で起こり得るすべての事象の確率を出力する関数」です。大きく分けて離散確率分布と連続確率分布の 2 種類があります。前者の定義式を確率質量関数、後者の定義式を確率密度関数と言います。

離散確率分布とは

離散確率分布は確率変数が離散値の確率分布のことです。これをグラフにすると棒グラフになります。確率“質量”関数と呼ばれるのはそのためです。離散確率分布では、それぞれの確率変数における確率を足し算することによって、確率の総和を求めることができます。確率の総和はもちろん 1 です。

連続確率分布とは

連続確率分布は、確率変数が連続値の確率分布のことです。これをグラフにすると曲線グラフになります。曲線下の面積が確率を表しており、確率“密度”関数と呼ばれるのはそのためです。連続確率分布では、曲線下の任意の範囲の面積を積分によって求めることで、確率がその範囲に収まる確率（確率の確率）を求めることができます。曲線下の面積の総和は 1 になります。

以上が確率関数のまとめです。最後までご覧頂きありがとうございます。当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります（コメント返信は余裕ができれば行いたいと考えています）。