共役事前分布とは？誰でも理解できるようにわかりやすく解説

2021 11/07

2021年10月17日 2021年11月7日

共役事前分布とは、連続型確率分布を使ったベイズ推定の計算を簡単にしてくれるものです。

『ベイズ推定とは？誰でも理解できるようにわかりやすく解説』では、離散型確率分布を例にベイズ推定の計算を行いましたが、これの連続値バージョンとお考え頂くと良いでしょう。ただし、連続型確率分布同士では、基本的に計算はあまりにも複雑になります。その問題を解決してくれるのが共役分布です。

さらに共役分布を使うと、事前分布と事後分布が同じ種類の確率分布になるので、比較が簡単になるというメリットもあります。

現在では、ベイズ推定はマルコフ連鎖モンテカルロ法（MCMC）を使って行うので、共役分布を使う機会はありません。しかし原理をわかった上で MCMC を使うのか、何もわからないまま機械的に MCMC を使うのか、では大きな違いがあります。

そこで当ページでは、共役事前分布について詳しく解説していきます。具体的には、以下のことを学ぶことができます。

当ページで学べること

ベイズ推定を連続確率分布で計算する方法（共役族）がわかる。
共役事前分布とは何か、そのメリットは何か、デメリットは何かが具体的にわかる。
代表的な 3 つの共役事前分布（ベータ–二項モデル・ガンマ−ポアソンモデル・正規−正規モデル）を深く理解することができる。
ガンマ−ポアソンモデル、正規−正規モデルを例題を解きながら深く理解することができる。

それでは早速始めましょう。なお、このページを読み進める前に、以下の 2 つのページを確認しておくことをオススメします。

1. 共役事前分布とは

共役事前分布はベイズ推定を行う上で非常に便利な事前確率分布のことです。具体的には、ベイズ推定において共役事前分布を使うと、以下の 2 つの大きなメリットを享受できます。

計算が非常に簡便になる（積分の計算を行う必要がなくなる）
事前モデルと事後モデルの比較が簡単になる（両者の確率分布が同じになる）

通常、ベイズ推定において、事前分布も尤度関数も連続型確率分布である場合は、計算が複雑過ぎて分析など不可能なものになってしまいます。しかし共役事前分布を使うと、それらが簡単になるのです。

さて、この共役事前分布を文章で定義するなら、以下のように言うことができます。

共役事前分布とは

パラメータ \(\theta\) を持つ事前確率分布 \(f(\theta)\) があるとします。そして、\(\theta\) という条件下でデータ \(d\) を観察することの尤度を \(f(d|\theta)\) とします。このとき事後モデルが、\(f(\theta|d) \propto f(\theta)f(d|\theta)\) となるような \(f(\theta)\) を「共役事前分布」と言います。

この説明ではわからないと思いますので、具体例を見ていきましょう。

2. 代表的な 3 つの共役族

共役族の組み合わせは全てを説明し切れないほどの数がありますが、ベイズ統計において代表的なのは次の 3 つです。

ベータ−二項分布共役族
ガンマ−ポアソン分布共役族
正規−正規分布共役族

ここでは、それぞれの場合の事後モデルの求め方と例題を一つずつ見ながら、解説していきたいと思います。

2.1. ベータ−二項分布共役族

ベータ−二項分布共役族では、事前確率分布がベータ分布、尤度関数が二項分布、事後確率分布がベータ分布になります

のパラメータが成功数 \(\alpha\) と失敗数 \(\beta\) で、データの尤度関数モデルのパラメータが試行回数 \(n\) と成功率 \(p\) のとき、事後の正規分布モデルは以下の通りになります。

ベータ分布−二項分布共役族

\[\begin{eqnarray}
&{\small 事前}&: {\rm Beta}(\alpha, \beta) \\
&{\small 尤度}&: {\rm Bin}(n, p) \\
&{\small 事後}&: {\rm Beta}(\alpha+x, \beta+n-x)
\end{eqnarray}\]

具体例で確認しましょう。以下の問題をご覧ください。

問題：支持率 \(\pi\) の事後確立

日本では原則 4 年に一度、衆議院議員選挙（衆院選）があります。そして Z 氏が、衆院選への出馬を決めたとします。あなたは彼のための政治アナリストとして雇われました。

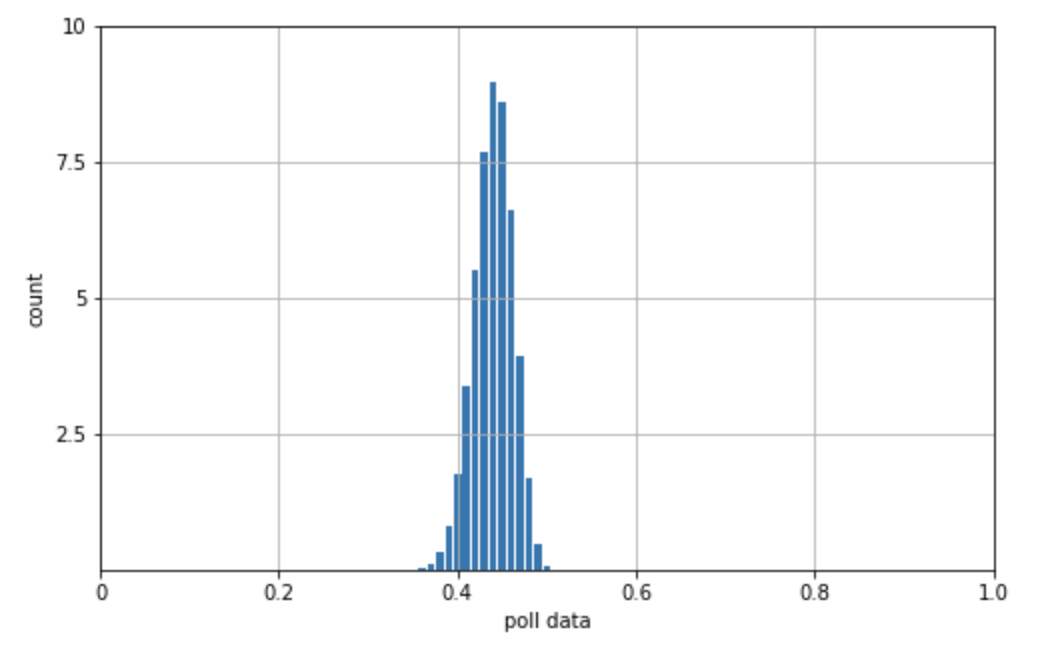
あなたはアナリストとして、これまで 30 回、X 氏の支持率の調査を行っています。その調査によると、 Z 氏の支持率は 45 % を最頻値として、最小 35% から最大 55% の間を行ったり来たりしていることがわかりました。二項分布で表すと下図 1a. の通りです。

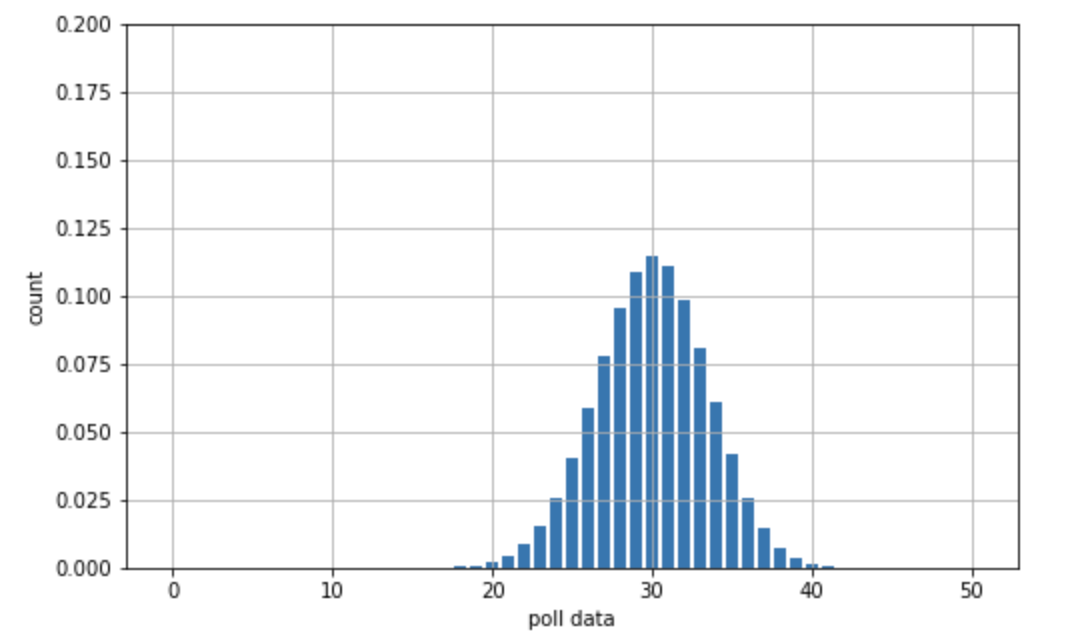
そして様々なキャンペーンを行ってきて、今、選挙は最後の大一番です。そこで、あなたは、現時点での支持率を把握するために、最後の調査として n=50 人のランダムな有権者の中で、Z 氏を支持する人の数 Y を記録しました。結果、Y = 30 （有権者のうち 6 割が Z 氏を支持している）であることがわかりました。この新しいデータは、試行回数:n, 成功数:Yをパラメータとする二項分布で表すことができます。

図 1b. 最後の支持率調査で Z 氏を支持すると答える人数 \(Y\) の確率分布 \(n=50\)

さて、この事前に行われた 30 の事前調査と、直近に行った調査のデータを踏まえた上で、Z 氏の支持率はどれぐらいあると考えられるでしょうか。

早速、この問題について考えてみましょう。なお、記号の意味は、それぞれ以下のようになっています。

支持率 \(\pi\)：Z 氏を支持している人の割合
データ \(Y\) ：Z 氏を支持する人の数
事前確率 \(f(\pi)\)：変数を支持率 \(\pi\) とする確率密度関数
尤度関数 \(f(y|\pi)\)：支持率が \(\pi\) の時に、 50 人中 30 人が Z 氏を支持すると答えるというデータを観察することの尤もらしさを求める関数
事後確率 \(f(\pi|y)\)：データを踏まえた状態で、Z 市の当選率を求める確率密度関数

そして、ベイズ推定の公式は以下の通りです。

ベイズ推定の公式

\[\begin{eqnarray}
\overset{\small (事後確率分布)}{f(\pi|y)}
=
\dfrac{
\overset{(事前確率分布)}{f(\pi)}
\overset{(尤度関数)}{f(y|\pi)}
}
{
\underset{(正規化定数)}{f(y)}
}
\end{eqnarray}\]

それでは見ていきましょう。

2.1.1. 事前ベータ分布モデル

ベイズ推定は、まず事前確率分布 \(f(\pi)\) を求めることから始めます。

この問題における事前確率は、「新しいデータを観察する前の、Z 氏の支持率 \(\pi\) の確率」です。そして事前確率分布は、「\(\pi\) を確率変数とする確率密度関数 \(f(\pi)\) 」です。この事前確率分布は、次の 2 つのステップで求められます。

事前モデルとして用いる確率分布を決める
選んだ確率分布のパラメータを調整する

今回のケースでは、事前確率分布 \(f(\pi)\) は、どの確率密度関数で表せるでしょうか。結論から言うと、ベータ分布が最も適しています。このように「確率変数 \(\pi\) をベータ分布で表す」ということを、記号では以下のように書きます。

\[\pi \sim \rm{Beta}(α,β)\]

*「確率変数 \(\pi\) をベータ分布で表す」という意味

それでは他にも確率分布はある中で、なぜ、ベータ分布が適していると言えるのでしょうか。その理由は、今回の問題では、データ（=尤度関数）の \(f(y|\pi)\) が二項分布で表されるものだからです。

他にも、データがポアソン分布なら事前確率分布はガンマ分布を選びますし、データが正規分布なら事前確率分布も正規分布を選びます。これらは共役きょうやくという関係にあり、この組み合わせを選ぶと計算が楽になるのです。

さて、それでは事前確率分布をベータ分布で表すとして、パラメータはどうすればよいでしょうか。今回、事前情報は明らかに、図 1. で示した “過去に行われた合計 30 回分の X 氏の支持率調査”ですので、これと同じような形状になるように調整すれば良いのです。そして、そのためにはベータ分布の代表的な分析指標である、期待値や標準偏差を使います。

詳しく解説していきます。

まず、事前情報である図 1a. から、以下のことがわかっています。

(1) \(\pi\) の最頻値は 0.45
(2) \(\pi\) は最小値 0.35 から最大値 0.55 の間

(1) から、　\(\pi\) の期待値は 0.45 であることがわかります。そしてベータ分布では期待値は、以下の公式で求められます。

\[E(\pi)=\dfrac{α}{α+β}\]

このことから、\(E(\pi) \approx 0.45\) となるようなパラメータを選べば良いということが分かります。これは次のようにアレンジして示すことができます。

\[α \approx \dfrac{9}{11}β\]

次に (2) から、ベータ分布のグラフが最小値 0.35 から最大値 0.55 の間辺りに収まるようにすれば良いことがわかります。

この条件でいくつかプログラミングでトライ&エラーを行うと、最終的に、以下の確率密度関数が、事前モデルとして適しているということを導き出せます。

\[\pi=\rm{Beta}(45,55)\]

この連続確率分布をグラフに描いたものが下図 2. です。

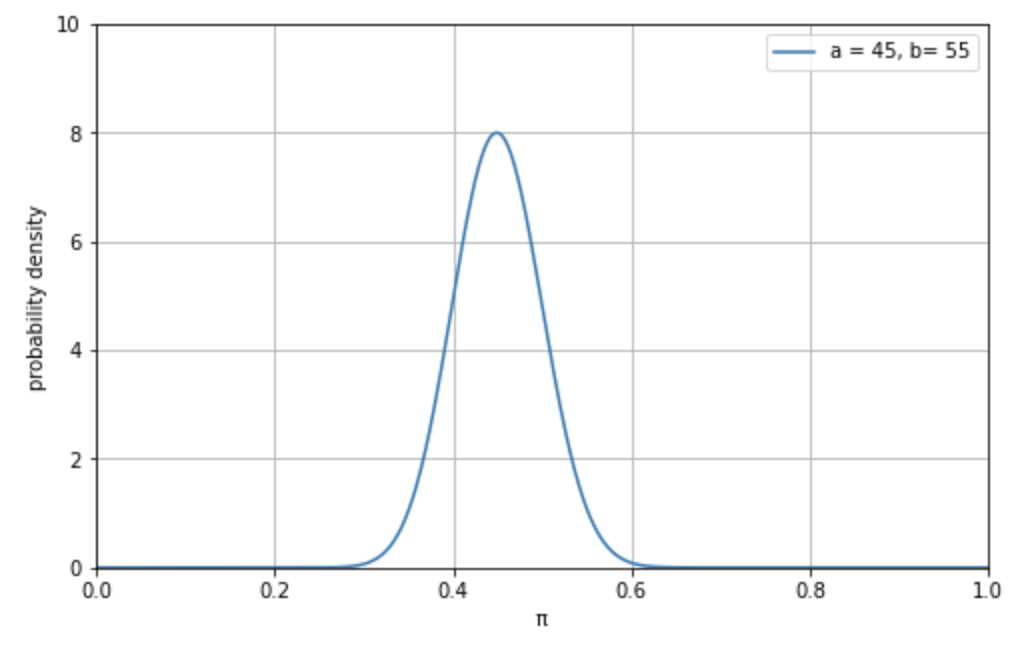
\[\pi \sim \rm{Beta}(45,55)\]

\[
f(\pi) =
\dfrac
{\Gamma(100)}
{\Gamma(45)\Gamma(55)}
\pi^{44}(1-\pi)^{54}\]

これが事前確率分布です。

2.1.2. 二項尤度関数モデル

続いて尤度関数 \(f(y|\pi)\) を求めます。

今回の問題では、最新の調査で、Z 氏を支持すると答えた有権者の数は 50 人中 30 人であることがわかっています。そのため、尤度関数は \(f(y=30|\pi)\) となります。これは「Z 氏の支持率が変数 \(\pi\) であるときに、50人中 y=30 人が Z 氏を支持すると答えることの尤もらしさ」を意味します。

問題文から分かる通り、この尤度関数は、二項分布の確率質量関数で表せることがわかります。

\[Y|\pi \sim \rm{Bin}(50, \pi)\]

以上のことから尤度 \(f(y|\pi)\) の確率質量関数は以下の通りになります。

\[f(y|\pi)=P(Y=y|\pi)=\dbinom{50}{y}\pi^{y}(1-\pi)^{50-y}\]

この確率質量関数は、「もし Z 氏の支持率が \(\pi\) だった場合に、50 名中 30 名が彼を支持すると答えることの尤もらしさ」を示すものです。これをわかりやすくプロットしたものが下図 1.2. です。

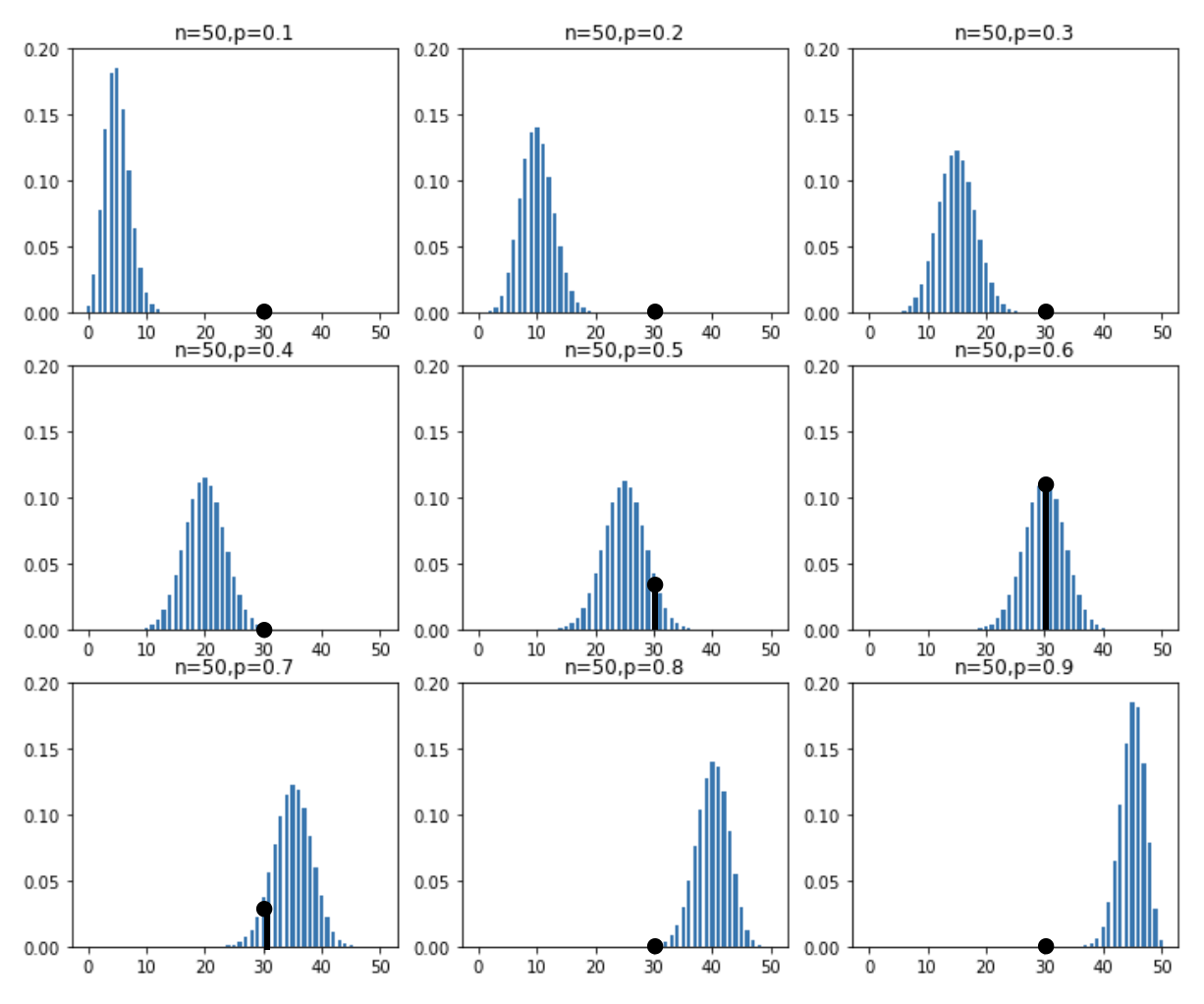
図 1.2.2.a \(Bin(50,\pi)\) の確率質量関数 \(f(y|\pi)\) のグラフ \(\pi \in {0.1, 0.2, …, 0.9}\) 。\(Y=30\) の位置を黒い点と線で表示

図中では、\(y=30\) となる点を、黒の点と線で表しています。これによって、尤度がわかりやすくなります。具体的には、 \(n=50, p=0.1\) と \(n=50, p=0.9\) の場合は尤度はゼロに近く、そこから \(n=50, p=0.6\) に近づくにつれて尤度は高くなっていることが分かります。そして、この尤度を \(\pi=0.1\) から \(0.9\) で、それぞれ計算したものが以下のコードです。

In [1]:

from scipy.stats import binom
for i in range(0,10):
        print("π=", i/10,", y=", 30, " : ", binom.pmf(30, 50, i/10))

π= 0.0 , y= 30  :  0.0
π= 0.1 , y= 30  :  5.729811958109521e-18
π= 0.2 , y= 30  :  5.834313885677648e-10
π= 0.3 , y= 30  :  7.742632078387694e-06
π= 0.4 , y= 30  :  0.0019866205710076714
π= 0.5 , y= 30  :  0.04185914925255199
π= 0.6 , y= 30  :  0.11455855282952349
π= 0.7 , y= 30  :  0.03703876313329532
π= 0.8 , y= 30  :  0.0006117721516988336
π= 0.9 , y= 30  :  1.9978618956199384e-08

尤度関数は、これらの尤度（上図 1.2 の黒い点と線）だけを抜き出し、一つのグラフにプロットして、連続値に打ち直したものです。下図で示している通りです。

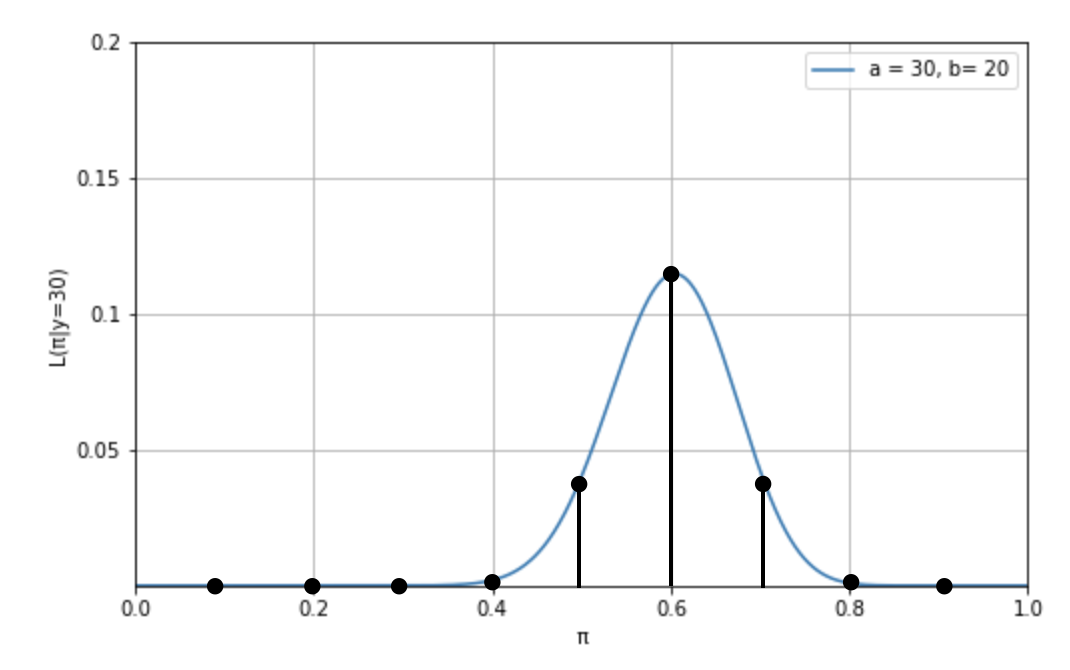
この尤度関数からは、Z 氏の支持率は最低 30% から 90% の間のどこかにあるということがわかります。

\[y=30|\pi\sim\rm{Bin}(50,\pi)\]

\[
f(y=30|\pi) =
\dbinom{50}{30}\pi^{30}(1-\pi)^{20}
\]

2.1.3. 事後ベータ分布モデル

ここまでで事前確率分布と尤度関数（データ）が揃いました。もう一度、両者をグラフで見てみましょう。

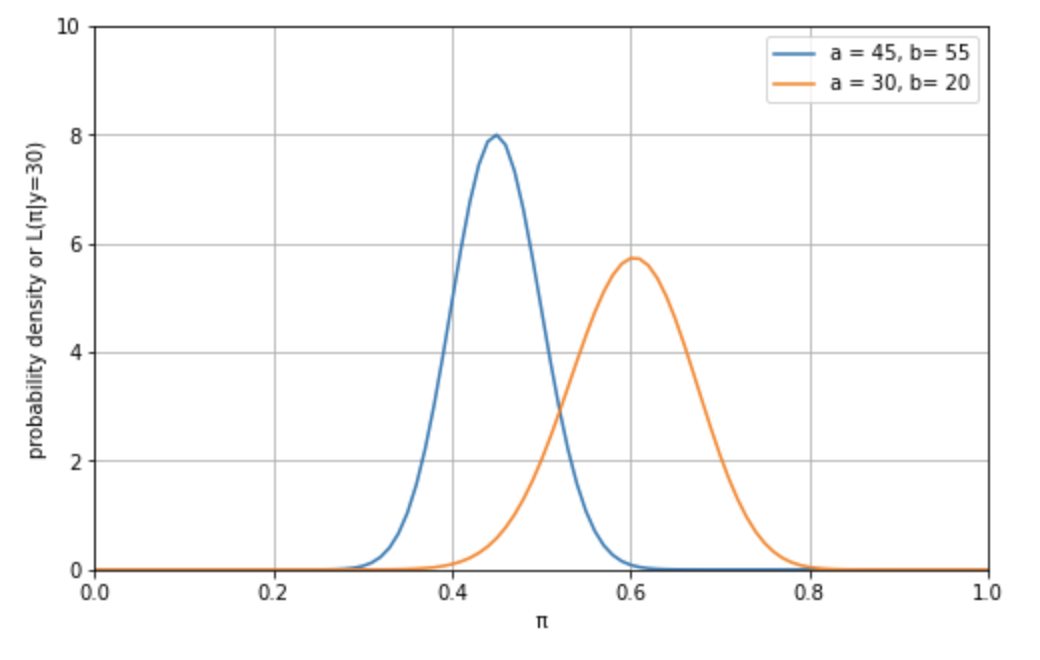
図 1.3.a. \(\pi\) の事前確率分布（青）と、\(\pi, y=30 of n=50\) の尤度関数（オレンジ）

青が \(\pi\) （Z 氏の支持率）の事前確率分布です。オレンジが、それぞれの \(\pi\) において、Z 氏を支持する人の数が 50 人中30人であることの尤もらしさを示す尤度関数です。

こうやって両者を比較すると、以前のデータから作った事前確率分布と、新しいデータから作った（尤度関数）はお互いに、完全に同意していないことがわかります。具体的には、事前確率分布は、最近のデータよりも、Z 氏の支持率を低く見積もっているようです。

さて、それではこれらの確率分布を組み合わせたら、どのような事後確率分布モデルが導き出されるでしょうか。答えは以下です。事後確率分布、事前確率分布と尤度関数の間に挟まれる形になります。

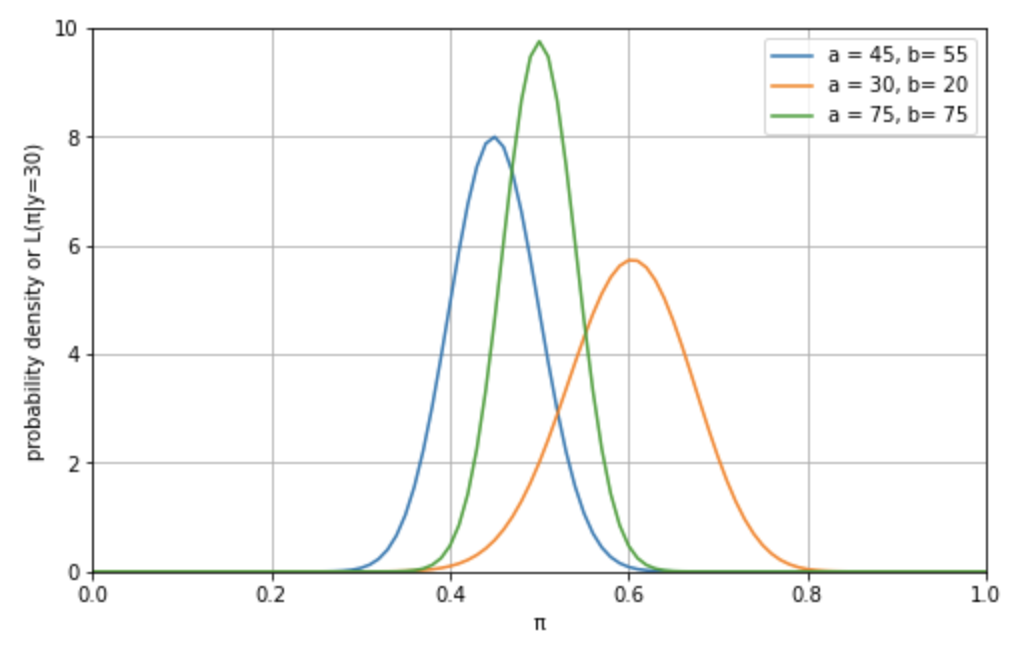
図 1.3.b. \(\pi\) の事前確率分布（青）と、\(\pi, y=30 of n=50\) の尤度関数（オレンジ）、\(\pi\) の事後確率分布（緑）

答えから言うと、この緑の事後確率分布の確率密度関数は以下の通りになります。

\[\begin{eqnarray}
\pi|(Y=30) \sim \rm{Beta}(75,75)
\end{eqnarray}\]

\[\begin{eqnarray}
f(\pi|y=30)
=
\dfrac{\Gamma(150)}{\Gamma(75)\Gamma(75)}
\pi^{74}(1-\pi)^{74} \ \ \ \rm{for} \ \in[0,1]
\end{eqnarray}\]

それでは、この事後確率分布の確率密度関数はどのように導き出されているのでしょうか。これは、ベイズの定理を使って、事前確率分布と尤度関数から求められます。

確率分布用のベイズの定理

今回求めたいのは、50 人中 30 人が Z 氏を支持すると答えた場合の支持率 \(\pi\) なので \(y=30\) となります。

\[
f(\pi|y=30)
=
\dfrac
{f(\pi)f(y=30|\pi)}
{f(y=30)}
\]

このうち分母の \(f(y=30)\) は定数なので、計算においては、上の式は \(f(\pi|y=30)
\propto f(\pi)L(\pi|y=30)\) とすることができます（\(\propto\) は「比例する」という意味の記号です）。そして、実際に求めると以下の通りになります。

\[\begin{eqnarray}
f(\pi|y=30)
&\propto&
f(\pi)L(\pi|y=30)\\
&=&
\overset{定数}
{\dfrac
{\Gamma(100)}
{\Gamma(45)\Gamma(55)}
\pi^{44}(1-\pi)^{54}}
\cdot
\overset{定数}
{\dbinom{50}{30}}\pi^{30}(1-\pi)^{20}\\
&=&
\overset{定数}{
\left[
\dfrac
{\Gamma(100)}
{\Gamma(45)\Gamma(55)}
\dbinom{50}{30}
\right]}
\cdot
\pi^{74}(1-\pi)^{74}\\
&\propto&
\pi^{74}(1-\pi)^{74}\\
\end{eqnarray}\]

ちなみに、正規化定数の部分を計算すると以下の通りになります。

\[\begin{eqnarray}
1
=
\int f(\pi|y=30)d\pi
=
\int c
\cdot
\pi^{74}(1-\pi)^{74}d\pi
\Rightarrow
c=
\dfrac
{1}
{\int \pi^{74}(1-\pi)^{74}d\pi}
\end{eqnarray}\]

ただし、繰り返しになりますが、これは計算する必要はありません。核（カーネル）となる、\(\pi^{74}(1-\pi)^{74}\) の部分が一致しているというところが重要です。定数部分がなくても、この核（カーネル）があれば、全ての分析が可能になるからです。

これが共役事前分布の利点です。共役事前分布でない場合は、いちいち分母の積分を行わなければ事後確率分布として分析可能な形にはならないようになっています。この理由から、ベイズ推定を行う際は、共役事前分布が使われます。

さらに共役事前分布の利点は、計算の際に積分をおこなわくて済むだけではありません。共役事前分布を使うと、事前確率分布と事後確率分布が同じ種類の確率分布になるため、分析が非常にやりやすくなるのです。

次にこの点についてみていきましょう。

\[\pi|y=30=\rm{Beta}(75,75)\]

\[
f(\pi|y=30)
\propto
\pi^{74}(1-\pi)^{74}
\]

2.1.4. 事後ベータ分布の分析

繰り返しになりますが、事前確率分布と尤度関数が共役関係の組み合わせであるベータ – 二項モデルでは、事後確率分布もベータ分布になります。そして、事前確率分布と事後確率分布がどちらも同じベータ分布であるということは、分析が非常にやりやすくなることを意味します。

以下の表をご覧ください。

これは、事前確率分布と事後確率分布の、期待値、最頻値、分散、標準偏差をそれぞれ計算したものです。どちらも同じベータ分布なので、こうした計算が全く同じ公式で行えます。なお公式は、『ベータ分布とは？誰でも必ず理解できるようにわかりやすく解説』で解説しています。

	α	β	期待値	最頻値	分散	標準偏差
事前モデル	45	55	0.45	0.449	0.002450	0.04950
事後モデル	75	75	0.50	0.500	0.001656	0.04069

これを見ると、まず Z 氏の支持率は、以前の 0.45 から 0.50 に上昇していることがわかります。

\[
E(\pi) = 0.45 \ \ \ \Rightarrow \ \ \ E(\pi|y=30) = 0.50
\]

さらに、標準偏差も小さくなっているので、確率分布の横の広がりが狭くなっていることがわかります。

\[
\rm{SD}(\pi) \approx 0.0495 \ \ \ \Rightarrow \ \ \rm{SD}(\pi|y=30) \approx 0.0407
\]

2.2. ガンマ−ポアソン分布共役族

事前ガンマ分布モデルのパラメータが形状母数 \(s\) と尺度母数 \(r\) で、データの尤度関数モデルのパラメータがポアソン分布の頻度パラメータ \(\lambda\) であるのとき、事後ガンマ分布モデルは以下の通りになります。

ガンマ−ポアソン共役族

\[\begin{eqnarray}
&{\small 事前}&: \sim \rm{Gamma}(s,r), \\
&{\small 尤度}&: \sim \rm{Pois}(\lambda), \\
&{\small 事後}&: \sim \rm{Gamma}(s+\Sigma y_i,r+n)
\end{eqnarray}\]

以下の問題を例に実際に見ていきましょう。

問題：詐欺電話

A さんは以前から、毎日数件かかってくる詐欺電話の多さに頭を悩ませていました。そこで、一日あたりにかかってくる詐欺電話の平均数を変数 \(\lambda\) として、モデル化することにしました。

\(\lambda\) : 一日あたりにかかってくる詐欺電話の平均回数

A さんは事前確率分布として、一日あたりの詐欺電話の平均回数は全体としては \(\lambda=5\) 回程度だろう、しかし少ないときは \(2\) から多いときは \(7\) ぐらいの上下の振れ幅があるだろうと考えました。

続いて、A さんは \(4\) 日間に渡って、詐欺電話の数をデータとして記録したところ、\(1\) 日目 \(6\) 件、\(2\) 日目 \(2\) 件、\(3\) 日目 \(2\) 件、\(4\) 日目 \(1\) 件の合計 \(11\) 件でした（*このデータは、確率変数 \(\lambda\) のポアソン分布に従います）。

この時、事後確率分布はどのようにモデル化できるでしょうか。

今まで解説してきた通り、ベイズ推定は以下の３つのステップで行います。

事前確率分布を求める
尤度関数を求める
事後確率を求める

早速見ていきましょう。

2.2.1. 事前ガンマ分布モデル

データ（尤度関数）がポアソン分布に従う場合、事前確率分布には、その共役事前分布であるガンマ分布を使うと計算が簡便になります。ガンマ分布については、『ガンマ分布とは？誰でも必ず理解できるようにわかりやすく解説』で詳しく解説しています。

\[\lambda \sim \rm{Gamma}(s,r)\]

確率密度関数は以下の通りです。

\[\begin{eqnarray}
f(\lambda)
=
\dfrac
{r^s}
{\Gamma(s)}
\lambda^{s-1}
e^{-r\lambda}
\ \ \ \ \rm{for} \ \lambda > 0
\end{eqnarray}\]

* \(\lambda\) : 確率変数,　\(s\) : 形状母数,　\(r\) : 尺度母数

ガンマ分布の分析指標は以下の公式で求めることができます。

\[\begin{eqnarray}
E(\lambda) &=& \dfrac{s}{r}\\
\rm{Mode}(\lambda) &=& \dfrac{s-1}{r} \ \ \ \rm{for} \ s \geq 1 \\
\rm{Var}(\lambda) &=& \dfrac{s}{r^2}
\end{eqnarray}\]

さて、A さんの予想は、一日あたりの詐欺電話の平均回数 \(\lambda\) は \(5\) 回であり、上下に \(2\) 回から \(7\) 回の幅があるだろうというものです。これをガンマ分布で表してみましょう。

まず、\(\lambda=5\) ということは、期待値が \(5\) ということですから、ガンマ分布の形状母数と尺度母数の関係は、次の通りになっているということになります。

\[
E(\lambda) = \dfrac{s}{r} \approx 5
\]

つまり \(s=5r\) であるということです。次に、\(\lambda\) の値は \(2\) から \(7\) の間に収まるようにしたいと考えています。この条件でいくつか入力してみると、\(\rm{Gamma}(10, 2)\) が事前モデルとして合うことがわかります。

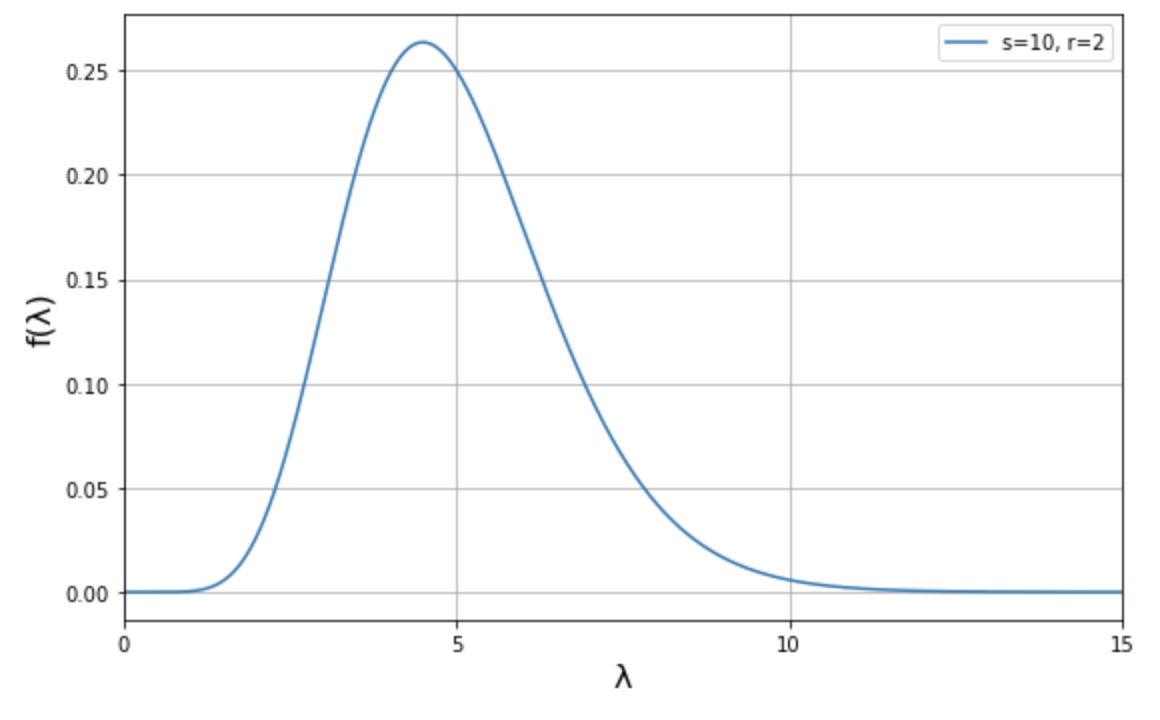
図 1.1. 一日あたりの詐欺電話の平均回数 \(\lambda\) に関する \(\rm{Gamma}(10, 2)\) の事前確率密度関数

これらの \(s\) と \(r\) の値を上述の確率密度関数に代入すると以下のようになります。

\[\begin{eqnarray}
f(\lambda)
=
\dfrac
{2^{10}}
{\Gamma(2)}
\lambda^{2-1}
e^{-10\lambda}
\ \ \ \ \rm{for} \ \lambda > 0
\end{eqnarray}\]

これが事前確率分布モデルです。

2.2.2. ポアソン尤度関数

続いて尤度関数を求めます。これは問題文で指定している通り、離散型確率分布のポアソン分布で定義します。ここで使う記号の意味はそれぞれ以下の通りです。

\(Y=11\)：4 日の間で詐欺電話がかかってくる数
\(y_1=6, \ y_2=2, \ y_3=2, \ y_4=1\)：1 日目、2 日目、3 日目、4 日目に電話がかかってくる数
\(\lambda\) ：一日あたりにかかってくる詐欺電話の割合（平均回数）

このとき、一日に平均 \(\lambda=5\) 回起こる事象が \(y_i\) 回起こることの尤もらしさは、ポアソン分布によって以下のようにモデル化することができます。

\[
y_i|\lambda \sim \rm{Pois}(\lambda)
\]

そしてポアソン分布モデルの確率密度関数は次の通りです。

\[\begin{eqnarray}
f(y_i|\lambda)
=
\dfrac{\lambda^{y_{i}}}{y_{i}!}e^{-\lambda} \ \ \rm{for} \ \ y \in \{0, 1, 2, \cdots\}
\end{eqnarray}\]

\(f(y_1=6|\lambda), \ f(y_2=2|\lambda), \ f(y_3=2|\lambda), \ f(y_4=1|\lambda))\) をそれぞれ計算してグラフ化すると以下のようになります。

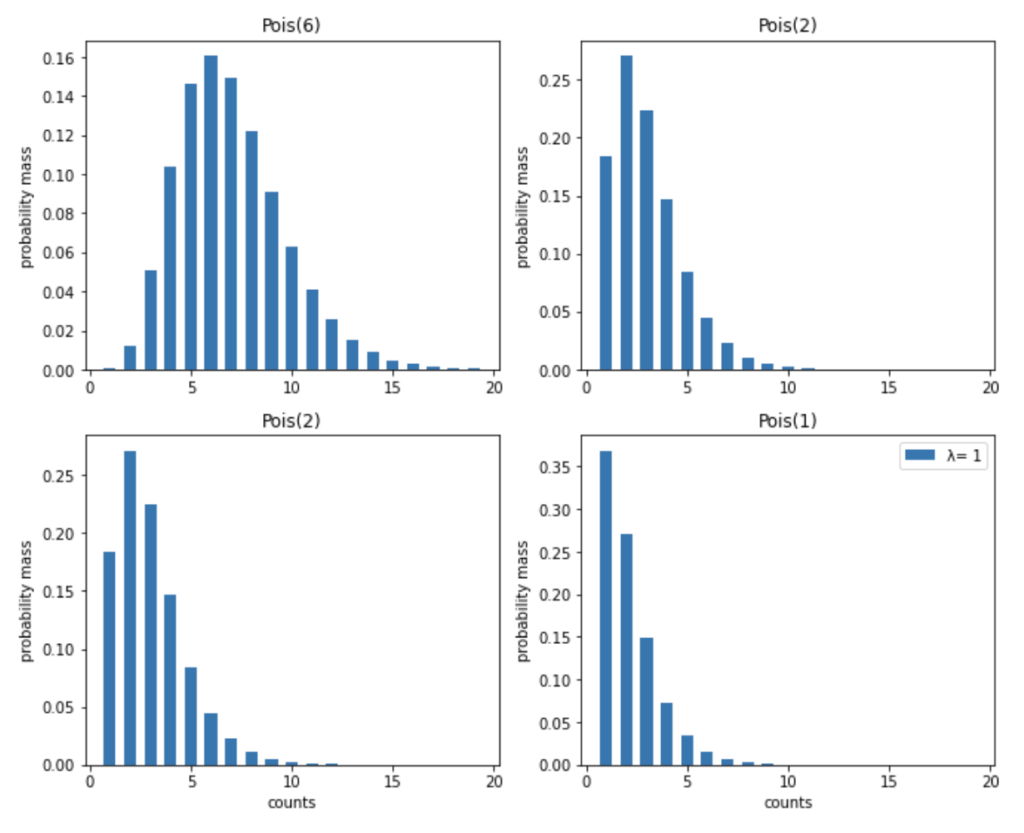
図 1.2.a. 異なる \(\lambda\) におけるポアソン分布の確率質量関数

さて、事後確率を求める上では、基本的には、この 4 つの尤度関数を 1 つずつ事前確率と組み合わせていけば良いのですが、それは面倒です。そこで、これら 4 つの尤度関数を 1 つにまとめることにします。

そのためには同時確率質量関数 “Joint probability mass function ” というものを使います。同時確率質量関数は考え方としては、独立事象の積と同じです。

\[
P(A \cap B \cap C \cap D)=P(A) \cdot P(B) \cdot P(C) \cdot P(D)
\]

これの \(P(A) \cdot P(B) \cdot P(C) \cdot P(D)\) が、それぞれの尤度関数の積 \(f(Y_{1}| \lambda)
\cdot f(Y_{2}| \lambda) \cdot f(Y_{3}| \lambda) \cdot f(Y_{4}| \lambda)\) になっただけです。

これを計算すると以下の通りの同時確率質量関数になります。

\[\begin{eqnarray}
f(Y| \lambda)
&=&
\prod_{i=1}^n
f(y_{i}| \lambda)\\
&=&
f(y_{1}| \lambda)
\cdot
f(y_{2}| \lambda)
\cdot
f(y_{3}| \lambda)
\cdot
f(Y_{4}| \lambda)\\
&=&
\dfrac{\lambda^{y_{1}}}{y_{1}!}e^{-\lambda}
\cdot
\dfrac{\lambda^{y_{2}}}{y_{2}!}e^{-\lambda}
\cdot
\dfrac{\lambda^{y_{3}}}{y_{3}!}e^{-\lambda}
\cdot
\dfrac{\lambda^{y_{4}}}{y_{4}!}e^{-\lambda}\\
&=&
\dfrac
{
\lambda^{\Sigma y_i} e^{-n\lambda}
}
{
\prod_{i=1}^n y_i!
}
\end{eqnarray}\]

* \(n\) は \(y_n\) の \(n\)

これの最後の行は、以下の性質から導き出したものです。

\[\begin{eqnarray}
x^ax^b=x^{a+b} \ \ \rm{and} \ \ x^ay^a=(xy)^a
\end{eqnarray}\]

さて、分母の総積の部分は定数であるため、尤度関数は以下の通りになります。

\[\begin{eqnarray}
f(Y| \lambda)
\ \propto \
\lambda^{\Sigma y_i} e^{-n\lambda}
\ \ \ \ \ \rm{for} \ \lambda >0
\end{eqnarray}\]

以上が尤度関数（4 つの尤度関数を 1 つにした同時確率質量関数）です。これに実際のデータを埋め込むと、以下の通りになります。

\[\begin{eqnarray}
f(Y| \lambda)
\ \propto \
\lambda^{11} e^{-4\lambda}
\end{eqnarray}\]

これをグラフにしたものが以下です。

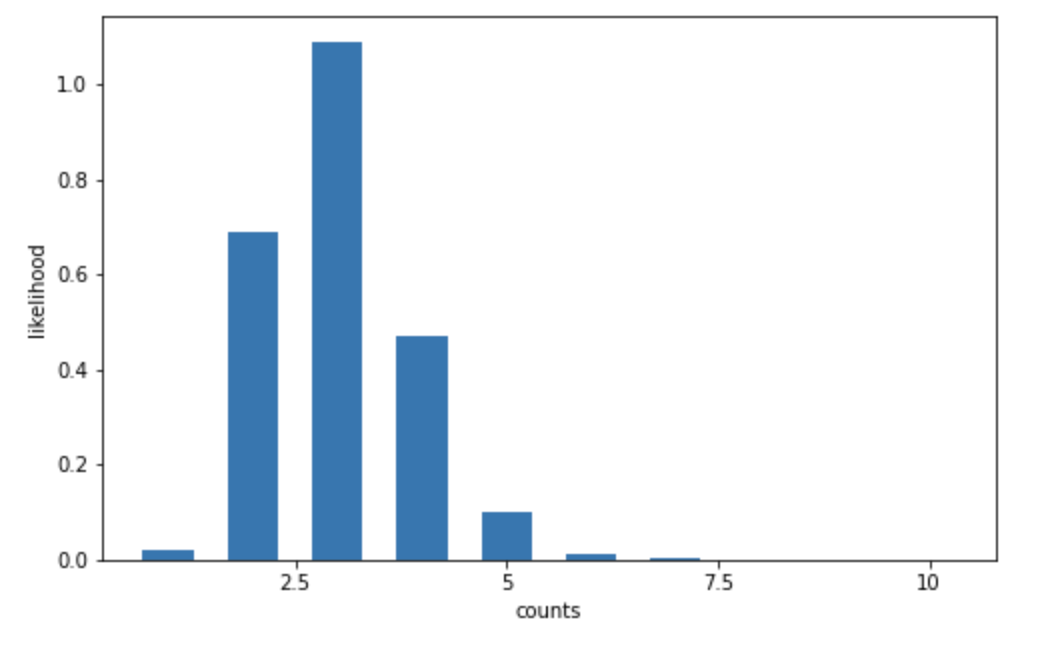
図 1.2.b. 4 日間の実際の詐欺電話の数が与えられている場合の、一日あたりの詐欺電話の平均回数 \(\lambda\) の尤度関数

2.2.3. 事後ガンマ分布モデル

これで事前確率分布がガンマ分布、尤度関数がポアソン分布という共役の組み合わせになりました。

\[\begin{eqnarray}
Y|\lambda &\sim& \rm{Pois}(\lambda)\\
\lambda &\sim& \rm{Gamma}(s,r)
\end{eqnarray}\]

そして、この共役族の場合、事後分布は以下のように形状母数と尺度母数がそれぞれ更新された新しいガンマ分布になります。

\[\begin{eqnarray}
\lambda|Y
\sim
\rm{Gamma}(s+\Sigma y_i,r+n)
\end{eqnarray}\]

* \(n\) は \(y_n\) の \(n\)

実際に計算して証明してみましょう。

\[\begin{eqnarray}
f(\lambda|Y) \propto f(\lambda)f(Y|\lambda)
&=&
\dfrac
{r^s}
{\Gamma(s)}
\lambda^{s-1}
e^{-r\lambda}
\cdot
\dfrac
{
\lambda^{\Sigma y_i} e^{-n\lambda}
}
{
\prod_{i=1}^n y_i!
}\\
&\propto&
c \cdot \lambda^{s-1} e^{-r\lambda}
\cdot \lambda^{\Sigma y_i} e^{-n\lambda}\\
&=&
\lambda^{s+\Sigma y_i-1}
e^{-(r+n)\lambda}
\end{eqnarray}\]

こうして最後に残ったのは、事後確率密度関数のカーネルです。そして、このカーネルは形状母数が \(s+\Sigma y_i-1\)、尺度母数が \(r+n\) のガンマ分布の確率密度関数に相当しています。このことから、あらためて以下の公式が証明されます。

\[\begin{eqnarray}
\lambda|Y
\sim
\rm{Gamma}(s+\Sigma y_i,r+n)
\end{eqnarray}\]

* \(n\) は \(y_n\) の \(n\)

これを A さんの詐欺電話の問題に適用しましょう。

事前確率分布が \(f(\lambda) = \rm{Gamma}(10, 2)\) で、尤度関数が \(f(Y\lambda)=\lambda^{11} e^{-4\lambda}\) なので、次の通りになります。

\[\begin{eqnarray}
f(\lambda|Y)
=
\rm{Gamma}(10+11,2+4)
=
\rm{Gamma}(21,6)
\end{eqnarray}\]

* \(n\) は \(y_n\) の \(n\)

これをグラフにすると下図の通りに、事後確率モデルがわかります。

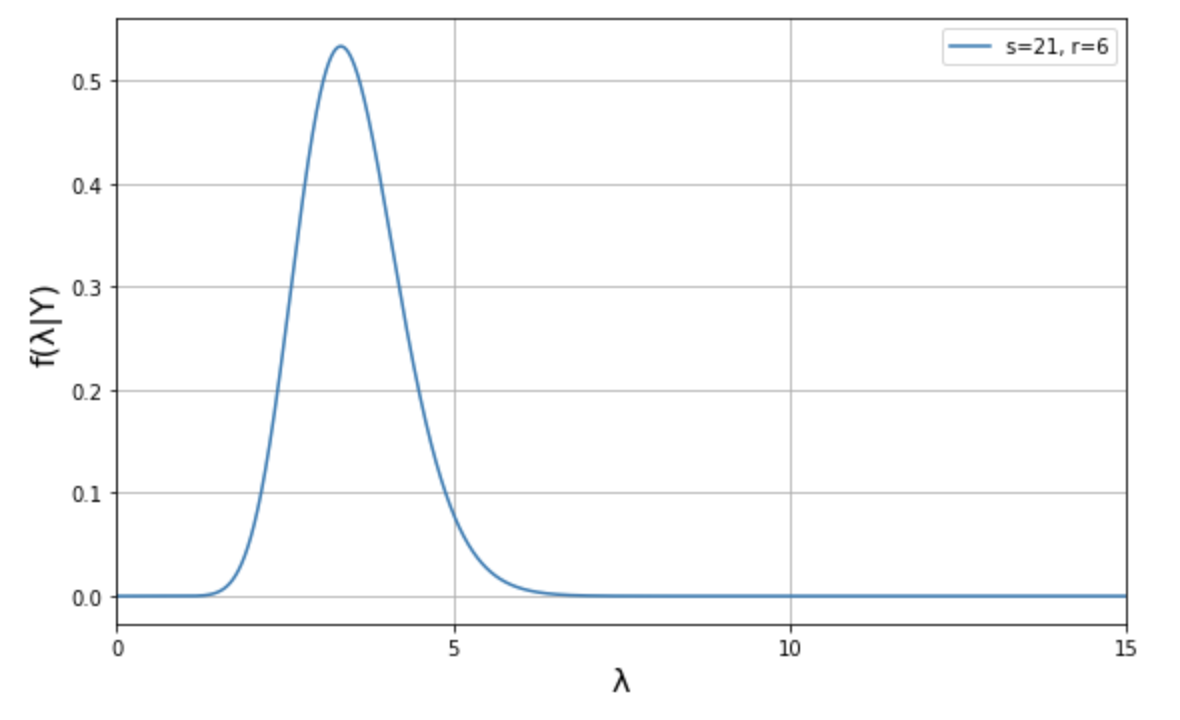
それぞれ見比べてみると、事前確率分布が以下のように変化していることがわかります。

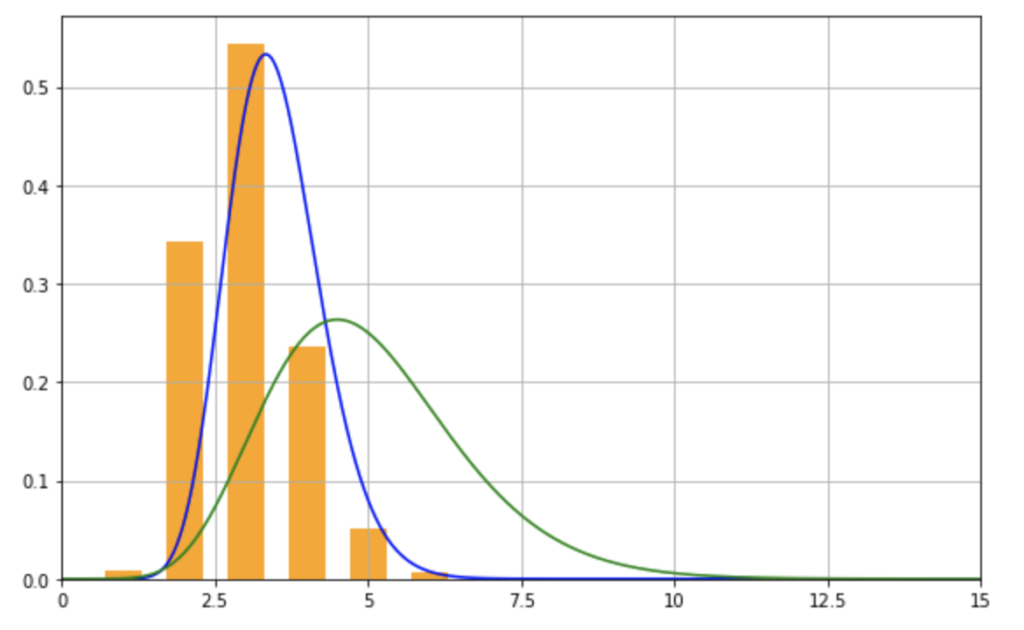
それぞれ指標を比較してみましょう(計算式は省きます)。

	s	r	mean	mode	var	sd
事前モデル	10	2	5.0	4.50	2.50	1.58
事後モデル	21	6	3.5	3.33	0.58	0.76

こうやって事前モデルと事後モデルを比較すると、さまざまなことがわかります。

2.3. 正規−正規分布共役族

ここまででベータ−二項共役と、ガンマ−ポアソン共役を見てきました。しかし、共役族はまだまだたくさんあって、全てをカバーするのは不可能です。しかし、もう一つだけ、知っておくと非常に便利な共役族があります。それが正規分布−正規分布共役族です。

正規分布−正規分布共役族では、事前の正規分布モデルのパラメータが平均値 \(\theta\)、標準偏差 \(\gamma\) で、データの尤度関数モデルのパラメータが平均値 \(\mu\)、標準偏差 \(\sigma\) のとき、事後の正規分布モデルは以下の通りになります。

正規分布−正規分布共役族

\[\begin{eqnarray}
&{\small 事前}&: \sim N(\theta, \gamma^2), \\
&{\small 尤度}&: \sim N(\mu, \sigma^2), \\
&{\small 事後}&:
\sim
N
\left(
\theta
\dfrac{\gamma^2}{n\gamma^2+\sigma^2}
+
\mu
\dfrac{n\gamma^2}{n\gamma^2+\sigma^2}
, \ \
\dfrac{\gamma^2 \sigma^2}{n\gamma^2+\sigma^2}
\right)
\end{eqnarray}\]

次の問題を実際に解いていくことで、この正規分布-正規分布共役族についての理解を深めていきましょう。

問題：脳震盪と海馬の体積

近年、サッカーやボクシングなどの頭部に衝撃を受ける可能性のあるスポーツについて、脳震盪のリスクが大きな注目を浴びるようになりました。

その中で調査の一環として、科学者たちは脳の中の海馬の体積に注目しました。脳震盪の病歴のある人は、海馬の体積が小さくなり、さまざまなリスクに晒されると考えたのです。

そこで脳震盪の病歴のある被験者25名の海馬の体積を調べたところ、以下の通りでした^{（Lock et al. 2016）}。

平均体積：5.735㎤
範囲：4.5 ~ 7 ㎤

以上のデータから事後確率を求めてみましょう。

2.3.1. 事前正規分布モデル

いつもの通り、ベイズ推定は事前確率分布モデルを構築するところから始まります。さて、今回は事前モデルとして、どの確率分布を使うのが適しているでしょうか。

まず、海馬の体積 \(X_i\) は連続値であることから、連続確率分布であるベータ分布、指数分布、ガンマ分布、正規分布、そして F 分布などが考えられます。この中でベータ分布は \(X_i \in[0,1]\) なので排除できます。残った中では、正規分布が最も適しています。なぜなら、生物学的なデータは大体、正規分布と一致するからです。

正規分布とは

まずは正規分布について簡単に解説しておきます。

正規分布モデルは確率変数 \(X\) は \(-\infty\) から \(\infty\) までの連続値です。このときの \(X\) の変動の具合は、平均値パラメータ \(\mu \in (-\infty, \infty)\) と標準偏差パラメータ \(\sigma>0\) で表されます。

\[
x
\sim
N(\mu, \sigma^2)
\]

正規分布の確率密度関数は以下の通りです。

\[\begin{eqnarray}
f(x)
=
\dfrac{1}{\sqrt{2\pi\sigma^2}}
\rm{exp}
\left[
–
\dfrac{(x-\mu)^2}{2\sigma^2}
\right]
\end{eqnarray}\]

そして、分析指標は以下の通りです。

平均値 \(E(x)=\rm{Mode}(x)=\mu\)
分散 \(\rm{Var}(x)=\sigma^2\)
標準偏差 \(\rm{SD}(x)=\sigma\)

そして正規分布の最大の性質の一つに、データの95%が以下の範囲に収まるというものがあります。

\[\mu ± 2 \sigma\]

以下のグラフは、様々な平均値 \(\mu\) と標準偏差 \(\sigma\) の場合の正規分布を表しています。

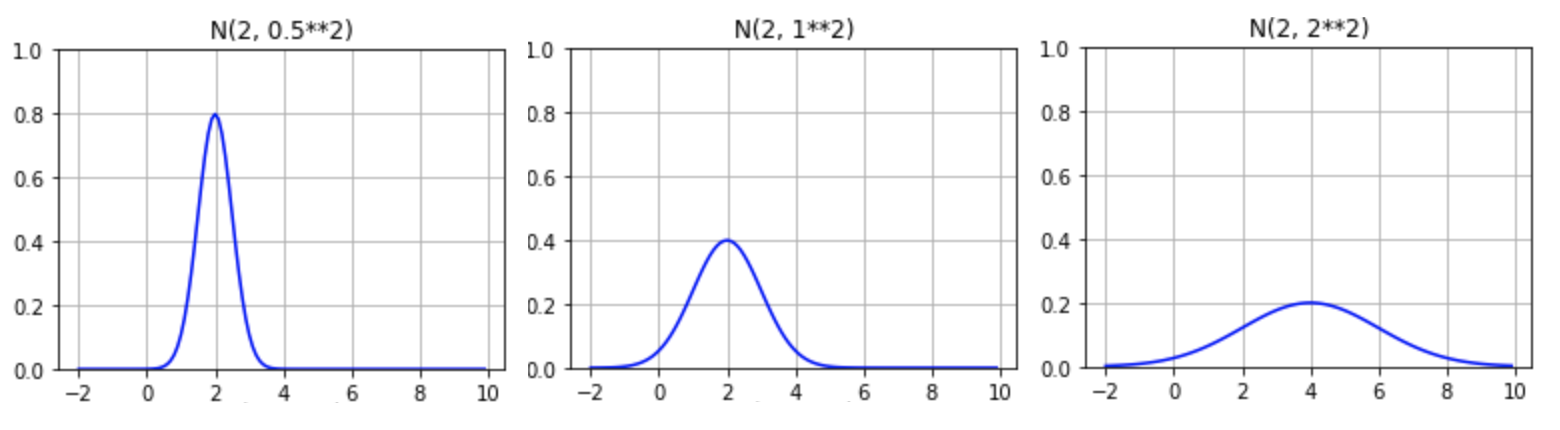
図 3.1.1. 異なる平均値 \(\mu\) と標準偏差 \(\sigma\) の場合の正規分布の確率密度関数

ご覧のように、正規分布は常に釣鐘の形状をしており、平均値 \(\mu\) を中心として左右対称になります。そのため、\(\mu\) が大きくなるほどカーブは右側にシフトし、\(\sigma\) が大きくなるほど裾の広がりが大きくなります。そして、常にデータの 95% は、\(\mu ± 2 \sigma\) の範囲に収まり、\(\mu ± 3 \sigma\) 以上の部分は無視して構わないほどのパーセンテージになります。

事前確率分布を正規分布で表す

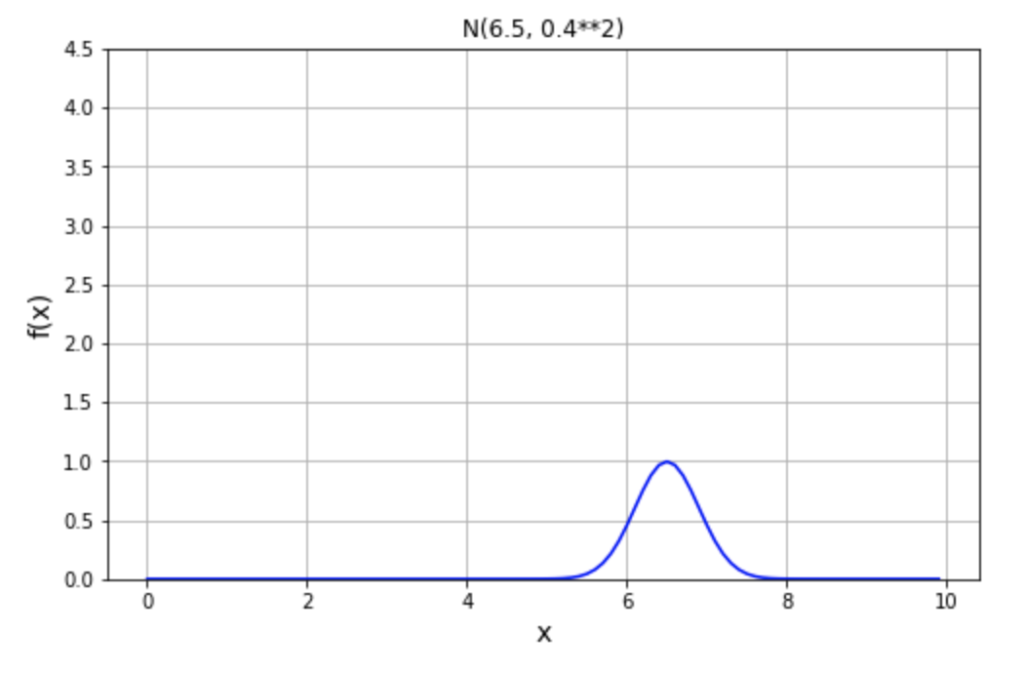
それでは正規分布を使って、脳震盪の病歴のある人の海馬の体積についての事前確率分布モデルを構築しましょう。

ここでは事前情報として wikipedia の海馬に関するページを参照することにします。ここには、海馬の平均体積は、一方の脳で 3.0 ~ 3.5 ㎤であると書かれています。左右の脳を合わせると体積の範囲は 6.0 ~ 7.0 ㎤になり、平均値は 6.5 ㎤あたりだろうと予測することができます。

これは以下の通り、平均値 \(\theta=6.5\)、標準偏差 \(\gamma=0.4\) の事前正規分布モデルで表すことにします。

\[\begin{eqnarray}
f(x)
=
\dfrac{1}{\sqrt{2\pi\cdot0.4^2}}
\rm{exp}
\left[
–
\dfrac{(x-6.5)^2}{2\cdot0.4^2}
\right]
\propto
\rm{exp}
\left[
–
\dfrac{(x-6.5)^2}{2\cdot0.4^2}
\right]
\end{eqnarray}\]

図 3.1.2. 平均値 \(\mu=6.5\) と標準偏差 \(\sigma=0.4\) の正規事前確率分布モデル

2.3.2. 正規尤度関数モデル

Lock et al. 2016 の調査では、脳震盪の病歴のある25 名の人々の海馬の平均体積は \(\overline{x}=5.735\) ㎤で、その範囲は \(4.5 \sim 7\) ㎤でした。これは、平均値 \(\mu=5.735\)、標準偏差 \(\sigma=0.5\) の正規分布で表すことにします。

\[\begin{eqnarray}
f(d|x)
=
\dfrac{1}{\sqrt{2\pi\cdot0.5^2}}
\rm{exp}
\left[
–
\dfrac{(x-5.735)^2}{2\cdot0.5^2}
\right]
\propto
\rm{exp}
\left[
–
\dfrac{(x-5.735)^2}{2\cdot0.5^2}
\right]
\end{eqnarray}\]

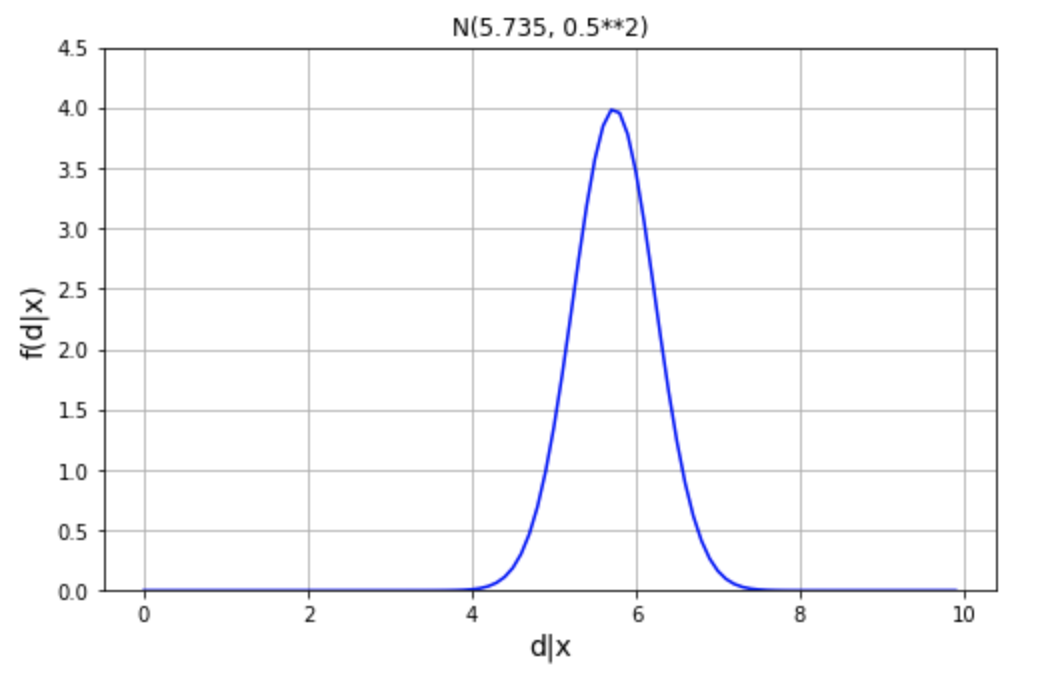
図 3.2. 平均値 \(\mu=5.735\) と標準偏差 \(\sigma=0.5\) の正規事前確率分布モデル

以上が尤度関数モデルです。

2.3.3. 事後正規分布モデル

これで事前モデルと尤度関数が揃いました。

\(\theta=6.5, \gamma=0.4\)
\(\mu=5.735, \sigma=0.5\)

あとは正規−正規分布共役族の公式の通りに計算することで、事後モデルを求めることができます。

\[\begin{eqnarray}
f(x|d)
&=&
N
\left(
\theta
\dfrac{\gamma^2}{n\gamma^2+\sigma^2}
+
\mu
\dfrac{n\gamma^2}{n\gamma^2+\sigma^2}
, \ \
\dfrac{\gamma^2 \sigma^2}{n\gamma^2+\sigma^2}
\right)\\
&=&
N
\left(
6.5 \cdot
\dfrac{0.5^2}{25\cdot 0.4^2+0.5^2}
+
5.735 \cdot
\dfrac{25\cdot0.4^2}{25 \cdot 0.4^2+0.5^2}
, \ \
\dfrac{0.4^2 \cdot 0.5^2}{25 \cdot 0.4^2+0.5^2}
\right)\\
&=&
N(5.78, 0.0094)
\end{eqnarray}\]

それぞれをグラフにして比較すると下図の通りになります。

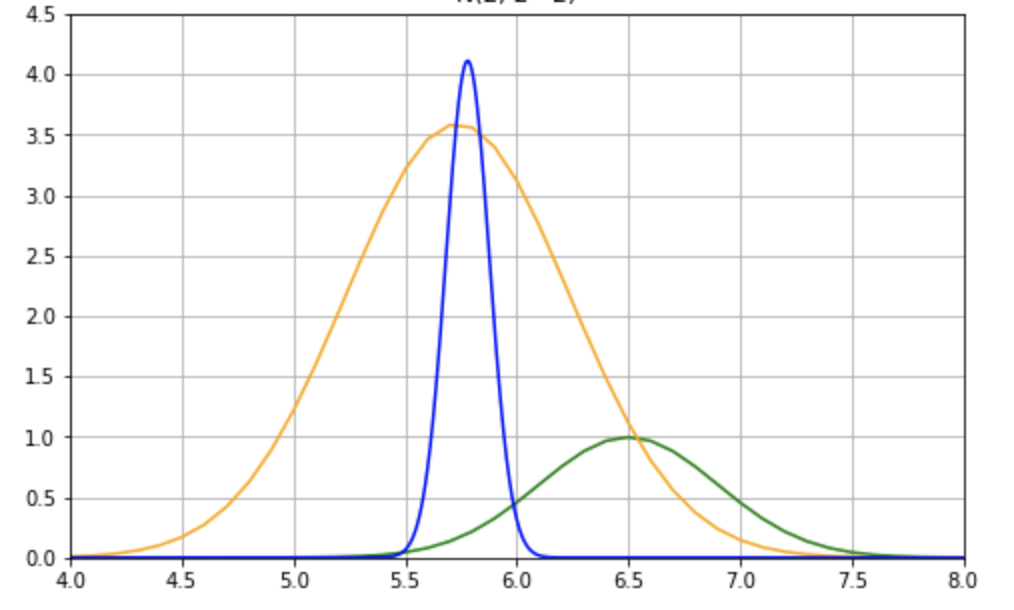
これを見ると、脳震盪の病歴がある場合は、海馬の体積は小さくなっていることがわかります。参考に事前モデルと事後モデルの分析指標を下表に記しておきます。

	mean	mode	var	sd
事前モデル	6.50	6.50	0.16	0.40
事後モデル	5.78	5.78	0.0094	0.097

3. 共役事前分布のデメリット 2 つ

ここまで見てきたように共役事前分布を使えば、ベイズ推定の計算が非常に簡単になり、事前モデルと事後モデルの比較も簡単になります。しかし、共役事前分布にもデメリットはあります。それが以下の 2 つです。

1 つ目は、事前分布モデルは、事前情報に常に完璧に適合するわけではないということです。例えば、正規分布のモデルは、常に平均値 \(\mu\) を境に左右対称です。そのため、事前理解が左右対称でない場合は、正規分布がベストなチョイスということにはなりません。共役事前分布を使うということは、このような多少の誤差を踏まえた上で、あえて正規分布を選ぶということです。

2 つ目は共役族では完全にフラットな事前モデルを描くのが不可能な場合があるということです。このような事前モデルはベータ分布で、\(\alpha=1, \beta=1\) で実現することは可能です。しかし、正規分布やガンマ分布など、範囲が無限の分布では、フラットな事前モデルを描くことはできません。ただし、分散を非常に大きくとって、ほとんどフラットな事前モデルを描くことは可能です。

ただし、これら 2 つのデメリットは、データが十分に大きい場合は無視して良いほど小さくなります。そのため結論から言って、このようなデメリットは大きな問題にはなりません。従って、共役事前分布は非常に優れていると言えます。