ベイズの定理は、簡潔に述べると「事前確率(もともと持っている信念や考え)が尤度(新しいデータや経験)を受けて、どう変化するのかを示す事後確率を求めるための方法」です。
ベイズの定理は今では、統計学の主流であり、人工知能やディープ・ラーニングといった最先端の分野の中核となっているベイズ統計を理解する上で、土台となる概念です。そこで、このページでは、このベイズの定理について理解しておきたいことを全て、余すところなく、わかりやすく解説していきます。
具体的には、あなたは以下の事柄を吸収することができます。
- ベイズの定理とは何かを、用語の正しい意味や記号の正しい書き方を含めて理解できる:ベイズの定理とは要するにどういうものなのか、その本質がわかります。そして、事前確率・尤度・周辺尤度・事後確率といった用語の正しい意味や、それぞれの正しい表記方法が身に付きます。
- 例題を通してベイズの定理の理解を深められる:例題を通して、ベイズの定理の計算方法、そして、事前確率・尤度・周辺尤度・事後確率のそれぞれの意味が直感的に理解できるようになります。
- 実際にベイズの定理を用いて練習問題を解く:あたな自身で、事前確率とデータモデル(尤度)、周辺尤度を求め、ベイズの定理を使って、そこから事後確率を導き出すことを行なってもらいます。練習問題は 3 つあります。すべてがベイズの定理に対して、異なる気づきを与えてくれる問題になっています。
- 実用上、役立つベイズの定理の性質がわかる:本文中で詳しく解説していますが、ベイズの定理とは、「信念が経験やデータによって変化することを数式化したもの」です。そして、どのような場合に信念がデータに影響されて、どのような場合に影響されないのかという重要な性質を紹介します。
- ベイズ更新の実用方法がわかる:ベイズ更新は、ベイズの定理の二つ目の本質であり、「新しいデータや経験を取得するたびに、事後確率を洗練させていくプロセス」のことです。このベイズ更新について、実際に問題を解きながら、どういうものなのかをハッキリと理解することができます。
それでは見ていきましょう。
1. ベイズの定理とは
ここでは、まずベイズの定理について最も基本的な知識である以下の 2 点を解説します。
- ベイズの定理の公式
- ベイズの定理の 2 つの本質
これらは数式的にも、概念的にも、ベイズの定理を使いこなせるようになる上での土台となりますので、ぜひ、ここでしっかりと抑えておきましょう。
1.1. ベイズの定理の公式
ベイズの定理とは以下の公式のことです。
ベイズの定理
\[\begin{eqnarray}
P(H|D)
=
\dfrac
{P(H)P(D|H)}
{P(D)}
\end{eqnarray}\]
\(H\):仮説 \(D\):データ
ベイズの定理は、公式としては、条件付き確率を変形したものに過ぎません。しかし、それだけなのにも関わらず、公式が持つ意味合いは、以下のように大きく変化します。
\[\begin{eqnarray}
\overbrace{
\overset{\small B後のAの確率}{P(A|B)}=
\dfrac
{
\overset{\small Aの確率}{P(A)}
\cdot
\overset{\small A後のBの確率}{P(B|A)}
}
{
\underset{\small Bの確率}{P(B)}
}
}^{条件付き確率}
\ \ \
\Leftrightarrow
\ \ \
\overbrace{
\overset{\small 事後確率 }{P(H|D)}
=
\dfrac
{\overset{\small 事前確率 \ }{P(H)}
\cdot
\overset{\small 尤度}{P(D|H)}}
{
\underset{周辺尤度}{P(D)}
}
}^{ベイズの定理}
\end{eqnarray}\]
- 事前確率 \(P(H)\):事前にデータ D が何もない状態で、仮説 H が正しい確率
- 尤度 \(P(D|H)\):仮説 H が正しいとした時の、データ D の尤もらしさ
- 周辺尤度 \(P(D)\):仮説 H の真偽を問わず、データ D を観察する可能性
- 事後確率 \(P(H|D)\):データ D を踏まえて、仮説 H が正しい確率
ベイズの定理の最大の功績は、このように、それぞれのパーツの意味合いを具体的にしたことにあります。
なぜならこのように意味づけが与えられることで、単なる条件付き確率が、「人がもともと持っている信念や常識(事前確率)が、新しい経験やデータ(尤度)に触れた時に、どのように変化するべきか(事後確率)」という、知識が発展するプロセスを説明する公式へと昇華されたからです。
これこそがベイズの定理が AI 分野において必要不可欠である最大の理由です。
それでは、それぞれの用語を一つずつ解説しながら、ベイズの定理について理解していきましょう。
1.1.1. 事前確率とは
まず事前確率 \(P(H)\) とは、「私たちが持っている仮説(=信念)が真である確率』です。
たとえば、SNS上にはフェイクニュースが溢れています。そして、ある研究によるとニュース \(100\) 記事あたりの \(40 \%\) がフェイクニュースであったようです(Shu et al. 2017)。
この研究から、私たちは「SNS上のニュース記事のうち \(40 \%\) はフェイクニュースである」という仮説(=信念)を持つことができます。この \(40 \%\) という数字が事前確率であり、\(P(H)=0.4\) と表します。
なお事前確率 \(P(H)\) を視覚的に表すと下図のようになります。

1.1.2. 尤度とは
続いて尤度について見ていきましょう。尤度 \(P(D|H)\) とは、「仮説(=信念)が真であるときに、データ \(D\) を観察する可能性(尤もらしさ)」です。
たとえば、「フェイクニュースでは、 \(30 \%\) の割合でタイトルに “!” が使われている」とします。見ての通り、これは仮説が正しい場合に、 ” ! ” が使われている可能性なので尤度であり、\(P(D|H)=0.3\) となります。
一方で、「フェイクニュースでない場合は、\(10 \%\) の割合でタイトルに “!” が使われている」可能性は、\(P(D|¬H)=0.1\) とします。
なお、尤度は確率と同じように \(\%\) で表すことができますが、厳密には確率ではないので、その合計は必ず \(1\) でなければいけないということはありません。
このデータこそが尤度です。そして、これを視覚的に表すと、下図の青文字の部分を意味します。
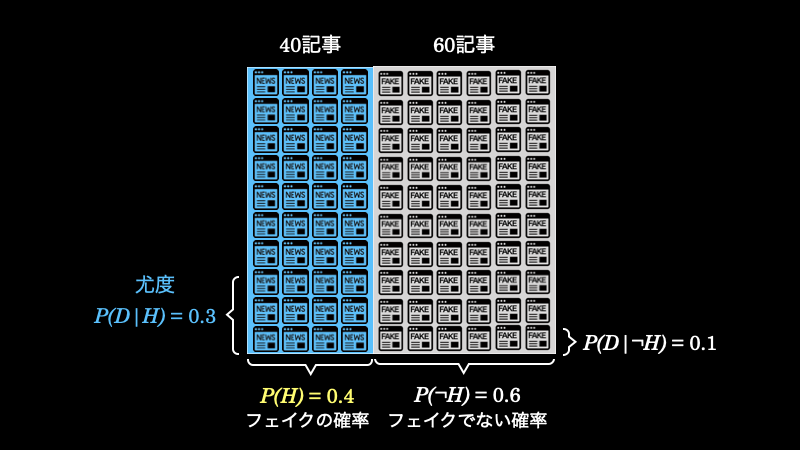
以上のことから、フェイクニュースが \(40\) 記事あったとしたら、その中で \(12\) 記事のタイトルに “!” が使われているということがわかります。これを表したのが、以下の緑の部分の面積(事前確率 \(P(H) \times\) 尤度 \(P(D|H)\))です。
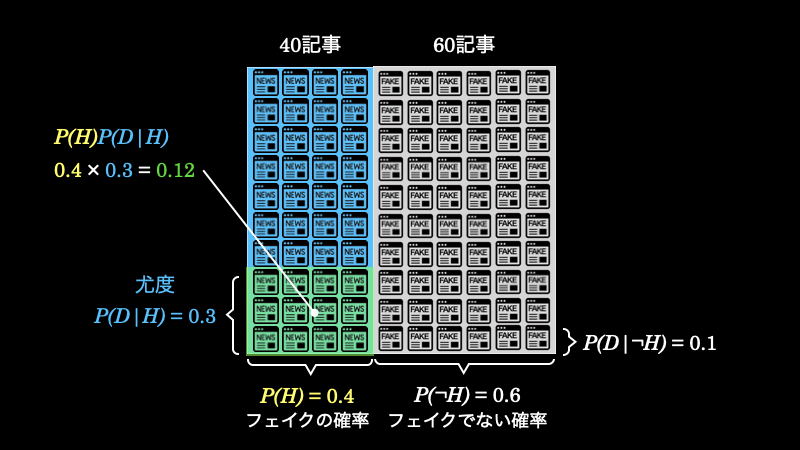
1.1.3. 周辺尤度とは
周辺尤度 \(P(D)\) とは、「データそのものを観察することの尤もらしさ」のことです。\(D\) はタイトルに “!” が使われている記事の割合です。
先ほど、フェイクニュースの中でタイトルに “!” が使われている記事の数が \(12\) 記事であることを求めました。しかし、フェイクではないニュースの中にも “!” が使われているものがあります。それを計算すると、下図の黄色い面積になり、\(6\) 記事であることがわかります。
周辺尤度はタイトルに “!” が使われているニュースの割合ですから、緑の面積が \(0.12=12\) 記事で黄色の面積が \(0.06=6\) 記事で合計 \(18\) 記事であるということになります。
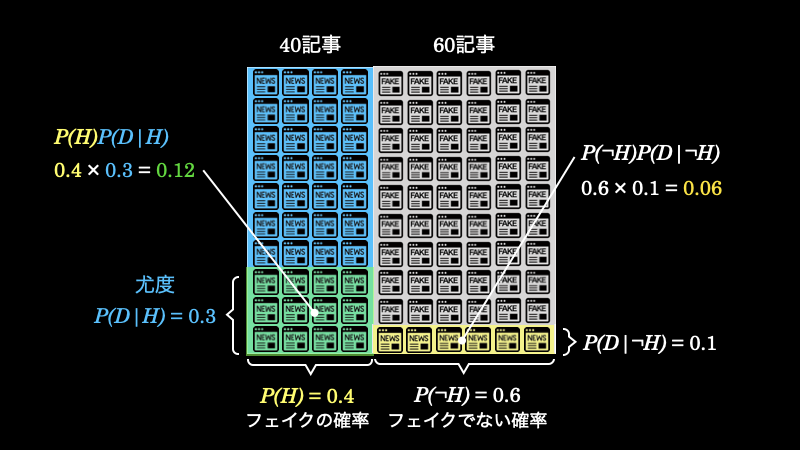
1.1.4. 事後確率とは
最後に事後確率 \(P(H|D)\) は、「データを観察した場合に、仮説が真である確率」です。
今回の場合は、タイトルに “!” が使われているニュースを見た場合に、それがフェイクニュースである確率のことです。
これは今まで求めてきた、事前確率 \(P(H)\)、尤度 \(P(D|H)\)、周辺尤度 \(P(D)\) を使って、ベイズの定理によって、次のように求めることができます。
\[\begin{eqnarray}
P(H|D)
&=&
\dfrac
{P(H)P(D|H)}
{P(D)}\\
&=&
\dfrac
{0.4\cdot 0.3}
{0.4\cdot 0.3 + 0.6\cdot 0.1}
=
\dfrac
{2}{3}
\end{eqnarray}\]
これは視覚的には下図の計算を意味しています。
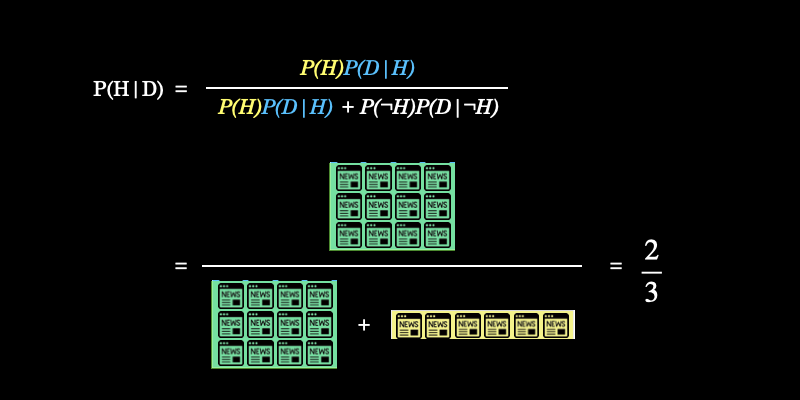
このように事後確率を求めることで、今後、SNS上でタイトルに “!” が使われているニュースを見たときは \(2/3\) の確率でフェイクニュースだから、読み飛ばそうと判断することが可能になるというわけです。
私たちは、もともと事前確率として、SNS上のニュースは、\(40 \%\) がフェイクニュースだと考えていました。ここに、フェイクニュースとフェイクではないニュースのタイトルに “!” が使われている割合というデータを加えれば、私たちはさらに高い確率で、SNS上のニュースがフェイクニュースであるかどうか判断できるようになるのです。
これがベイズの定理であり、事後確率です。
なお、事前確率、尤度、周辺尤度、事後確率を計算するときは、ぜひ、ここまで使ってきた画像のように視覚的に考えるようにしてください。そうすれば、ベイズの定理を自由自在に使いこなせるようになっていきます。
1.2. ベイズの定理の本質
ここまでだけでもベイズの定理が凄いものであることは何となく感じて頂けると思います。これについて、あらためて具体的に言及しておきましょう。
1.2.1. ベイズの定理は知識のアップデート
要するにベイズの定理の本質は、「事前知識は、新しいデータを吸収することによって、さらに優れた事後知識へと変わる」という点にあります。これを数字で簡単に計算できるようになったものがベイズの定理です。
上の例では、事前知識をアップデートすることによって、SNS上のフェイクニュースを見破る確率を \(40\%\) から \(67\%\) にまで引き上げることができました。
これが知識をアップデートするということの意味であり利点です。
1.2.2. ベイズ更新(知識は繰り返しアップデートできる)
ベイズの定理のもう一つの本質は、事前知識のアップデートは繰り返し行うことができるという点にあります。
いま、私たちは \(67\%\) の確率で、SNS上のフェイクニュースを見抜けるようになりました。そして、また新しいデータが収集できた時は、今度は、この数字を事前確率として扱って再計算することで、知識を再アップデートすることができるのです。
こうやって知識をアップデートすることで、精度をどんどん向上させていくことができるのです。これを数学的に実現できるというのが、ベイズの定理の凄さです。
そして、この方法のことを「ベイズ更新」と言います。これについては、後ほど、あらためて詳しく解説します。
2. ベイズの定理を例題で解説
しつこいかもしれませんが、ここでは上と同じようなフェイクニュースの問題を、例題形式で数値を変えてもう一度解説することにします。目的は理解をさらに強固なものにすることです。そして、そのためには反復練習が最適なのです。
というわけで、もう一度、上と似たような問題を用意したので、ぜひご自身で解いてみてから解説を読み進めてください。
それでは早速、以下の問題をご覧ください。
問題:フェイクニュースの確率
2017 年は流行語大賞のトップテンにフェイクニュースがランクインした年でした。この年、BuzzFeed の記者 5 名が、SNS に投稿された 150 のニュース記事を調べたところ、そのうち 40% (60/150) がフェイクだったようです(Shu et al. 2017)。
さらに、この 5 名の記者は、フェイクニュースに見られるいくつかの特徴を見つけ出しました。そのうちの一つが、記事タイトルでのエクスクラメーションマーク(!)の使用です。フェイクニュースの 26.67% (16/60) でエクスクラメーションが使われていました。一方で、リアルニュースでは、その割合はたったの 2.22% (2/90) でした。
| !有り | !なし | 合計 | |
| フェイクである | 16 | 44 | 60 |
| フェイクではない | 2 | 88 | 90 |
| 合計 | 18 | 132 | 150 |
今、あなたは SNS で新しいニュース記事をチェックするところです。そして、その記事のタイトルを見るとエクスクラメーションが使われています。この記事はフェイクニュースでしょうか。それともリアルニュースでしょうか。
ヒント:この問題において、仮説 \(H\) =フェイクニュースである、データ \(D\) =記事タイトルに!が付いている、です。
一見すると、どこから手をつけて良いのかわからず、とても難しく思えてしまいます。しかし、このような問題は「ベイズの定理」を使うことで、簡単に答えがわかるようになります。
というわけで、ベイズの定理を使って、この問題を解いていきましょう。なお、ベイズの定理のコツは、以下の 4 つのステップで解き進めることです。
- 事前確率 \(P(H)\) を求める
- 尤度 \(P(D|H)\) を求める
- 周辺尤度 \(P(D)\) を求める
- 事後確率 \(P(H|D)\) を求める
それでは見ていきましょう。
2.1. 事前確率を求める
まずは事前確率(事前データ D が何もない状態で、仮説 H が正しい確率)を求めます。
この問題では、事前確率 \(P(H)\) は、「事前情報が何もない状態で、フェイクニュースである確率」のことです。今回は問題文の中で、この確率は 0.4 であると明らかにされています。これは視覚的には、下図のように表すことができます。
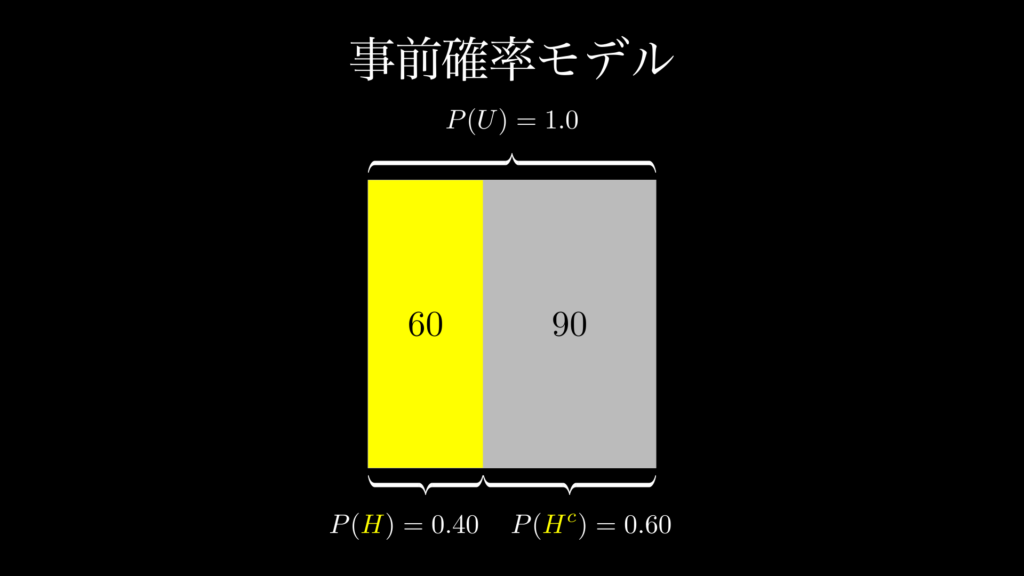
このように事前確率は、面積が 1 (150記事)の正方形を垂直に分割する割合です。これによって面積をフェイクニュースである 0.4(60 記事)と、フェイクニュースではない 0.6 (90 記事)に分けることができます。これを「事前確率モデル」と言います。
こういうふうに数学用語の意味を、国語的にだけではなく、幾何学的に理解しておくと、後になって非常に役に立ちますので、ぜひ覚えておいてください。
なお事前確率モデルは、以下の 3 つの条件を満たしている必要があります。
事前確率モデルの 3 つの条件
- モデル内に、その試行において起こりうる全ての事象が含まれている
- それぞれの事象に事前確率が設定されている
- 事前確率の合計は 1 である
2.2. 尤度を求める
続いて尤度(仮説 H が正しいとした時に、データ D を観察することがどれぐらいあり得るのか(尤もらしさ)を示す指標)を求めます。
この問題において、尤度 \(P(D|H)\) は、「フェイクニュースの中で、タイトルに!が付いているニュースを目にすることがどれぐらいあり得るのかを示す指標」です。これも問題文の中で 0.2667 であると与えられています。これは視覚的に表すと下図のようになっています。
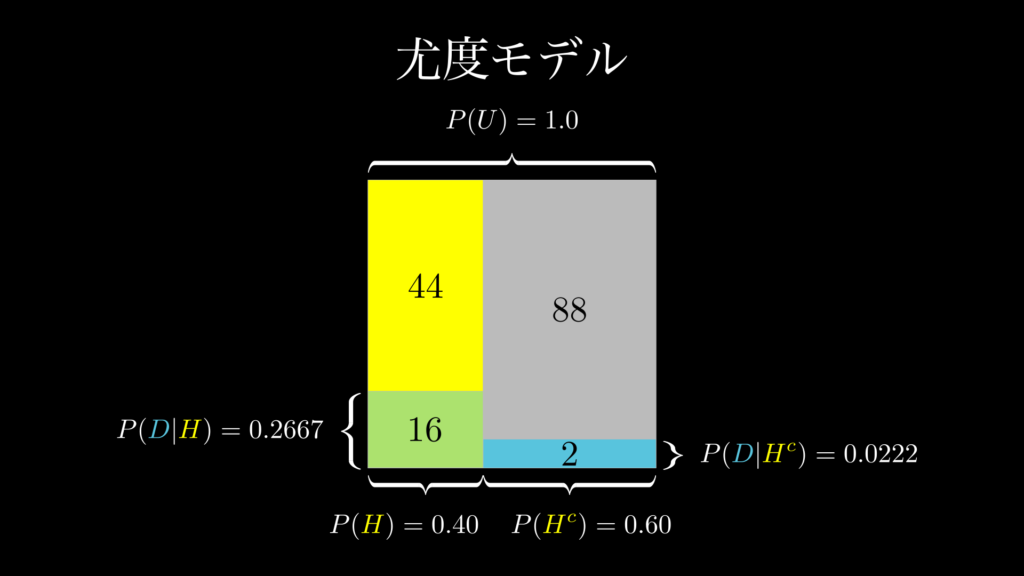
要するに、尤度は、フェイクニュースの面積 0.4(60記事)を 1 としたときの、!が付いている記事の割合です。具体的には、フェイクニュースの中で 60 記事 × 0.2667 ≒ 16 記事 が、タイトルに!が付いているものであるということを示しています。
そして、ベイズの定理の分子は、この尤度 \(P(D|H)\) と事前確率 \(P(H)\) を掛けたものです(0.4 × 0.2667 = 0.10668)。これは、ニュース記事全体の面積(150 記事)を 1 としたときの、フェイクニュースの中でタイトルに!が付いている記事の面積(上図 1.2 の緑の四角形の面積)になります。
一方で、問題文で与えられている 0.0222 という値は、フェイクではないニュースの中で、タイトルに!が付いているものの割合を示す尤度です。これも上図 1.2 をご覧頂ければ、どのようなものかが楽に理解できるでしょう。
なお尤度は厳密には確率ではないので、総和が 1 である必要はありません。
尤度は色々と難しく解説されている場合がほとんどですが、このように視覚的に見てみると、とても簡単な概念であることがわかります。尤度は、単純に仮説 H の中の D の割合、または仮説以外 H^c の中の D の割合に過ぎないのです。
2.3. 周辺尤度を求める
次に周辺尤度(仮説 H の真偽を問わず、データ D を観察する可能性)を求めます。
この問題において、周辺尤度 \(P(D)\) とは、「記事タイトルに!が付いているニュースを観察する可能性」のことです。これは視覚的には下図 1.3 の通り、面積が 1 の正方形の中の、青の四角形の合計割合のことです。
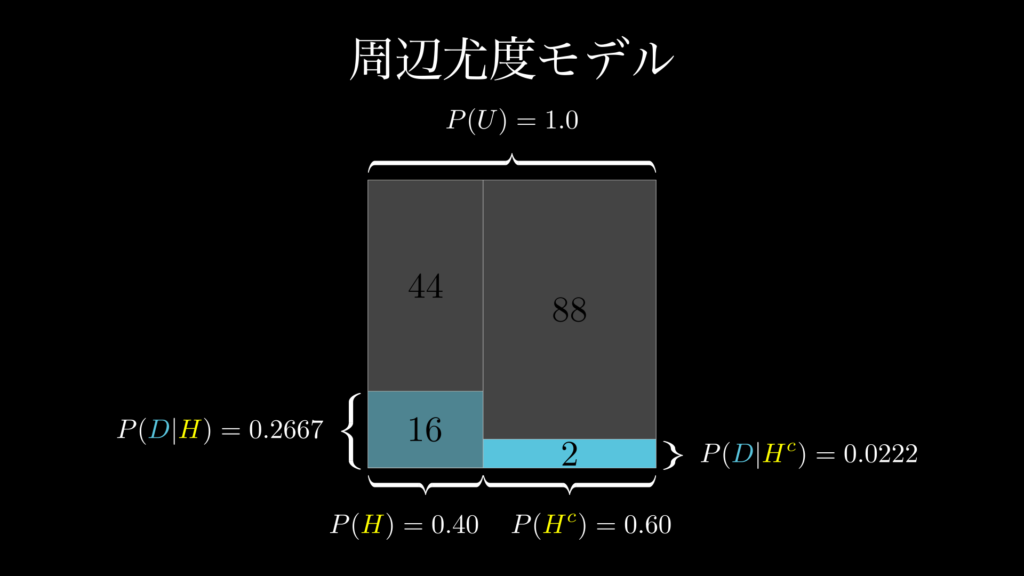
この図から、周辺尤度は以下の通り計算できることがわかります。
\[\begin{eqnarray}
P(D)
&=&
P(H)P(D|H)
+
P(H^c)P(D|H^c)\\
&=&
0.40\cdot0.2667 + 0.60\cdot 0.0222
=
0.12
\end{eqnarray}\]
これが、周辺尤度「仮説 H の真偽を問わず、データ D を観察することの可能性」が意味するものです。このように図を描きながら視覚的に考えると、言葉だけではなかなか理解しにくい概念も、とても簡単なものであることがわかります。
2.4. 事後確率を求める
最後に事後確率(事前に得たデータ D を踏まえて、仮説 H が正しい確率)を求めます。
事後確率は、「タイトルに!が付いているニュースが、フェイクニュースである確率」です。ここまで来れば、もう簡単です。下図 1.4 の通り割り算を行えば良いのです。
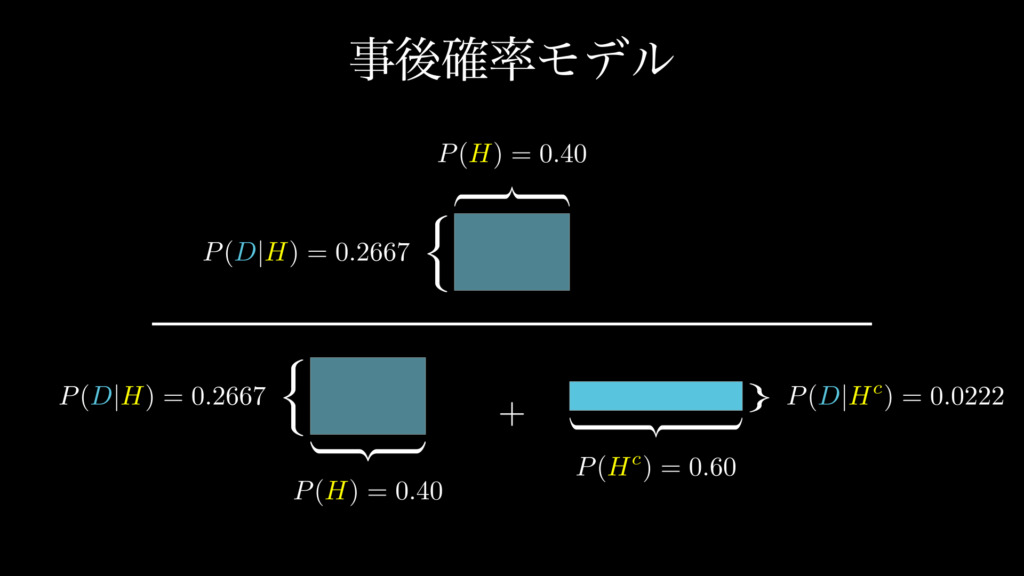
まず、分子は「ニュース記事全体における、フェイクニュースでありタイトルに!が付いているニュースの割合」です。ご覧の通り、これは事前確率 0.40 × 尤度 0.2667 で求められます。
次に分母は、先ほど求めた周辺尤度「ニュース記事全体における、記事タイトルに!が付いているニュースの割合」と同じです。
以上のことから事後確率「タイトルに!が付いているニュースが、フェイクニュースである確率」は次の通り求められます。
\[\begin{eqnarray}
P(H|D)
&=&
\dfrac{P(H)P(D|H)}{P(D)}\\
&=&
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac{0.40\cdot0.2667}
{0.40\cdot0.2667 + 0.60\cdot 0.0222}\\
&=&
0.889
\end{eqnarray}\]
このように分解して図を描いて見れば、ベイズの定理は簡単に解けることがわかります。
3. ベイズの定理の練習問題
ここではベイズの定理の使い方の理解を深めるために、ちょうど良い練習問題を 3 つ用意しています。どれもベイズの定理の代表的な問題であり、ベイズの定理がどれだけ優れているのかが体感できるものになっています。
確実に理解が深まりますので、ぜひ一度、挑戦してみてください。なお、その際は、上で解説したような図を実際に描いてみましょう。またベイズの定理は次の 4 ステップで解くことも意識して、解き進めてください。
- 事前確率を求める
- 尤度を求める
- 周辺尤度を求める
- 事後確率を求める
それでは始めましょう。
3.1. 医療検査で陽性のときの真の罹患率
病気の罹患率問題は、ベイズの定理を学ぶときの定番です。以下のような問題です。
問題:病気の真の罹患率
1 万人に 1 人だけがかかる難病があるとします。そして、この難病の罹患者に対して行うと 95 % の精度で陽性かどうかを判別できる検査があります。ただし、この検査を非罹患者に対して行った場合は 2 %の確率で偽陽性になってしまいます。さて、この検査で陽性反応が出た人が、実際に罹患者である確率はどれぐらいでしょうか。
まず、この問題では、検査で陽性の人が、実際に罹患者である確率を求めるので、仮説 H とデータ D は、それぞれ以下の通りになります。
- 仮説 \(H\):難病に罹患している
- データ \(D\):検査で陽性である
事前確率を求める
事前確率 \(P(H)\) は、「検査に関係なく病気に罹患している確率」です。これは問題文の「1 万人に 1 人だけがかかる」という文言があることから 0.0001 であると判断できます。
- 事前確率 \(P(H)=0.0001\) :検査を受ける前に難病に罹患している確率
尤度を求める
尤度 \(P(D|H)\) は、「病気に罹患している場合に、陽性判定が出ることの起こりやすさ」です。これも文中で 0.95 であることが明かされています。そして、「病気に罹患していない場合に、陽性判定が出ることの起こりやすさ(偽陽性率)」は 0 .02 です。
- 尤度 \(P(D|H)=0.95\):難病に罹患していて、検査陽性になることの起こりやすさ(真陽性率)
- \(P(D|H^c)=0.02\):難病に罹患していない場合で検査陽性になることの起こりやすさ(偽陽性率)
周辺尤度を求める
周辺尤度は \(P(D)\) は、「データを観察することの起こりやすさ」です。これは以下の計算で求められます。
- \(\begin{eqnarray}
P(D)&=&P(H)P(D|H)+P(H^c)P(D|H^c)\\
&=&0.0001\cdot 0.95 + 0.9999 \cdot 0.02
\end{eqnarray}\)
ここまでを視覚的に描いたものが下図です。
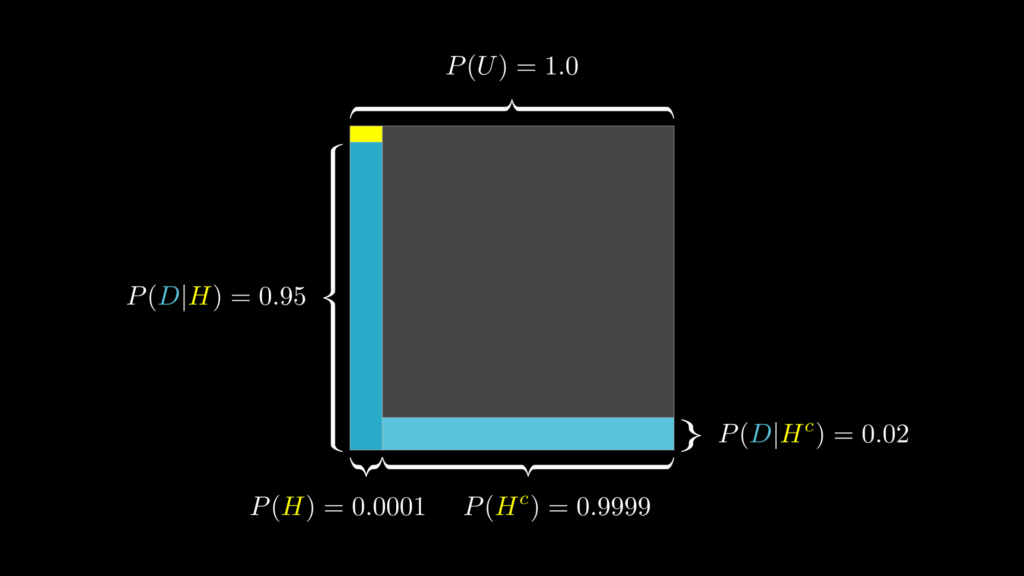
事後確率を求める
これでベイズの定理の計算に必要なパーツが全て揃ったので、事後確率を求めてみましょう。
\[\begin{eqnarray}
P(H|E)
&=&
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac
{
0.0001 \times 0.95
}
{
0.0001 \times 0.95
+
0.9999 \times 0.02
}\\
&\approx &
0.0047
\end{eqnarray}\]
この通り、陽性反応が出ても、実際に病気に罹患している確率は、たったの 0.47% であるということがわかりました。追加検査は受けるべきですが、まだそこまで不安がるような確率では全くありません。
3.2. モンティ・ホール問題
続いて、ベイズの定理でよく使われる問題であり、多くの数学者が答えを間違ったことで有名なモンティ・ホール問題を紹介します。
問題:選択肢を変えるべきか?
クイズ番組で、回答者は 3 つのドアのうち、1 つ選ぶ権利が与えられています。3 つのドアのうち 1 つのドアの後ろには商品である車が、残りの 2 つのドアの後ろにはヤギが置かれています。回答者は、まず 1 つのドアを選びます。その後、ドアの後ろに何があるのかを知っている司会者のモンティ・ホールは、選ばれなかった 2 つのドアのうち 1 つを開けます。このとき必ずヤギがいるドアが開けられます。そして司会者は回答者にこう聞きます。「開いていないもう 1 つのドアに選択を変えますか?」
果たして、選択を変えることは得なのでしょうか。
この問題は、まず 3 つのドアを、それぞれ A, B, C として、回答者が選ぶドアを A、司会者が開けるドアを B 、正解のドアを C とします。そうすると、仮説 H と データ D は次のようになります。
- 仮説 \(H_c\):ドア C が当たりである
- データ \(D\):司会者がドア B を開けた
事前確率を求める
事前確率 \(P(H_c)\) は、「司会者がドア B を開ける前の段階で、ドア C が当たりである確率」です。当たりドアは 3 つに一つですから、当然 1 / 3 になります。
- 事前確率 \(P(H_c)=0.33\):司会者がドア B を開ける前の段階で、ドア C が当たりである確率
- 事前確率 \(P(H_a)=0.33\):司会者がドア B を開ける前の段階で、ドア A が当たりである確率
- 事前確率 \(P(H_b)=0.33\):司会者がドア B を開ける前の段階で、ドア B が当たりである確率
尤度を求める
尤度 \(P(D|H_c)\) は、「ドア C が当たりである場合に、司会者がドア B を開けることの起こりやすさ」です。回答者がドア A を選んで、当たりドアが C である場合、司会者はドア B 以外の選択肢はありません。従って、尤度は 1 になります。同じように、当たりドアが A の場合、B の場合の尤度も以下の通りになります。
- 尤度 \(P(D|H_c)=1\):ドア C が当たりである場合に、司会者がドア B を開けることの起こりやすさ
- \(P(D|H_a)=0.5\):ドア A が当たりである場合に、司会者がドア B を開けることの起こりやすさ
- \(P(D|H_b)=0\):ドア B が当たりである場合に、司会者がドア B を開けることの起こりやすさ
周辺尤度を求める
周辺尤度 \(P(D)\) は、「司会者がドア B を開けることの起こりやすさ」です。これは事前確率と尤度から次のように求められます。
- 周辺尤度 \(\begin{eqnarray}
P(D)
&=&
P(H_c)P(D|H_c)+P(H_a)P(D|H_a)+P(H_b)P(D|H_b)\\
&=&
0.33 \times 1 + 0.33 \times 0.5 + 0 \times 0.33=0.495
\end{eqnarray}\)
ここまでを視覚的に描いたものが下図です。
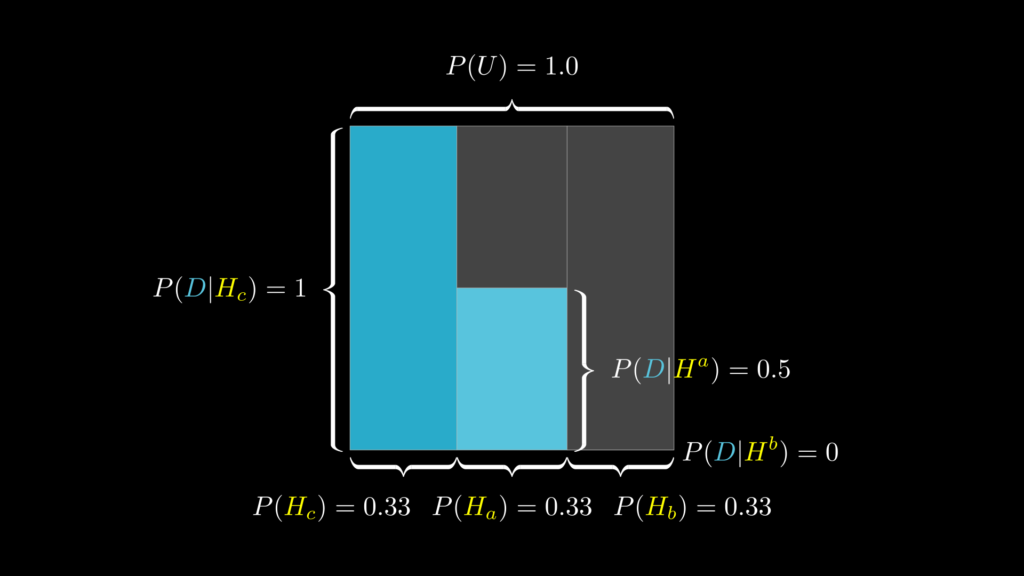
事後確率を求める
以上のことから、事後確率は次のように求められます。
\[\begin{eqnarray}
P(H|E)
&=&
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac
{
0.33 \times 1 + 0.33
}
{
0.33 \times 1 + 0.33 \times 0.5 + 0 \times 0.33=0.495
}\\
&\approx &
0.67
\end{eqnarray}\]
この通り、ドア C が当たりである確率が事前確率と比べて倍になるため、回答者は選択肢を変えるべきであるという結論になります。直感に反する答えに感じるかもしれませんが、実際にコンピューターで何万回とシミュレーションすると、確率はこの通りになることが確認できます。
3.3. 数学を知らない弁護士の失態
実は、ベイズの定理は、証言を正確に判断するためのツールとして、法廷でも使われます。この問題はその一例です。ぜひ挑戦してみてください。
問題:弁護のつもりが正反対の発言をした弁護士
ある殺人容疑で逮捕された容疑者の弁護士は、次のような主張をしました。
「この国では毎年 100 万人の妻が夫から虐待されています。そのうち虐待が原因で 400 人の妻が殺害されています。これは確率的には 0.0004 でしかありません。そのため被告人が妻を虐待していたからといって、殺害したことにはなりません」
果たして、この弁護士の主張は被告人にとって有利になるでしょうか。それとも不利になるでしょうか。なお、この国では毎年、100 万人当たり 450 人 の妻が何らかの原因で殺害されているとします(確率 0.00045)。
この問題は少しトリッキーです。この問題では、弁護士は夫が妻を虐待していたことは認めているわけですから、私たちが突き止めなければいけないのは、虐待されている妻が殺害される確率になります。そのため、仮説 H とデータ D は次の通りです。
- 仮説 \(H\):妻は夫から虐待を受けている
- 証拠 \(D\):妻が夫に殺害される
事前確率を求める
事前確率 \(P(H\) は、容疑者は妻を虐待していた事実があるわけですから 1 になります。
- 事前確率 \(P(H)=1\):妻が虐待を受けている確率
尤度を求める
尤度 \(P(D|H)\) は、「虐待を受けている妻が殺害されることの起こりやすさ」です。これはまさに弁護士が発言しているものです。弁護士は、「この国では毎年 100 万人の妻が夫から虐待されています。そのうち虐待が原因で 400 人の妻が殺害されています。これは確率的には 0.0004 でしかありません」と言っているわけですから、これは 0.0004 になります。
- 尤度 \(P(D|H)=0.0004\):虐待を受けている妻が殺害されることの起こりやすさ
周辺尤度を求める
周辺尤度 \(P(D)\) は、「妻が夫に殺害されることの起こりやすさ」です。今回は、これは問題文の中で既に明かされています。
- 周辺尤度 \(P(D)=0.00045\):妻が夫に殺害されることの起こりやすさ
ここまでを視覚的にまとめたものが下図です。
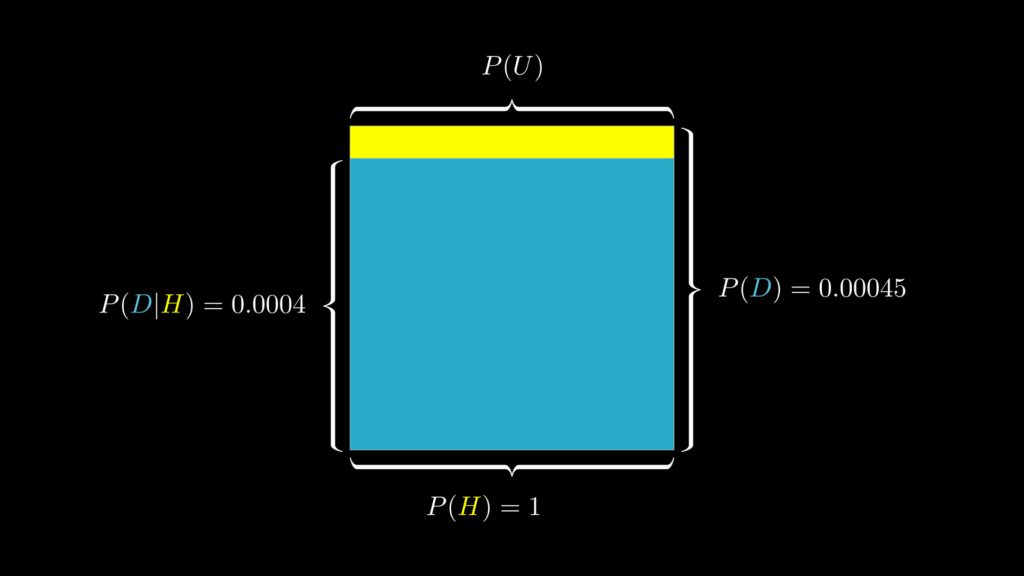
事後確率を求める
以上のことから事後確率 \(P(H|D)\)(殺害される妻が、夫からの虐待を受けている確率)は次の通り 89% になります。
\[\begin{eqnarray}
P(H|E)
=
\dfrac
{P(H)P(E|H)}
{P(E)}
=
\dfrac
{1\cdot 0.0004}
{0.00045}
\approx
0.89
\end{eqnarray}\]
以上のことから、この弁護士は「殺害された妻のうち、虐待を受けていた人の確率は 89% にも上る」と主張したことになります。つまり、容疑者を擁護するつもりが、さらに疑惑を深めることとなってしまったのです。
このようにベイズの定理は、直感的には間違って受け止めてしまいそうな場合でも、正しい確率を求めることを可能としてくれる技術なのです。
4. ベイズの定理の性質
練習問題を解いてきたことで、ベイズの定理についての理解がかなり深まったと思います。ここであらためて、ベイズの定理の性質について触れておきたいと思います。
最初の方で、ベイズの定理の本質は、「『事前知識は、新しいデータを吸収することによって、さらに優れた事後知識へと変わる』という点にある」とお伝えしました。ここでお伝えしたい性質は、これと関わるものです。具体的には、事前知識はどういう場合に変わり、どういう場合に変わらないのか、ということを示す性質です。ベイズの定理を扱う上で、この点を理解しておくことはとても役に立ちます。
それでは見ていきましょう。
4.1. 事前確率が影響を受けない場合
結論からお伝えすると、尤度(データ)が \(P(D|H)=P(D|H^c)\) の場合、データに関係なく事前知識と事後知識は変わりません
たとえば、フェイクニュースの問題を思い出してください。フェイクニュースもリアルニュースも同じぐらい記事タイトルに!が付いているとしたら(両者でデータが同じだとしたら)、当然、この「記事タイトルに!が付いている」というデータは、両者を見分けるための役には全く立たないことがわかります。そのため、この場合は、そのデータを受けても、事前確率には何の変化もありません。
実際に計算すると以下の通りになります。
\[\begin{eqnarray}
P(H|D)
&=&
\dfrac{P(H)P(D|H)}{P(D)}
=
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac{0.40\cdot0.30}
{0.40\cdot0.30 + 0.60\cdot 0.30}
=
0.40
\end{eqnarray}\]
これは視覚的には、下図のような状態になっています。
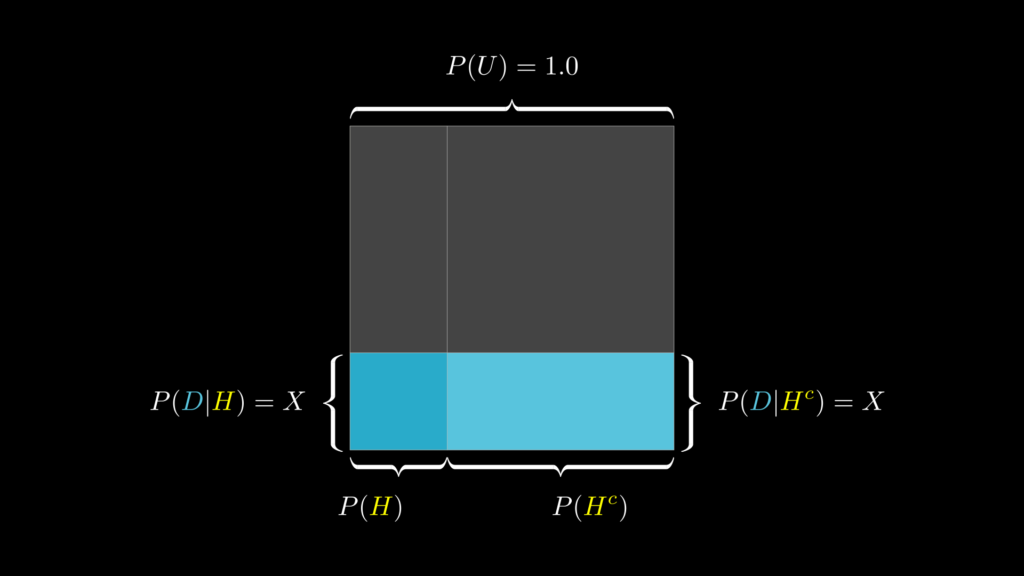
4.2. 事前確率が影響を受ける場合
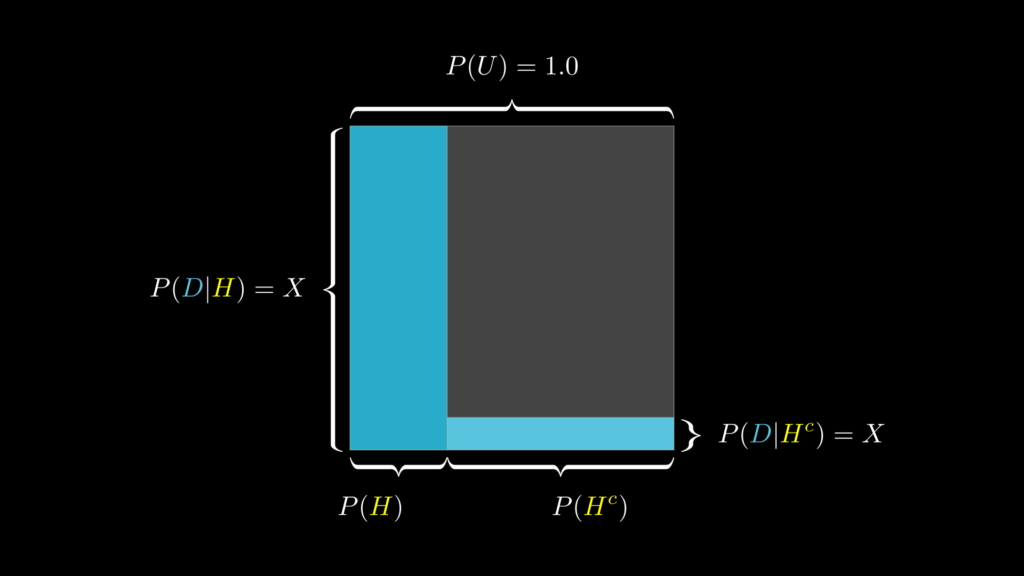
一方で、尤度が \(P(D|H)>P(D|H^c)\) となっており、この差が大きくなればなるほど、事前知識はデータを受けて大きく変わります(反対に、\(P(D|H)<P(D|H^c)\) で、この差が大きくなればなるほど、事前知識はデータを受けてもほとんど変わらなくなります)。
実際に計算すると以下の通りになります。
\[\begin{eqnarray}
P(H|D)
&=&
\dfrac{P(H)P(D|H)}{P(D)}
=
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac{0.40\cdot 1}
{0.40\cdot 1 + 0.60\cdot 0.10}
\approx
0.87
\end{eqnarray}\]
これは視覚的に表すと下図のようになっています。
これらは地味な知識に思われるかもしれませんが、覚えておくと、実際にベイズの定理を使って何らかのモデルを作る際に役立ちます。
5. ベイズ更新
最初の方で、ベイズの定理の第二の本質は、事前知識のアップデートを繰り返し行うことによって、どんどん知識が洗練されていく点であることを述べました。このプロセスを「ベイズ更新」と言います。
ベイズ更新は、厳密には「新しいデータを得たときは、前回に求めた事後確率を事前確率として使って、再計算をすること」です。下図をイメージして頂くと分かりやすいと思います。
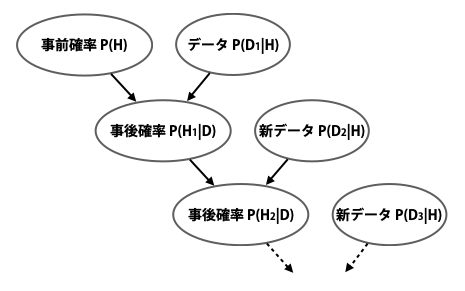
このベイズ更新は、コンピュータの処理能力が向上して、ビッグデータを扱えるようになった今、ベイズ統計が再脚光を浴びるようになった主な要因の 1 つです。なぜなら、これを行うために必要なのは、新しいデータと前回求めた事後確率だけであるため、以前のデータをすべて保管しておく必要はないからです。そのため計算を高速に行えますし、データを失うリスクに怯えることもありません。
通常の頻度論統計ではなかなかそうはいきません。なぜなら、頻度論の確率で再計算を行うには、過去の膨大なデータもすべて必要ですし、再計算の度に膨大なデータ量を扱うことになるので、コンピューターにも大きな負担がかかるからです。さらに、何らかの理由で過去データを失ってしまったら全ておしまいなのです。
ここでは上で用いた難病の罹患率の例を使って、実際にベイズ更新を行ってみましょう。
5.1. 二度目の医療検査の真の罹患率
問題:2度目の検査
X さんは、この検査を一度行って陽性反応が出ました。しかし、その上で、現時点で自分が本当に難病に掛かっているのか知りたくて、二度目の検査を希望しています。
さて、X さんが二度目の検査で陽性だった場合に、難病に罹患している確率はどれぐらいになるでしょうか。
なお一回目の計算の時のデータは以下の通りです。
- \(P(H|D)=0.0047\)
- \(P(H)=0.0001\)
- \(P(D|H)=0.95\)
- \(P(D|H^c)=0.02\)
この問題は次のように考えていきます。
まず、一度目の検査のとき、X さんが難病に罹患している事前確率は 0.0001 でした。しかし二度目の検査では X さんの事前確率は異なります。なぜなら、X さんは一度目の検査で既に陽性が出ているからです。そのため現段階で X さんが難病に罹患している事前確率は 0.0001 ではなく、 前回の事後確率である 0.0047 であることになります。
このことから、X さんが二度目の検査でも陽性の場合に、難病に罹患している事後確率は以下の計算で求められることになります。
\[\begin{eqnarray}
P(H|E)
&=&
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac
{
0.0047 \times 0.95
}
{
0.0047 \times 0.95
+
0.9999 \times 0.02
}\\
&\approx &
0.18
\end{eqnarray}\]
このように、 X さんが二度目の検査でも陽性だった場合、難病である可能性は 18%まで上がることがわかりました。簡単に行える検査であれば、悪くない数字ですが、物足りないのも事実です。
5.2. 三度目の医療検査の真の罹患率
それでは三度目の検査でも陽性だったらどうでしょうか?
問題:3 度目の検査
二度目の検査でも陽性だった場合に、三度目の検査を行って、そこでも陽性だった場合は、X さんが本当に難病に罹患している確率はどうなるでしょうか?
この場合は、2 度目の検査の時の事後確率を事前確率として使って再計算すれば良いので、以下のようになります。
\[\begin{eqnarray}
P(H|E)
&=&
\dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\
&=&
\dfrac
{
0.18 \times 0.95
}
{
0.18 \times 0.95
+
0.9999 \times 0.02
}\\
&\approx &
0.89
\end{eqnarray}\]
今回は 89% まで上がりました。これならわざわざ三度検査する価値はあると考えて良さそうです。
このように前回の事後確率を今回の事前確率として使い、より正確な新しい事後確率を導き出すのがベイズ更新です。繰り返しになりますが、これこれそが、今の時代にベイズ統計が再脚光を浴びるようになった大きな要因の一つです。
まとめ
最後に内容を軽くまとめておきます。
ベイズの定理とは
ベイズの定理とは「事前確率(もともと持っている信念や考え)が尤度(新しいデータや経験)を受けて、どう変化するのかを示す事後確率を求めるための方法」です。そして、このアップデートを繰り返し行うことで、事後確率はより洗練されたものになっていきます。これをベイズ更新と言います。
ベイズの定理を解くには、事前確率・尤度・周辺尤度を求めることが必要です。それぞれ計算上は次のような意味があります。
- 事前確率:\(P(H) \cdots\) 事前データ D が何もない状態で、仮説 H が正しい確率のことです。視覚的には、面積が 1 の正方形を縦に分割する際の割合を意味します。
- 尤度:\(P(D|H), \ \ P(D|H^c) \cdots\) 仮説 H が正しいとした時に、データ D を観察することがどれぐらいあり得るのかを示す指標です。視覚的には、P(H) によって縦に分割した四角形のそれぞれを、さらに横に分割する際の割合を意味します。
- 周辺尤度:\(P(H) \cdots\) 仮説 H の真偽を問わず、データ D を観察する可能性のことです。視覚的には、P(H) と P(D|H)、P(Hc) と P(D|Hc) で成り立つ 2 つの四角形の面積の合計を意味します。
事後確率 \(P(H|D)\) は、事前に得たデータ D を踏まえて、仮説 H が正しい確率であり、上の 3 つのパーツを使って次のように求めることができます。
\[\begin{eqnarray}
\small
事後確率
=
\dfrac{事前確率 \times 尤度}{周辺尤度}
\end{eqnarray}\]
以上がベイズの定理です。
ベイズの定理の性質
なお、ベイズの定理で、事前確率(信念や考え)が尤度(データ)によって、全く変わらないときと、大きく変わるときがあります。
まず全く変わらないときは、2 つの尤度がイコールのとき、つまり、\(P(D|H)= P(D|H^c)\) のときです。これ以外のときは、事前確率は変化しますが、もっとも大きく変化するのは、\(P(D|H)>P(D|H^c)\) であり、この差が大きくなるほど変化の仕方も大きくなります。
ベイズ更新
ベイズの定理は、一度事後確率を求めたら終わりというものではありません。次は、一度求めた事後確率を事前確率として用いることで、新しいデータを入手するたびに、事後確率を更新して洗練することができます。これをベイズ更新と言います。
これは頻度統計ではできないことであり、機械学習が全盛の時代にベイズ統計が脚光を浴びるようになった最大の要因であると言っても過言ではないほど重要な概念です。
以上がベイズの定理のまとめです。最後までご覧頂きありがとうございます。当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります(コメント返信は余裕ができれば行いたいと考えています)。


コメント
コメント一覧 (5件)
コロナのおかげでという言い方もおかしいのですが、コロナが発生したことがきっかけで、ベイズ統計学を勉強するきっかけになりました。それは、陽性的中率を計算するときに、ベイズ統計を使うからです。私は、ゴルフが好きで、今、女子プロゴルファーの、「バーディーだったとき、パーオンしている確率」と、「ボギー以下だったとき、パーオンしていない確率」を計算するのに、ベイズ統計の計算をしています。
ベイズ定理を使う必要に迫られまして、このサイトを発見いたしました。
非常に分かりやすい説明に感動いたしました。ありがとうございます。
なお、誤植と思われる箇所がありましたのでご報告いたします。
ご確認いただければ幸いです。
\begin{eqnarray} P(H|E) &=& \dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\ &=& \dfrac { 0.0001 \times 0.95 } { 0.0001 \times 0.95 + 0.9999 \times 0.02 }\\ &\approx & 0.0047 \end{eqnarray}
↓修正
\begin{eqnarray} P(H|E) &=& \dfrac{P(H)P(D|H)}{P(H)P(D|H)+P(H^c)P(D|H^c)}\\ &=& \dfrac { 0.0001 \times 0.95 } { 0.0001 \times 0.95 + 0.9999 \times 0.02 }\\ &\approx & 0.0047 \end{eqnarray}
\begin{eqnarray} P(H|E) &=& \dfrac{P(H)P(D|H)}{P(H^c)P(D|H^c)}\\ &=& \dfrac { 0.33 \times 1 + 0.33 } { 0.33 \times 1 + 0.33 \times 0.5 + 0 \times 0.33=0.495 }\\ &\approx & 0.67 \end{eqnarray}
↓修正
\begin{eqnarray} P(H|E) &=& \dfrac{P(H)P(D|H)}{P(H_c)P(D|H_c)+P(H_a)P(D|H_a)+P(H_b)P(D|H_b)}\\ &=& \dfrac { 0.33 \times 1 = 0.33 } { 0.33 \times 1 + 0.33 \times 0.5 + 0 \times 0.33=0.495 }\\ &\approx & 0.67 \end{eqnarray}
勉強になります。
1つ質問なのですが、P(H|E)のEって何を示しているのでしょうか。
P(H|D)=P(H|E)ですか?E=D?ですか?
視覚的にわかりやすく解説してくださりありがとうございます。
安全確保支援士でベイジアンフィルタリング(迷惑メールの検知手法)というものが出てきて、どんな定理なのか調べておりました。
3.3の事象で、周辺尤度は「妻が夫に殺害されることの起こりやすさ」ではなく、「妻が何らかにより殺害されることの起こりやすさ」ではないでしょうか?
また事後確率についても「殺害される妻が、夫からの虐待を受けている確率」だと問題にそぐわないように思います。「夫から虐待されていた妻が何者かに殺害されたとき、その犯人が夫である確率」としたほうが表現として理解しやすいように思いました。