定数倍の微分はとても簡単ですので軽視してしまいそうですが、他のより難易度の高い公式を理解できるようになるための土台となるので、実はとても重要なものです。
そこで、このページでは定数倍の微分公式について誰でもわかるように詳しく解説していきます。具体的には、以下のことがわかります。
- 関数の定数倍とはどのようなものか
- 定数倍の微分公式と数式による証明
- 定数倍の微分公式を直感的に理解できる方法
それでは始めましょう。
1. 関数の定数倍とは
最初に関数の定数倍について軽く復習しておきましょう。
関数 \(f(x)\) があるとき、定数を \(2\) としたら、その定数倍は \(2f(x)\) です。例えば、\(f(x)=\sin(x)\) なら、\(2f(x)=2\sin(x)\) です。これをグラフに描くと以下のように、高さが \(2\) 倍の曲線になります。
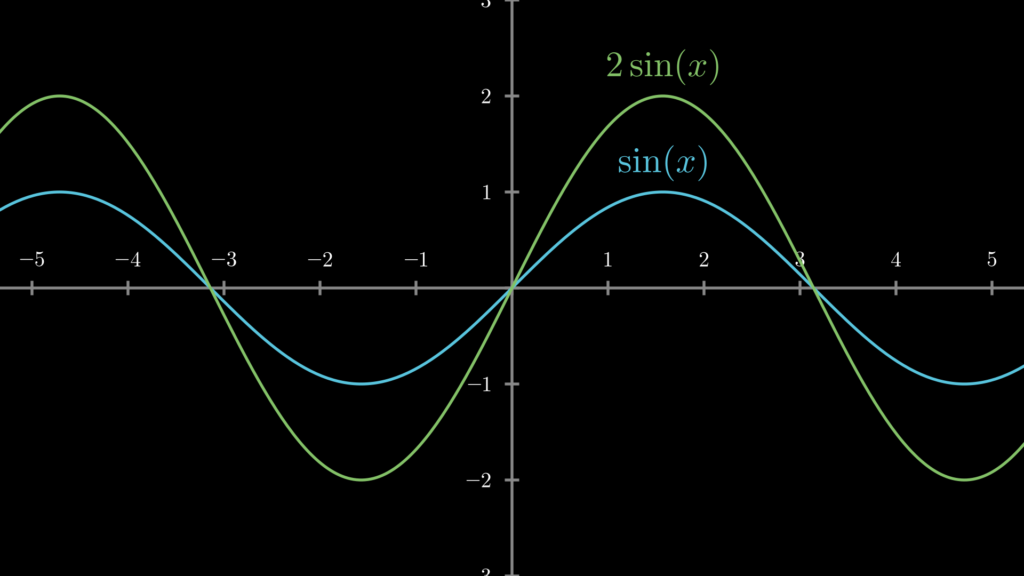
このように関数の定数倍は、曲線の高さを定数倍するものです。このことを理解していれば、関数の定数倍の微分はとても簡単に理解することができます。
2. 定数倍の微分公式と証明
関数の定数倍の微分は、以下の通りになります。
定数倍の微分法則
\[\begin{eqnarray}
\{\mathrm{c}f(x)\}^{\prime} = \mathrm{c}f^{\prime}(x)
\end{eqnarray}\]
例えば、\(f(x)=\sin(x)\) としたら、\(\{f(x)\}^{\prime}=\cos(x)\)、\(\{2f(x)\}^{\prime}=2\cos(x)\) となります。上で見たグラフからも明らかな通り、関数の定数倍では、曲線の高さが定数倍になるので、全ての地点で接線の傾きが倍になるのです。
このことは、微分の定義式からも簡単に証明することができます。
定数倍の微分法則の証明（微分の定義式より）
\[\begin{eqnarray}
\{\mathrm{c}f(x)\}^{\prime}
&=&
\dfrac{\mathrm{c}f(x+dx)-\mathrm{c}f(x)}{dx}\\
&=&
\dfrac{\mathrm{c}\{f(x+dx)-f(x)\}}{dx}\\
&=&
\mathrm{c} \dfrac{f(x+dx)-f(x)}{dx}\\
&=&
\mathrm{c} f^{\prime}(x)
\end{eqnarray}\]
3. 定数倍の微分公式の視覚的解説
定数倍の微分法則はとても簡単で当たり前のように理解できるものなので、特に視覚的（幾何学的）に理解しようとする必要はありません。しかし、その簡単さから微分を視覚的に把握するための練習としては、とても適しています。
以下の短いアニメーションをご覧頂ければ、定数倍の微分がどのようなものなのかを、視覚的に簡単に理解することができるでしょう。
そのため、ぜひ一度はご覧になってみてください。
4. 定数倍の微分公式のまとめ
以上が定数倍の微分公式です。とても簡単なので軽視してしまうかもしれませんが、このような基礎をしっかり理解しておくことは、他のより難易度の高い公式を理解できるようになるための土台となります。
ぜひ、参考にして頂ければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント