指数関数の微分は、微分学の中でも面白いトピックであり、微分を実社会に活かすために重要な分野でもあります。そこで、このページでは、指数関数の微分について、できるだけ誰でも理解できるように詳しく解説していきます。
具体的には、このページでは以下のことがわかるようになります。
- 指数関数とは何かが簡潔にわかる。
- 指数関数の微分公式を深く理解できる。
- ネイピア数とは何かを、なぜ重要なのかがわかる。
- 指数関数の底をネイピア数に変換する方法がわかる。
- 指数関数の底をネイピア数に変換することの重要性がわかる。
それでは早速始めましょう。
1. 指数関数とは
まずは指数関数について簡潔におさらいしておきましょう。関数は、現実世界のさまざまな現象の性質を表す、とても興味深いツールです。その中で指数関数は、細胞分裂や蓮の葉の増殖・複利金利・放射性物質の寿命・熱伝導など、非常に多くの現象を示す関数として有名です。
具体的には、指数関数は \(y=a^x\) で表されます。 \(a\) の部分を「底」、\(x\) の部分を「指数」と言います。
指数関数
\[
y=a^x\\
{}_{a>0, \ a \neq 1}
\]
一見すると、べき乗関数の \(y=x^n\) と似ていますが、指数関数は変数 \(x\) が指数部分に送られている点が異なります。そのため、べき乗関数とは全く異なります。参考に、以下のグラフは指数関数とべき乗関数を描いたものです。
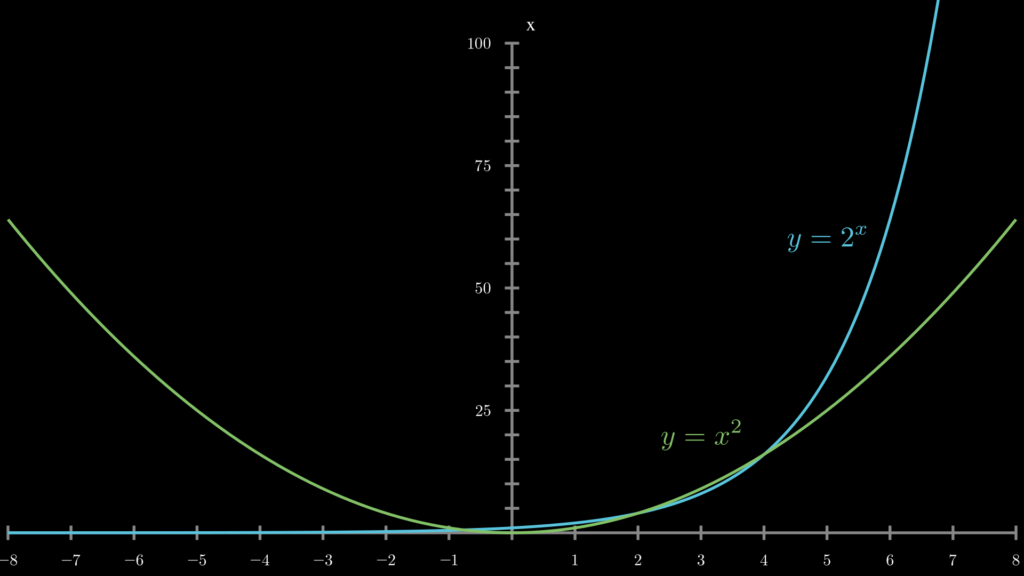
このように指数関数は、べき乗関数と比べて、比較にならないほど爆発的に値が増加していきます。
ここで一つ指数関数のことがよくわかるクイズに挑戦してみましょう。
例えば、あるウイルスが1つ存在していたとします。10分後、このウイルスの数が1024にまで増えていたとします。それでは、ウイルスの数が半分の512だったのは、いつの時点でしょうか。
おそらく多くの人が、反射的に5分辺りの時点だと考えたと思います。しかし、実際の答えは9分の時点です。なぜ、この答えになるのかは以下のグラフを確認頂くと、すぐにわかります。
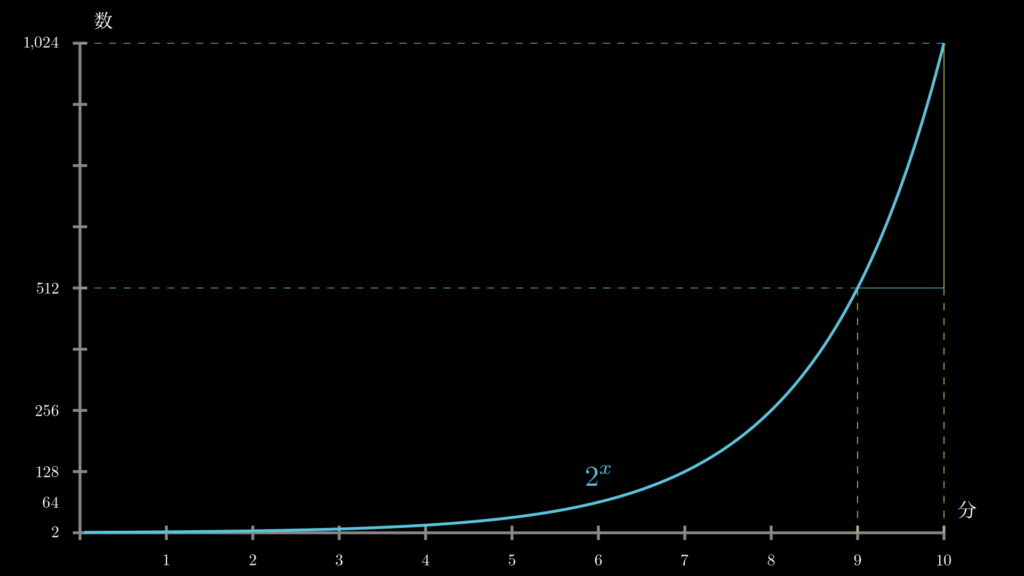
つまり指数関数 \(a^x\) では、ある時点 \(x+1\) 時点での値は、\(x\) 時点の \(a\) 倍になるのです。 ウイルスなどの爆発的な増殖を「指数関数的」と表現するのは、このためです。
なお、指数関数の底 \(a\) は、0 より大きく、かつ、1ではない数である必要があります。なぜなら \(0^x\) は常に \(0\) になり、\(1^x\) は常に \(1\) になるからです。そして、底の値が大きいほど曲線の傾きが急になります。しかし、\(0<a<1\) の範囲では逆になります。
以下の画像で示している通りです。
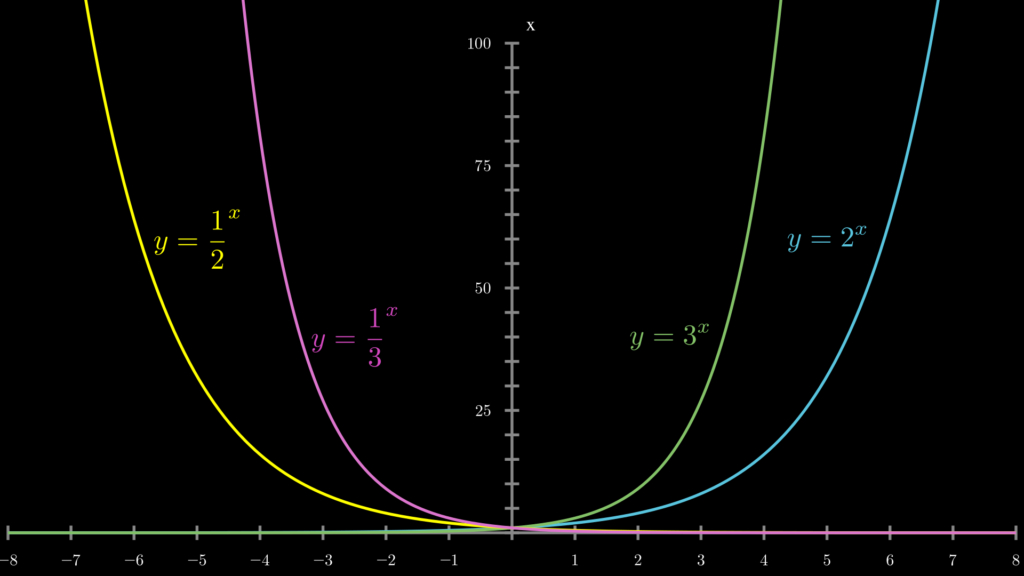
以上が指数関数です。
2. 指数関数の微分
さて、それでは指数関数の微分は一体どうなるでしょうか。ここでは、まず公式を示し、その後に、なぜその公式で求められるのかを詳しく解説していきます。
なお、先に解説しておくと、指数関数の微分公式は、底がネイピア数 \(e\) である場合と、それ以外の場合で異なります(厳密には同じなのですが、性質上、ネイピア数が底の場合の方がより簡単になります)。
ここではネイピア数とは何かという点についても解説するので、ぜひ読み進めてみてください。
2.1. \(a^x\) の微分
まず、底がネイピア数ではない指数関数 \(a^x\) の微分は、以下の公式で求めることができます。
底がネイピア数以外のとき
\[\begin{eqnarray}
(a^x)^{\prime} = a^x \log_ea\\
{}_{(※a>0 , \ a \neq 1)}
\end{eqnarray}\]
なぜこうなるのでしょうか。これは、まずは微分の定義式を使って求めてみることで、すぐに理解できるようになります。
以下のように指数関数を定義式に沿って微分すると、その解は前半部分の \(a^x\) と、後半部分の \(\frac{a^{dx}-1}{dx}\) に分けられることがわかります。
指数関数の \(a^x\) の微分を定義式から求める
\[\begin{eqnarray}
(a^x)^{\prime}
=
\dfrac{d}{dx}a^x
&=&
\dfrac{a^{x+dx}-a^x}{dx}\\
&=&
\dfrac{a^{x}a^{dx}-a^x}{dx}\\
&=&
a^x
\left(
\dfrac{a^{dx}-1}{dx}
\right)
\end{eqnarray}\]
※2段目は指数関数の公式 \(a^{m+n}=a^{m}a^{n}\) より求められます。
見ての通り、前半部分は対象の指数関数が \(2^x\) なら \(2^x\) のままですし、\(4^x\) なら \(4^x\) のままです。それでは後半部分はどうなるでしょうか。 \(a=2, \ 4, \ 8\) の場合で、実際に計算してみましょう。
すると以下のような定数が現れます。
定数部分の算出
\[\begin{eqnarray}
\dfrac{2^{dx}-1}{dx}=\dfrac{2^{0.000\cdots01}-1}{0.000\cdots01}=0.69314718 \cdots\\
\dfrac{4^{dx}-1}{dx}=\dfrac{4^{0.000\cdots01}-1}{0.000\cdots01}=1.38629436 \cdots\\
\dfrac{8^{dx}-1}{dx}=\dfrac{8^{0.000\cdots01}-1}{0.000\cdots01}=2.07944154 \cdots
\end{eqnarray}\]
なお、この計算がどういうことかわからないという場合は、あらためて『微分とは何か?わかりやすくイメージで解説』をご覧ください。
さて、以上のことから \(2^x, \ 4^x, \ 8^x\) の微分は、それぞれ以下の通りになります。
\(2^x, \ 4^x, \ 8^x\) の微分
\[\begin{eqnarray}
(2^x)^{\prime} &=& 2^x(0.69314718 \cdots)\\
(4^x)^{\prime} &=& 4^x(1.38629436 \cdots)\\
(8^x)^{\prime} &=& 8^x(2.07944154 \cdots)\\
\end{eqnarray}\]
ここで定数部分に注目してみましょう。何か興味深いことに気づかないでしょうか。
そう、\((4^x)^{\prime}\) の定数部分は、\((2^x)^{\prime}\) の定数部分の2倍に、そして、\((8^x)^{\prime}\) の定数部分は、\((2^x)^{\prime}\) の定数部分の3倍になっているのです。これは、\(4=2^2, \ 8=2^3 \) という関係性と合致しています。
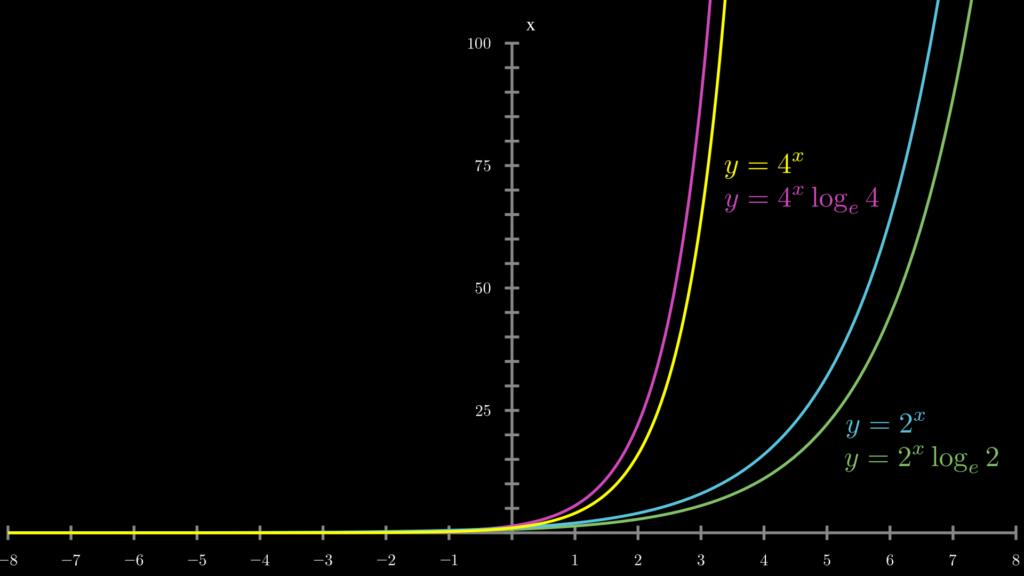
このような関係性が見られる場合、この定数は決してランダムな値ではなく、何らかの法則性のある値であると考えられます。そして結論から言うと、この定数部分は、それぞれの底に対する自然対数 \(\log_{e}a\) になっています(こうなる理由については、次のネイピア数を底とする指数関数の微分の項で解説します)。
以上のことから \((a^x)^{\prime}=a^x \log_{e}a\) となります。
2.2. ネイピア数の微分
続いて、ネイピア数 \(e\) を底とする指数関数の微分公式を見てみましょう。
ネイピア数とは、簡単に言うと、自然対数を取ると \(1\) になる値のことです。つまり、以下の条件を満たす値であるということです。
ネイピア数とは自然対数が\(1\)になる数
\[\begin{eqnarray}
\log_{e}a=\dfrac{a^{dx}-1}{dx}=\dfrac{a^{0.000\cdots01}-1}{0.000\cdots01}=1
\end{eqnarray}\]
別の言い方をすると、 \((a^x)^{\prime}=a^{x}\log_{e}a=a^x(1)\) になるような、指数関数の底 \(a\) は何かということです。
そして、この条件を満たす値を計算すると \(2.71828 \cdots\) という無理数が導き出されます。これの自然対数を取ると \(\log_{e}2.71828\cdots = 1\) になります。
これがネイピア数であり、記号の \(e\) で表されます。
このネイピア数は、指数関数の微分において、とても重要な数です。これがあるおかげで指数の変化の影響のみに注目して分析することができるようになっています。詳しくは後述しますので、ここではネイピア数は重要な数であるということだけ理解していれば良いでしょう。
\(e^x\) の微分
さて、このネイピア数を底とする指数関数を微分すると、以下の通り、何も代わりません。
底がネイピア数 \(e\) の指数関数の微分公式
\[\begin{eqnarray}
(e^x)^{\prime} = e^x
\end{eqnarray}\]
なぜなら、\(\begin{eqnarray}
(e^x)^{\prime}
&=&
e^x (\log_{e}e)
&=&
e^x(1)
&=&
e^x
\end{eqnarray}\) となるからです。以上のことから \((e^x)^{\prime}=e^x\) になります。
これは視覚的には、指数関数と導関数がまったく同じである(その時点での微分が、その時点での曲線の高さとイコールである)ということを意味しています。
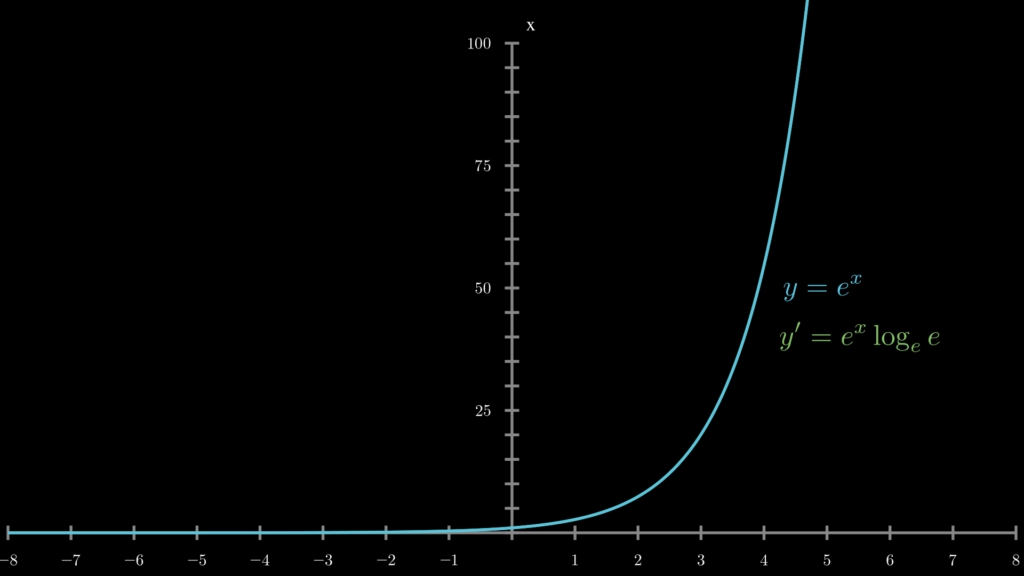
このようになるのは指数関数の中で \(e^x\) だけであり、この事実からネイピア数がどれだけ特殊な数であるのかを推し測ることができます。
\(e^{cx}\) の微分
それでは、\(e^{2x}, \ e^{3x}\) のように \(e^{cx}\) となった場合の微分はどうなるでしょうか。これは以下の公式の通りになります。
\(e^{cx}\) の微分公式
\[\begin{eqnarray}
(e^{cx})^{\prime} = ce^{cx}
\end{eqnarray}\]
これは単に、\(g(h)=e^h\) と \(h(x)=cx\) の合成関数 \(g(h(x))\) になっているだけです。そのため、合成関数の微分公式で解くことができます。
もし、\(e^{cx}\) が合成関数であるという点がわかりにくいと感じたら、『合成関数の微分を誰でも直観的かつ深く理解できるように解説』で解説しているように、関数 \(e^{cx}\) を以下のような数直線でイメージしてみてください。
さて合成関数 \(g(h(x))\)の微分は、\(g^{\prime}(h)h^{\prime}(x)\) で求められるので、これの微分は以下の通りに計算することができます。
合成関数 \(e^{cx}\) の微分
\[\begin{eqnarray}
(e^{cx})^{\prime}
&=&
\dfrac{d}{dh}e^{cx}\cdot \dfrac{d}{dx}cx\\
&=&
\dfrac{(e^{cx})^{\prime}(dh)}{dh} \cdot \dfrac{(cx)^{\prime}(dx)}{dx}\\
&=&
e^{cx} \cdot c \\
&=&
ce^{cx}
\end{eqnarray}\]
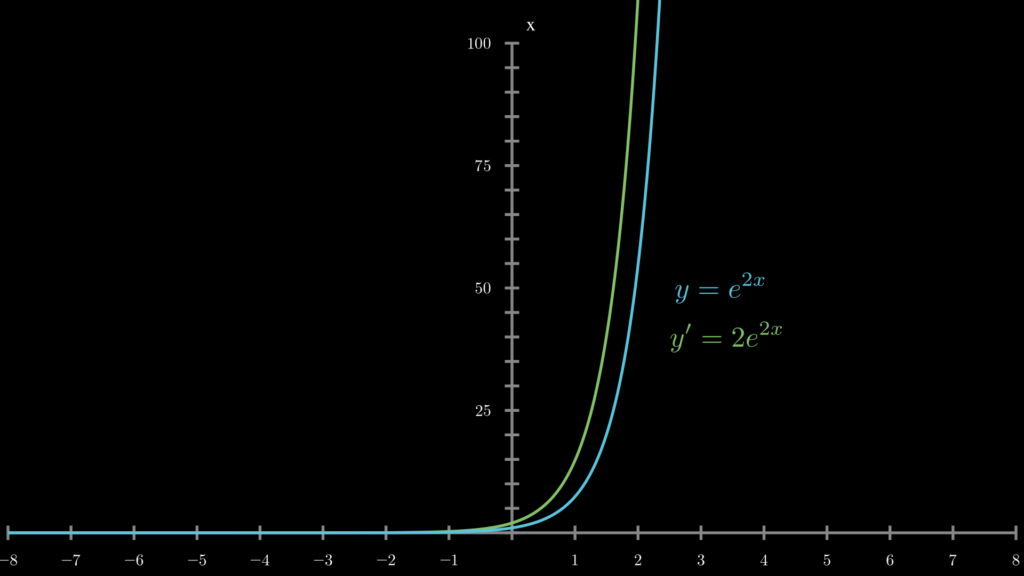
このように指数関数 \(e^{cx}\) の微分は \(ce^{cx}\) になります。
3. 指数関数の変換
指数関数の微分については以上の通りですが、ここではネイピア数についてもう一度考えていきましょう。
実は、微分の応用に進むと \(y=a^x\) の形の指数関数を扱うことはほぼありません。全ての指数関数を底をネイピア数に変換した \(y=e^{log_{e}(a)x}\) の形を扱うことになります。
なぜなら、指数関数の底をネイピア数 \(e\) に固定することで初めて、指数部分のみを比較対象として、さまざまな現象を区別して説明できるようになるからです。それによって、微分の比較計算がやりやすくなるという効果もあります。
わかりやすく言えば、\(2^{128}\) と \(10^{32}\) というように底が異なると、どちらが大きいのか小さいのかといった基本的なこともわからなくなってしまいますが、\(e^{128}\) と \(e^{32}\) なら、一目で比較できるということです。
そういうわけで、ここでは指数関数の底をネイピア数に変換して、その微分を求める方法を見ておきましょう。
3.1. 底をネイピア数に置き換え
まず、指数関数の底をネイピア数に変換するには、以下の公式を使います。
指数関数の底をネイピア数 \(e\) に変換する公式
\[
a^x=e^{\log_e(a)x}
\]
このように指数関数の変換は、底をネイピア数 \(e\) に、指数を自然対数 \(log_{e}a\) に置き換えるという方法で行うことができます。
なぜ、こうなるのでしょうか?
ここまで解説してきた通り、ネイピア数 \(e\) は、その自然対数が \(1\) になる値です。そして、通常の算数では \(1\) を基準にすると、あらゆる数値を直観的に理解できるようになるのと同じように、指数関数でも \(e\) を基準にすると、あらゆる数値を直観的に理解できるようになります。
ネイピア数を底とする指数関数であらゆる数値を表すことができる
\[\begin{eqnarray}
2 = & e^{\log_e(2)} & = e^{0.6931 \cdots} \\
4 = & e^{\log_e(4)} & = e^{1.2862 \cdots} \\
8 = & e^{\log_e(8)} & = e^{2.0794 \cdots} \\
& \vdots & \\
n = & e^{\log_e(n)} &
\end{eqnarray}\]
これは何も特殊なことをしているわけではなく、自然対数の定義そのものです。単純に \(n= e^{\log_e(n)}\) なのです。このことから、以下に示しているように、\(a^x\) の形の指数関数の底はネイピア数 \(e\) に変換することができます。
あらゆる指数関数の底はネイピア数に変換できる
\[\begin{eqnarray}
2^x &=& e^{\log_e(2)x}\\
4^x &=& e^{\log_e(4)x}\\
8^x &=& e^{\log_e(8)x}\\
&\vdots&\\
a^x&=&e^{\log_e(a)x}\\
\end{eqnarray}\]
なお、余談ですが、指数関数を表す書き方は無限にあります。
\[2^x
=
e^{(0.6931\cdots)x}
=
e^{\log_e(2)x}
=
\pi^{(0.60551\cdots)x}
=
\pi^{\log_{\pi}(2)x}
=
42^{(0.18545\cdots)x}
=
42^{\log_{42}(2)x}
\]
しかし、皆がこうやって異なる底を使っていたとしたら、人それぞれに基準が異なることになってしまって、議論が進まなくなってしまいます。だからこそ、微分の応用では、比較がやりやすくなるという効果もあり、ほぼ全ての指数関数の底を \(e\) に置き換えて議論できるようにしているのです。
3.2. 自然対数の微分
さて、それでは、このように底をネイピア数に、指数部分を自然対数に変換した指数関数の微分はどのようになるでしょうか。以下の通りになります。
底を \(e\) に変換した指数関数の微分は公式通り
\[\begin{eqnarray}
(e^{\log_e(a)x})^{\prime}
&=&
(e^{\log_e(a)x})(\log_e(a))\\
&=&
a^x \log_e(a)
\end{eqnarray}\]
つまり、公式通りなのですが、\(e^{\log_e(a)x}\) の形にしておくと、底に気を煩わされることなく、指数部分(自然対数)に注目するだけで微分を行うことができるという利点があります。
利点は指数部分を見るだけで微分ができる点にある
\[\begin{eqnarray}
(e^{\log_e(2)x})^{\prime}
&=&
2^x \log_e(2)\\
(2^x)^{\prime} &=& 2^x \log_e(2)
\end{eqnarray}\]
最初はピンとこないかもしれませんが、このように底に気を払う必要がなくなるということは、とても大きな利点ですので、ぜひ頭に入れておいてください。
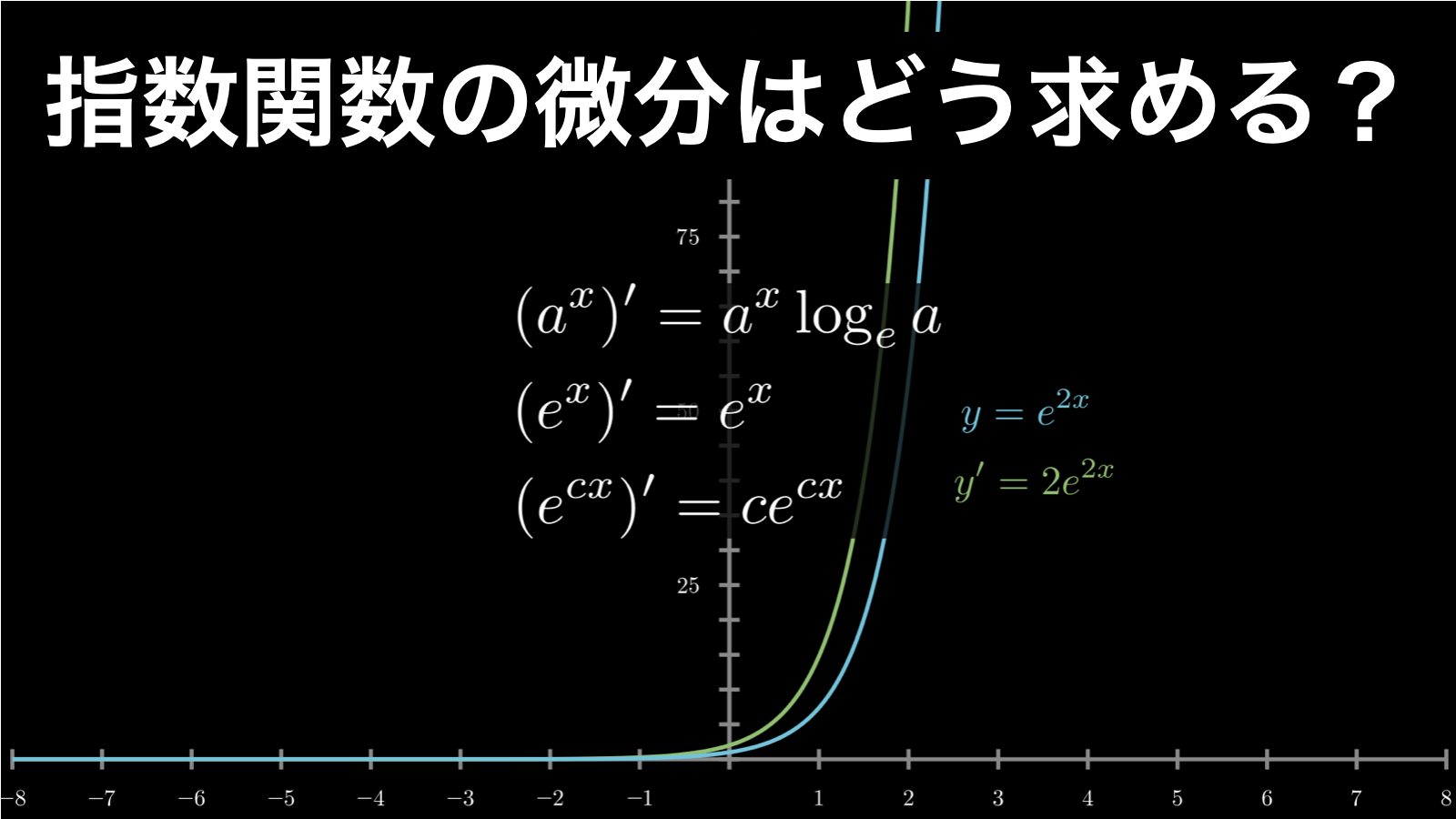
4. 指数関数の微分まとめ
以上が指数関数の微分です。重要な公式をもう一度まとめておきましょう。
\(a^x\) の微分公式
\[\begin{eqnarray}
(a^x)^{\prime} = a^x \log_ea\\
{}_{(※a>0 , \ a \neq 1)}
\end{eqnarray}\]
\(e^x\) の微分公式
\[\begin{eqnarray}
(e^x)^{\prime} = e^x
\end{eqnarray}\]
\(e^{cx}\) の微分公式
\[\begin{eqnarray}
(e^{cx})^{\prime} = ce^{cx}
\end{eqnarray}\]
指数関数の底をネイピア数 \(e\) に変換する公式
\[
a^x=e^{\log_e(a)x}
\]
受験勉強は、これらの公式を覚えてさえいれば乗り切ることができます。しかし、指数関数の微分を、実社会に役立つように応用しようとすれば、これらの微分がなぜこうなるのかをしっかりと理解しておく必要があります。
指数関数は、生物学から経済学・金融・コンピューターサイエンスなど、驚くほど多くの現象を説明することができる関数です。そのため、公式を盲目的に使うだけではなく、なぜそうなるのかをしっかりと理解できるように学習してみて頂ければと思います。
当ページがそのための役に立ったなら、とても嬉しく思います。




コメント