-

ベイジアン・ネットワークとは何か?をわかりやすく解説
ベイジアン・ネットワークとは、簡単に言うとものごとの因果関係を数学的にも視覚的にも明らかにしてくれる方法です。つまり、ある結果が起こったとして、その結果の原因と考えられる事象が、実際にはどれぐらい結果に関係していたのかを教えてくれるので... -

尤度の意味と計算方法をわかりやすく解説
尤度(読み方「ゆうど」 英語 "likelihood")は、機械学習で必ず出てきますし、近年になって一躍脚光を浴びているベイズ統計を理解する上でも必須の概念でもあります。しかし尤度の解説は、複雑なものばかりで、なかなか直感的に理解することはできません... -

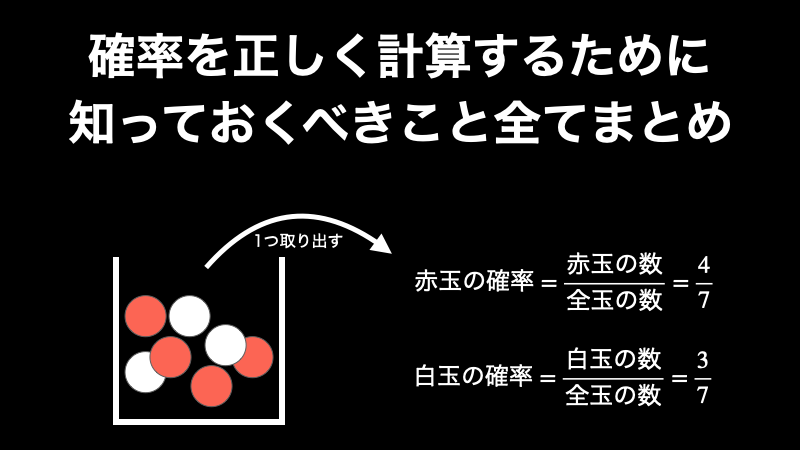
確率を正しく計算するために知っておくべきこと全てまとめ
確率とは、「偶然起こる現象が、起こりうる現象全ての中において、どれぐらいの割合を占めるのかを表す数値」であり、「現象の起こりやすさの指標」です。 この指標を使いこなすことで、私たちは、未来に何が起こりそうかを前もって予測し、現在の選択肢の... -

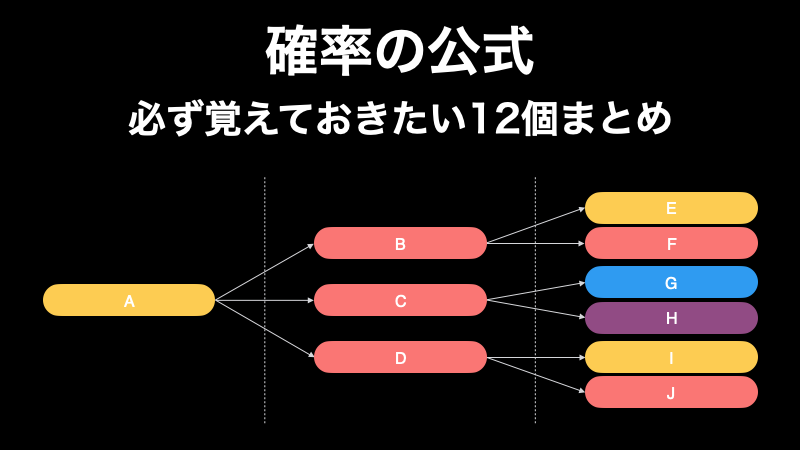
確率の公式 ~必ず覚えておきたい12個まとめ~
ここでは確率を効率的に求められるようになるために覚えておきたい 12 個の公式をまとめています。必要なときに見返すようにして使って頂ければと思います。 それでは前置きは抜きにして、早速見ていきましょう。 【0. 確率の基本用語と記号一覧】 確率に... -

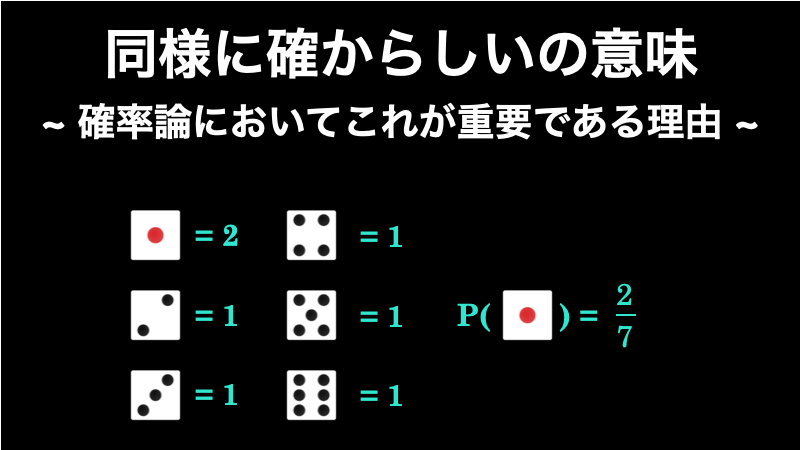
同様に確からしいの意味を誰でも理解できるようにわかりやすく解説
「同様に確からしい」とは、ある試行において起こりうる事象のすべてが「同じように起こる可能性があると考えられる」という意味です。たとえばコイントスでは、表の方が裏よりも出やすいということはなく、表が出る可能性と裏が出る可能性は同じであると... -

確率の求め方を誰でも理解できるようにわかりやすく解説
確率の求め方(計算方法)はとても簡単なのですが、公式だけを見ると、使われている言葉が難しそうで、なんだかとても難解なものに思えてしまいます。そこで、このページでは、本当は簡単なものである確率の求め方を誰でも理解できるように解説します。 そ... -

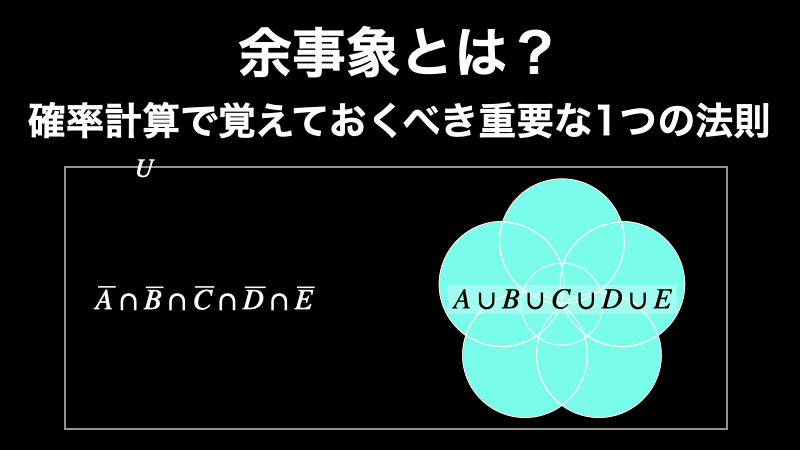
余事象とは何か?誰でも理解できるようにわかりやすく解説
余事象は、簡単に言うと「ある事象 A に対して、A ではない事象すべて(= A の正反対の事象)」のことです。言葉で表すとこれだけですが、実はこれは現実世界で確率を使いこなせるようになるために、必ずマスターしておくべき概念です。 なぜなら、この余... -

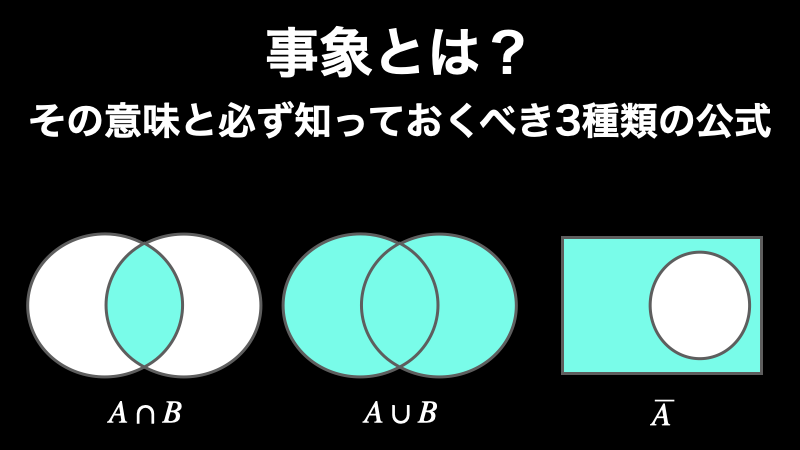
事象とは?その意味を誰でも理解できるようにわかりやすく解説
「事象」という言葉は確率論で登場する重要な概念です。簡単に言えば「出来事」のことなのですが、実はそれ以上に厳密な意味があります。そこで、このページでは、事象の意味を誰でも理解できるように詳しく解説します。そして事象について知っておくべき... -

組み合わせとは?誰でも理解できるようにわかりやすく解説
組み合わせとは、「n 個の異なる要素の中から r 個を取り出すときにあり得るパターン」のことです。主に数学の一分野である確率論や集合論、統計学で根幹となる分野であり、身近な例で言えば、ガチャやロトくじ、ブラックジャックなどのゲームで起こりうる... -

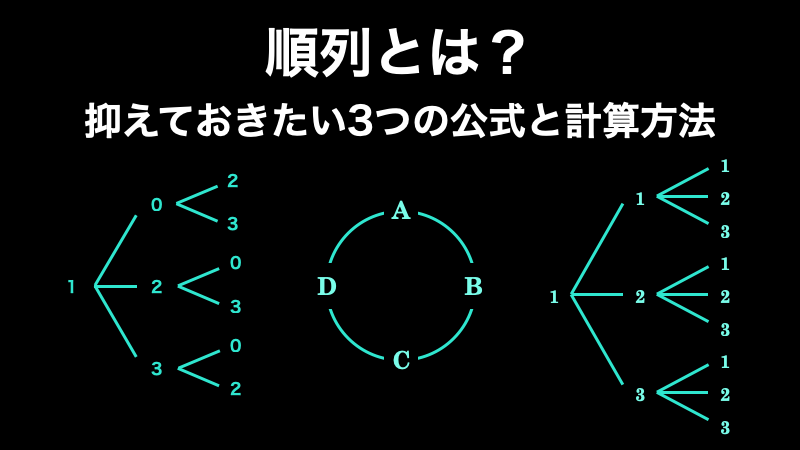
順列とは?理解しておきたい4つの公式と計算方法
順列は、n 個の要素の中から r 個を取り出すとして、あり得るパターンの数をかぞえ上げる方法の一つです。これは数学の基本の一つである「集合」や「場合の数」を求めるために欠かせないものであり、特に確率論や統計学を理解するための基本となる概念でも... -

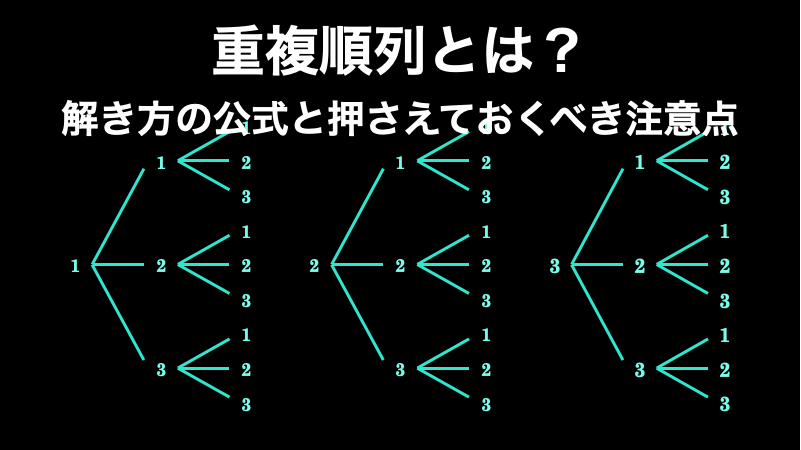
重複順列の公式と解き方と押さえておくべき注意点
重複順列は、「同じ要素を繰り返し使っても良い順列」です。つまり、要素が重複しても良い順列ということですね。このページでは、この重複順列の具体例・公式・練習問題を解説します。特に、重複順列の練習問題は慣れないうちは混乱しがちなので、そうな... -

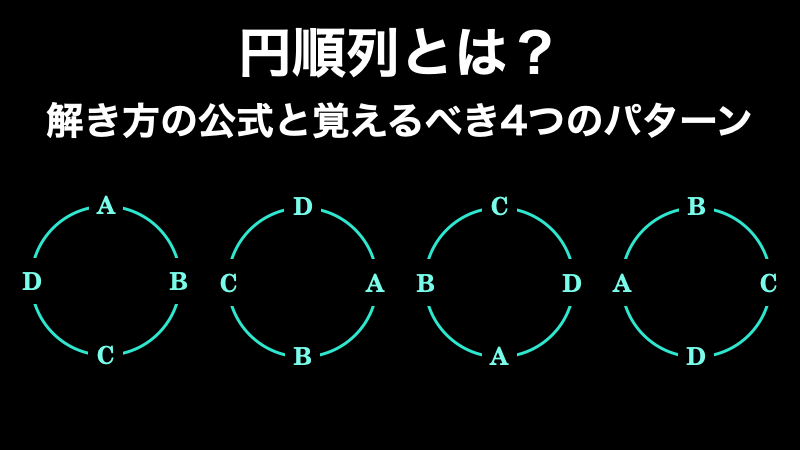
円順列とは?解き方の公式と覚えるべき4つのパターン
円順列は、文字通り、要素を円形に並べたもののことです。通常の順列とは異なって円形であるため、回転した場合に同じ並びになるものは 1 通りとして考えます。なお通常の順列は『順列とは?抑えておきたい3つの公式と計算方法』で解説しています。 当ペー...