ベイジアン・ネットワークとは、簡単に言うとものごとの因果関係を数学的にも視覚的にも明らかにしてくれる方法です。つまり、ある結果が起こったとして、その結果の原因と考えられる事象が、実際にはどれぐらい結果に関係していたのかを教えてくれるのです。
人の感覚は、結果と原因の関係を簡単に見誤ってしまいますが、数学を駆使することで、そのような見誤りを防ぐことができるのです。これには、とてつもなく大きな意義があります。
そこで、このページでは、このベイジアン・ネットワークについてどこよりも詳しく解説していきます。ぜひ参考にして頂ければと思います。
なお、最低限ベイズの定理の理解が必要なので、その理解に不安がある場合は、先に『ベイズの定理とは？証明や応用方法がよくわかる5つの例題』をご覧いただければと思います。
それでは始めましょう。
1. ベイジアン・ネットワーク
ベイジアン・ネットワークは、連鎖的に起こる物事の因果関係（連鎖的な確率）を求める方法であり、特に AI の分野では中核的な技術です。AI を学習すると必ず下図のようなニューラル・ネットワークを目にしますが、これこそまさにベイジアン・ネットワークを使って作られた概念なのです。
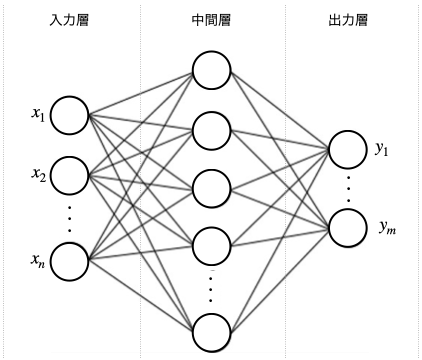
より詳しく解説していきます。
1.1. 事象間の因果関係の可視化
突然ですが「風が吹けば桶屋が儲かる」ということわざはご存知でしょうか。これは次のようなものごとの連鎖を表現したものです。
- 風が吹く
- 砂ぼこりが舞う
- 盲人が増える
- 三味線が売れる（盲人が趣味とするため）
- ネコが減る（三味線の材料となるため）
- ネズミが増える
- 桶が売れる
昔の人は、本気で、桶屋が儲かった原因は風が吹いたからだと思っていたのかもしれません。しかし、ちょっと考えれば、桶屋が儲かった原因を、風が吹いたことに求めるなんて、あまりにも馬鹿らしいことがわかります。
なぜなら数学的に考えて、両者の間に強い因果関係などないことは明らかです。そう、このことわざが真実なのかどうか、つまり「桶屋が儲かる」という事象は、「風が吹く」という事象が引き起こしているものなのかどうかを、数学的に診断できる方法があるのです。
もちろん、その方法こそがベイジアン・ネットワークです。つまり、ベイジアン・ネットワークとは、さまざまな事象の間の因果関係を、蜘蛛の巣状に可視化したものだということです。
それは、どのようにしたら可能になるのでしょうか。
1.2. 事象間の因果関係の求め方
ベイジアン・ネットワークでは、ある事象を「ノード」と呼ばれる ◯ で表します。そしてノード同士を矢印でつなげます。矢印の出元が原因、出先が結果です。
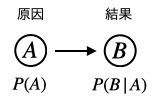
上図の簡単なネットワークは、事後確率 \(P(B|A)\) を表しています。仮に事象 \(A\) を風邪、事象 \(B\) を頭痛として考えると、\(P(B|A)\) は風邪を引いている時に頭痛が起こる確率を示しています。
ここで被験者が風邪である確率を 0.80 とすると、風邪でない確率は 0.20 になります。これをベイジアン・ネットワークでは、真 = 1 、偽 = 0 として、次のように表します。
- \(P(A:1)=0.80 \cdots\cdots\) 風邪である確率
- \(P(A:0)=0.20 \cdots\cdots\) 風邪でない確率
そして \(P(B|A)\) は、次の通りであることがわかっているとします。
- \(P(B:0 \ | \ A:0)=0.75 \cdots\cdots\) 風邪でない場合で頭痛がない確率
- \(P(B:0 \ | \ A:1)=0.10 \cdots\cdots\) 風邪である場合で頭痛がない確率
- \(P(B:1 \ | \ A:0)=0.25 \cdots\cdots\) 風邪でない場合で頭痛がある確率
- \(P(B:1 \ | \ A:1)=0.90 \cdots\cdots\) 風邪である場合で頭痛がある確率
さて、このとき風邪と頭痛の因果関係（頭痛の原因が風邪である確率）は、どのように求められるでしょうか。
これは尤度である \(P(A|B)\)（＝頭痛という結果から、前提条件が風邪であると推測することの尤もらしさ）を求めることでわかります。なお尤度については『尤度の意味と計算方法がよくわかる解説』で解説していますので、ぜひご確認ください。
そして、これはベイズの定理より以下の通り求められます。
\[
\begin{eqnarray}
P(A:1 \ | \ B:1)
&=&
\dfrac
{
P(B:1 \ | \ A:1)P(A:1)
}
{
P(B:1)
}\\
&=&
\dfrac
{
P(B:1 \ | \ A:1)P(A:1)
}
{
P(B:1 \ | \ A:1)P(A:1)
+
P(B:1 \ | \ A:0)P(A:0)
}\\
&=&
\dfrac
{
0.90 \times 0.80
}
{
0.90 \times 0.80
+
0.25 \times 0.20
}\\
&=&
0.935
\end{eqnarray}
\]
この通り、頭痛がある場合、その原因は 93.5% の確率で風邪であるということがわかりました。このようにベイジアン・ネットワークはものごとの因果関係を可視化してわかりやすくする概念なのです。
上の例はノードは 2 つだけでしたが、ノードが増えて複雑になった場合でも同じ計算で、ものごとの因果関係（連鎖確率）を数学的に算出することができます。
1.3. ベイジアン・ネットワークの例題
ベイジアン・ネットワークを、少しだけ複雑にしてみましょう。下図をご覧ください。
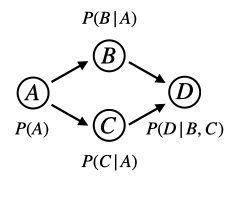
\(A\) から \(D\) の事象は、それぞれ起こるか（= 1 ）、起こらないか（= 0）があります。そして、それぞれの確率については、以下のようにデータが得られているとします（各ボックスをクリックしてご確認ください）。
さて、このようなデータが与えられている時、因果関係の計算のために使うベイズの定理の分母である周辺尤度（ \(P(B)\), \(P(C)\), \(P(D)\) ）は次のように求めます（各ボックスをクリックしてご確認ください。なお求め方の解説は「1.2. 周辺尤度｜ベイズの定理」で解説しています）。
さて、以上のようにデータがわかったとして、たとえば「\(D\) の原因が \(B\) であって、\(C\) ではない確率」を求めてみましょう。
これはベイズの定理より次の計算で求められます。
\[
\begin{eqnarray}
P(B:1 \cap C:0 \ | \ D:1)
&=&
\dfrac
{
P(D \ | \ B:1 \cap C:0) P(B:1 \cap C:0)
}
{
P(D)
}\\
&=&
\dfrac
{
0.82 \times 0.11
}
{
0.56
}\\
&=&
0.16
\end{eqnarray}
\]
このように「\(D\) の原因が \(B\) であって、\(C\) ではない確率」は 16%であると求められます。つまり、\(B\) のみが \(D\) の原因であるという考えは、根拠が弱いということになります。
このようにベイジアン・ネットワークを使うと、物事の因果関係を数学的に正しく求められるようになります。そして、ベイジアン・ネットワークは、因果関係を求めたい時であれば、どのような問題でも自由につくることができます。
もちろん、ネットワークが大きくなればなるほど、計算はどんどん複雑になりますが、どれだけ複雑なものになってもベイジアン・ネットワーク基本構造は、ここまで解説してきたものと全く変わりません。そのため、経験を積めば積むほど理解が深まり、あらゆるものの原因と結果の関係をベイジアン・ネットワークを使って算出できるようになります。
2. ベイズフィルタと相関関係
ここではベイズフィルタについて解説します。ベイズフィルタは、ベイジアン・ネットワークとは異なる概念ですが、その理解を深めるための異なる視点を与えてくれます。
そのようなわけで、このページでベイズフィルタについても解説することにします。さっそく見ていきましょう。
2.1. ベイズフィルタとは
ベイズフィルタは、ベイズの定理を一躍有名にした迷惑メールの仕分けに使われている統計的ソフトウェアのことです。これを理解することが、ベイジアン・ネットワークの因果関係の理解にもつながるので、ここで触れておくことにします。
普通、一つのメールの中で使われている一つひとつの単語の間には相関があります。たとえば、メールの中で「出産」や「赤ちゃん」という単語が使われたいたとしたら、両者の間には相関関係があると考えるのが妥当です。
しかし物事を単純化するために、迷惑メールの仕分けにおけるベイズフィルタでは、メールの中に現れる単語は、それぞれ独立事象であると仮定します。単語間の相関関係まで考え始めると、プログラム全体があまりにも複雑になり過ぎて、手に負えなくなるからです。
そこで、あらかじめ存在する相関関係はないと仮定して、反対に、データを蓄積して、その後に相関関係を見出せるようにするという方法をとっています。
これについて、ベイズの定理を使って、より具体的に見ていきましょう。
2.2. ベイズの定理の迷惑メール判定方法
まず以下のように 2 つの事象を定義します。
- \(H_s \cdots\) 迷惑メールである
- \(H_{\overline{s}} \cdots \) 迷惑メールでない
そして、ある単語のリスト \(W_1,\) \(W_2,\) \(\cdots ,\) \(W_n\) があるとします。このとき、それぞれの確率は次のようになります。
- \(P(W_i | H_s)\cdots\cdots\) 迷惑メールである時に単語 \(W_i\) がある確率
- \(P(W_i | H_{\overline{s}}) \cdots\cdots\) 迷惑メールでない時に単語 \(W_i\) がある確率
- \(P(H_s)\cdots\cdots\) メールが迷惑メールである事前確率
- \(P(H_{\overline{s}})\cdots\cdots\) メールが迷惑メールでない確率
さて、受信したあるメールの中の単語が \(W=W_1+W_2+ \cdots + W_n\) だったとします。このとき、この \(W\) を含むメールが迷惑メールかどうかの確率を得るにはどうすれば良いでしょうか。
そう、\(P(H_s|W\) と \(P(H_{\overline{s}}|W\) を比較すれば、そのメールがどのぐらい迷惑メールであるか（これを\(B_f\) とします）の確率を得られます。
具体的には以下のようになります。
\[
\begin{eqnarray}
B_f
&\equiv&
\dfrac
{
P(H_s|W)
}
{
P(H_{\overline{s}}|W)
}
=
\dfrac
{
\dfrac{P(W|H_s)P(H_s)}{P(W)}
}
{
\dfrac{P(W|H_{\overline{s}})P(H_{\overline{s}})}{P(W)}
}\\
&=&
\dfrac
{
P(W|H_s)P(H_s)
}
{
P(W|H_{\overline{s}})P(H_{\overline{s}})
}\\
&=&
\dfrac{P(H_s)}{P(H_{\overline{s}})}
\prod_{i=1}^{n}
\dfrac
{
P(W_i|H_x)
}
{
P(W_i|H_{\overline{s}}
}
\end{eqnarray}
\]
これで \(B_f > 1\) であれば、その度合いによって、どの程度迷惑メールであるかが判断できます。なお、このように定義した \(B_f\) のことを「ベイズ・ファクター」と言います。
さて、このようにして迷惑メールを仕分けるベイズフィルタを作ることができるのですが、事前確率である \(P(H_s)\) と \(P(H_{\overline{s}})\) を定義するのはとても大変です。
しかし、ベイズ統計では、「ベイズ更新」といって新しいデータを得られたときは簡単に上書きできる方法があるので、迷惑メールの精度についてユーザーからデータを集める仕組みを用意しておけば、簡単にアップデートすることができるのです。
こうしたことからも、ベイズの定理またはベイズ統計の優秀さが感じ取れます。
3. まとめ
以上、ものごとの因果関係のネットワークを視覚化したものが、ベイジアン・ネットワークです。非常に重要な数学的技術ですので、しっかりと覚えておくようにしましょう。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント