余事象は、簡単に言うと「ある事象 A に対して、A ではない事象すべて（= A の正反対の事象）」のことです。言葉で表すとこれだけですが、実はこれは現実世界で確率を使いこなせるようになるために、必ずマスターしておくべき概念です。
なぜなら、この余事象という概念から、確率計算において最も重要な法則の 1 つが導き出されているからです。ここでは、その法則についても詳しく解説していきます。
確率論において特に重要なものなので、ぜひしっかりとご覧頂ければと思います。
1. 余事象とは
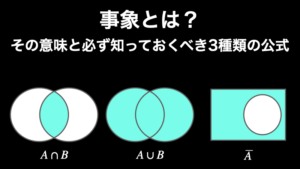
余事象とは、「\(A\) が起こる」という事象 \(A\) に対して、「\(A\) が起こらない」という事象のことです。記号では \(\overline{A}\) または \(A^c\) と表し、ベン図では下図のように表します。
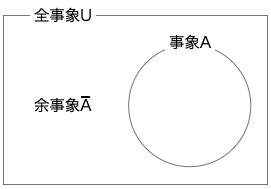
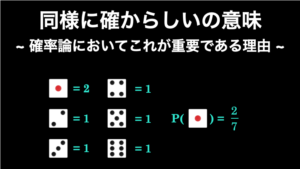
例としてサイコロを振るという試行における余事象を考えてみましょう。この場合、「 1 の目が出る」という事象の余事象は「 1 以外の目が出る」になりますし、「偶数の目が出る」という事象に対する余事象は「奇数の目が出る」になります。
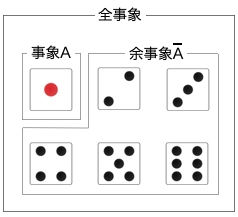
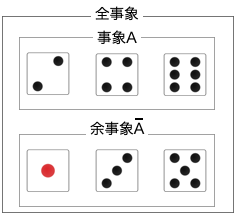
以上が余事象です。
このように事象 \(A\) と余事象 \(\overline{A}\) の関係を視覚的に確認しておくと、余事象の確率の計算方法がとても理解しやすくなります。
2. 余事象の確率の公式
さて、それでは余事象の確率はどのように求められるでしょうか。結論からお伝えすると、以下の公式で求められます。
余事象の確率の公式
\[\begin{eqnarray}
P(\overline{A})
=
1
–
P(A)
\end{eqnarray}\]
たとえば、「 1 の目が出る」という事象の余事象である「 1 の目が出ない」の確率は次のように求められます。
\[\begin{eqnarray}
\text{ 1 の目が出ない確率}
&=&
1
\ –
[\text{ 1 の目が出る確率}]\\
&=&
1-\dfrac{1}{6}\\
&=&
\dfrac{5}{6}
\end{eqnarray}\]
次に「偶数の目が出る」という事象の余事象である「偶数の目が出ない」の確率は次のように求められます。
\[\begin{eqnarray}
\text{ 偶数の目が出ない確率}
&=&
1
\ –
[\text{ 偶数の目が出る確率}]\\
&=&
1-[
\text{ 2 が出る確率}
+
\text{ 4 が出る確率}
+
\text{ 6 が出る確率}
]\\
&=&
1-[\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}]\\
&=&
\dfrac{3}{6}
=
\dfrac{1}{2}
\end{eqnarray}\]
以上が余事象の確率の公式です。これは、とても簡単ですが非常に大事な公式です。なぜ、この簡単な公式がなぜ大事なのかというと、これは確率論において最も重要な公式の一つである「和集合の法則」を導き出すために必要不可欠だからです。
次にこの点について解説します。
3. 余事象と和集合の法則
和集合の法則は、和事象が起こる確率（＝複数の事象のうち少なくとも 1 つ以上が起こる確率）を簡単に導き出すことができる公式です。既に述べた通り、これは確率論の世界でもっとも重要な公式の一つであり、余事象を使って導き出されたものです。
ここでは、この点について解説していきます。確率論の中でも非常に面白いところなので、ぜひ楽しみながら読み進めてください。
なお、ここからは積法定理と加法定理を知っている前提の内容になります。これらについては『事象とは？その意味と必ず知っておくべき 3 種類の公式』で解説していますので、不安な方は、ぜひそちらを先にご覧ください。
それでは見ていきましょう。
3.1. 和集合の法則とは
和集合の法則とは以下の式で表される性質のことです。
和集合の法則
\[\begin{eqnarray}
\text{P(A ∪ B ∪ C ∪} \cdots \text{ ∪ Z)}
=
\
1
\
–
[
\rm{P}(\overline{A})
\times
\rm{P}(\overline{B})
\times
\rm{P}(\overline{C})
\times
\cdots
\times
\rm{P}(\overline{Z})
]
\end{eqnarray}\]
文字で伝えるなら、「A または B または C が起こる確率（それぞれが同時に起こる場合も含む）は、それぞれの事象の余事象の確率の積を１から引いたものと等しい」ということです。
それでは実際に、この和集合の法則を使って確率を求める例を見ることで、この法則の重要性をしっかりと頭に入れていきましょう。
3.2. 和集合の法則の実例
例として次のような問題があるとします。
ある営業マンが、今週 1 週間に 5 社の顧客と商談のアポイントメントが取れているとします。そして今までの記録から、この営業マンは 1 つの商談の成約率が 20 % であることがわかっています。営業マネージャーであるあなたは、今週の目標達成の進捗管理のために、それぞれの営業マンの成約数の予測を行う必要があります。さて、あなたは、この営業マンが今週に最低 1 社以上と成約する確率をどのように見積もるべきでしょうか。
少し考えてみてください。
いかがでしょうか。答えは「成約率の 20% が 5 社なのだから 100 % です…」ということにはもちろんなりません。確率論に不慣れな方はこのように考えてしまいますが、それは大きな勘違いです。
この問題は、和集合の法則を使って解くべき問題の典型例です。
まず「A 社が成約」「B 社が成約」「C 社が成約」「D 社が成約」「E 社が成約」を、それぞれ事象 \(A, B, C, D, E\) とします。そうすると、最低 1 社以上成約するというのは、これらの和事象 \(A \cup B \cup C \cup D \cup E\) が起こるということです。
勘の良い方は、この時点で、なぜ最低 1 社以上成約する可能性が 0.2 + 0.2 + 0.2 + 0.2 + 0.2 = 1 にならないのかわかると思います。この計算では、たとえば「 A と B がともに成約する場合」というように、複数社が同時に成約する場合の確率が二重に足されていることになってしまうのです（詳しくは「加法定理」をご確認ください）。
しかし、いちいち全てのケースの和事象の確率を計算するのはとても手間です。そこで発想を転換してみましょう。そうすると、「最低 1 社以上成約する」場合というのは、「A,B,C,D,E 社の全てと同時に成約しない」場合の正反対であるということに行き着きます。
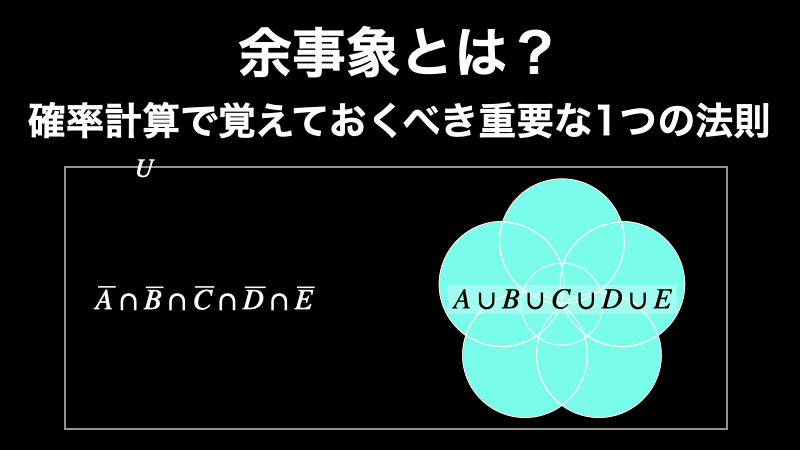
つまり \(≈\) が起こる場合というのは、それぞれの余事象の積事象 \(\overline{A} \cap \overline{B} \cap \overline{C} \cap \overline{D} \cap \overline{E}\) が起こらない場合であるということなのです。
以下のベン図を見てみるとわかりやすくなると思います。
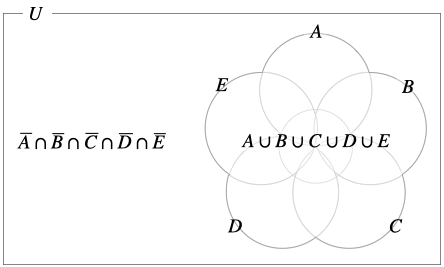
以上のことから、今週、この営業マンが 1 社以上成約する確率は、積法定理を使って、以下のように求められます。
\[\begin{eqnarray}
P(A \cup B \cup C \cup D \cup E)
&=&
1-P(\overline{A} \cap \overline{B} \cap \overline{C} \cap \overline{D} \cap \overline{E})\\
&=&
1 –
[
P(\overline{A})
\times
P(\overline{B})
\times
P(\overline{C})
\times
P(\overline{D})
\times
P(\overline{E})
]\\
&=&
1-
[0.8 \times 0.8 \times 0.8 \times 0.8 \times 0.8]\\
&=&
0.67
\end{eqnarray}\]
このように実際は 67 % しかないのですね。それにも関わらず 100 % と見積もってしまうようでは営業マネージャーとしての職を追われてしまうことになりかねません。
以上は余事象の重要性を示す確率論の話のほんの一部に過ぎません。このような実生活の役に立つ確率の話は『確率とは？人生で得するために必ず知っておきたい７つのこと』でまとめているので、ぜひご覧頂ければと思います。
3.3. 和集合の法則の証明
ここまで見てきたように和集合の法則とは、和事象が起こる確率（＝複数の事象のうち少なくとも 1 つ以上が起こる確率）を簡単に導き出すことができる公式です。このことは先ほどのベン図を見て頂ければ、わかることではありますが、ここでは改めて数式から導き出してみましょう。
なお、説明の仕方は異なりますが、『集合とは？覚えておくべき 6 つの記号と 1 つの法則』で解説しているド・モルガンの法則と全く同じなので、両方確認してみると良いでしょう。
それでは始めます。
まず 2 つの独立事象 A と B と、その余事象について考えてみましょう。
A か B の少なくとも一方の事象が起こった場合というのは、2 つの余事象 \(\overline{A}\) と \(\overline{B}\) の両方が起こったケースではないということは明らかです。
たとえばトランプを 1 枚引いて 〈エースを引く〉という場合を事象 A 、〈ダイヤを引く〉という場合を事象 B としましょう。このとき \(\overline{A}\) は〈エース以外を引く〉で、\(\overline{B}\) は〈ダイヤ以外を引く〉という場合のことになります。
そして、この場合、A か B の少なくとも一方が起こる（= \(A \cup B\)）というのは、〈エースを引くか、ダイヤを引くか、もしくは両方を引く〉というが起こるということです。そして、これが起こったときは、当然、\(\overline{A}\) と \(\overline{B}\) が同時に起こったケース \(\overline{A} \cap \overline{B}\) ではないということになります。
ということは、これを反対から見ると、 〈A か B の少なくとも一方が起こった〉ということは〈\(\overline{A}\) と \(\overline{B}\) の余事象が同時に起こった〉と等しいということになります。
以上のことから、余事象の定義より次の式を書くことができます。
\[\begin{eqnarray}
\rm{P(A \cup B)} = 1 \ – [\rm{P(\overline{A} \cap \ \overline{B})}]
\end{eqnarray}\]
次に事象 A と B が互いに独立しているということは、その余事象 \overline{A} と \overline{B} も互いに独立しているということを意味します。そして、確率の乗法定理より、2 つの独立事象が同時に起こる確率は、個々の独立事象が起こる確率の積に等しくなります。
以上のことから、上の式は以下のように書き換えることができます。
\[\begin{eqnarray}
\rm{P(A \cup B)} = 1 \ – \rm{P(\overline{A})} \times \rm{P(\overline{B})}
\end{eqnarray}\]
この法則は、事象の数にかかわらず通用します。そのため、たとえば独立事象 Aか B か C か D が起こる確率（＝ A, B, C, D のいずれか 1 つが起こる可能性 + いずれか 2 つが起こる可能性 + いずれか 3 つが起こる可能性 + 4 つすべてが起こる可能性）は、以下の式で求められることになります。
\[\begin{eqnarray}
&& \rm{P(A \cup B \cup C \cup D)}
&=& 1 \ – [ \rm{P(\overline{A})} \times \rm{P(\overline{B})} \times \rm{P(\overline{C})} \times \rm{P(\overline{D})} ]
\end{eqnarray}\]
以上が証明です。
4. まとめ
最後までご覧いただきありがとうございます。ぜひ、ここで解説した余事象の内容はしっかり覚えておくようにしてください。
重要な点を改めてまとめると以下の通りです。
- 余事象は 「A が起こる」という事象に対して、その正反対の「 A が起こらない」という事象である
- ある事象を \(A\) 、その余事象を \(\overline{A}\) とすると、\(P(\overline{A})=1-P(A)\) となる
- 事象の数に関わらず、和事象 \(A \cup B \cup C\) の確率は、\(P(A \cup B \cup C) = 1- P(\overline{A} \cap \overline{B} \cap \overline{C}) = 1- [P(\overline{A}) \times P(\overline{B}) \times P(\overline{C})]
\) で求められる
ぜひお役に立てて頂ければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント