集合とは、簡単に言うと「何らかのモノが集まっているもの」のことです。これは集合論や確率論・論理学だけでなく、ほぼすべての数学分野で、非常によく使われます。なぜなら集合は、「数学の様々な演算をわかりやすく、やりやすくしてくれる非常に便利なツール」だからです。
そこで、このページでは、この集合について、様々な分野に応用できるように、かつ柔軟に理解できるようにわかりやすく解説していきます。集合は、一見すると、とても簡単なものに見えますが、実はとても奥深く重要なものです。
ぜひ参考にして頂ければ嬉しく思います。
1. 集合とは
集合とは、冒頭で述べた通り、「何らかの “もの” の “集まり”」 のことです。そして集合を構成する個々の “もの” のことを「要素」と言います。集合の要素は、数字・食べ物・記号などなど、それが誰から見ても区別可能なものであるなら何でも構いません。
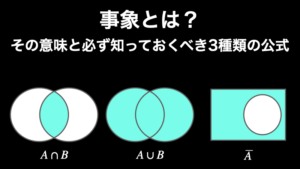
集合を示すときには、視覚的なわかりやすさから、以下のようなベン図がよく使われます。
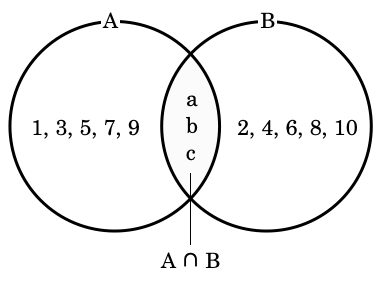
1.1. 集合の表記方法
集合を表記するときは、要素を波括弧 { } で囲んで表す決まりになっています。
たとえばトランプのスート全体の集合は \( \{ \clubsuit, \diamondsuit, \heartsuit, \spadesuit \} \) と表しますし、トランプの数字全体の集合は \( \{\rm{A},2,3,4,5,6,7,8,9,10,\rm{J,Q,K} \}\) と表します。誰かの好きな食べ物の集合なら \( \{ \)寿司, ラザニア, ピザ\( \} \) と表します。
通常は、それぞれの集合を区別するために A や B などの名前をつけるのが一般的です。たとえば 1 以上 10 以下の偶数全体の集合を A、奇数全体の集合を B とするなら、次のように書きます。
A = { 2, 4, 6, 8, 10 }
B = { 1, 3, 5, 7, 9 }
要素の数が多くて、いちいち全てを書き並べるのが面倒な場合は、以下のように条件式で表すことも可能です。
A = { x | x は 1 以上 10 以下の偶数 }
B = { x | x は 1 以上 10 以下の偶数 }
このように要素を条件式で表すことを「内包 “intension”」と言います。この言葉を覚えなければいけないわけではありませんが、プログラミング学習時に「リスト内包表記」などのテクニックが出てきたりするので、そうした場合に早く理解できるというメリットがあります。
1.2. 属する・属さない(∈ と ∉)
さて、上の集合 A の中に 2 という要素は存在します。このことを「2 は集合 A に属する」と言います。反対に、集合 A の中に 1 という要素は存在しません。このことを「1 は集合 A に属さない」と言います。
これらは帰属記号 ∈ と、非帰属記号 ∉ 使って次のように表すことができます。
2 ∈ A
1 ∉ A
集合論ではたくさんの記号が出てきますが、これらの記号はもっとも基本となるものです。
1.3. 空集合は Φ
なお要素が存在しない集合を扱う場合もあります。そのような集合を「空集合」と言い、記号の Φ で表します。
Φ = { }
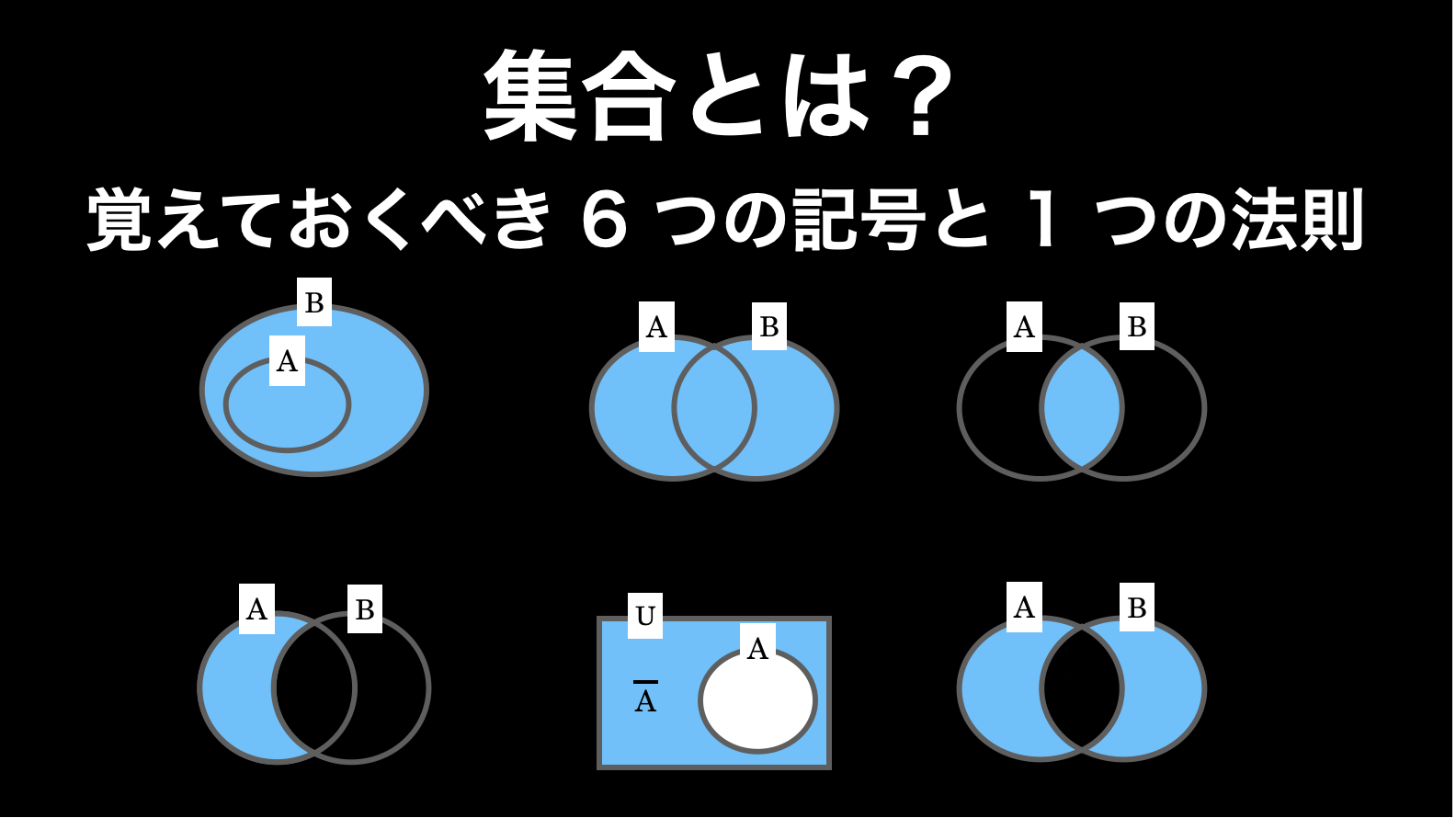
2. 必須の集合記号 6 つ
集合論では、さまざまな集合を記号を使って表すことができます。中でも以下の 6 つは基本です。
部分集合:A ⊂ B
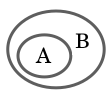
集合 A の要素が全て集合 B にも属するとき、「A は B の部分集合である」という。
例:{ 1, 2 } ⊂ { 1, 2, 3}
和集合:A ∪ B
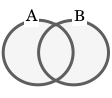
集合 A と B の少なくとも一方に属する要素全体を「A と B の和集合」という。
例:{ 1, 2 } ∪ { 3 } = { 1, 2, 3 }
共通部分:A ∩ B
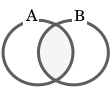
集合 A と B のどちらにも属する要素全体を「A と B の共通部分」という。
例:{ 1, 2, 3 } ∩ { 2, 3, 4} = { 2, 3 }
差集合:A \ B
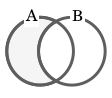
集合 A から集合 B を差し引いた要素全体を「A と B の差集合」という。
例:{ 1, 2, 3 } \ { 2, 3 } = { 1 }
補集合:\(\overline{A}\)
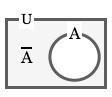
全体集合 U があるとき、集合 A 以外の要素を「A の補集合」という。
例:U = { 1, 2, 3 }, A = { 1 }, \(\overline{A}\)= { 2, 3 }
対称差:A △ B
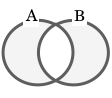
“A に属しB に属さない要素”と”B に属しA に属さない要素”の全体を「A と B の対称差」という。
例:{ 1, 2, 3 } △ { 2, 3, 4 } = { 1, 4 }
最初は覚えるのが面倒に感じるかもしれませんが、これらの記号を使いこなせるようになると、数学の様々な分野において、学習や計算がスムーズになり非常に便利です。繰り返し確認して一つずつ暗記していきましょう。
3. ド・モルガンの法則
集合記号を押さえたら必ず覚えておきたい法則があります。それは「ド・モルガンの法則」です。なぜなら、この法則を知っておけば、ほとんどありとあらゆる集合を記号で表せるようになる(=結果、計算が楽になる)からです。
ド・モルガンの法則は、上で見た集合記号の中でも、和集合・共通部分・補集合の 3 つの間に成り立つ以下の規則性です。その規則性とは以下のものです。
\[
(1) \overline{A \cup B}=\overline{A} \cap \overline{B}\\
(2) \overline{A \cap B}=\overline{A} \cup \overline{B}
\]
これらはそれぞれ言葉で表すと 、「”A と B の和集合”の補集合は、A の補集合と B の補集合の共通部分と等しい」、「”A と B の共通部分” の補集合は、A の補集合と B の補集合の和集合と等しい 」ということです。
ベン図で表すと以下の通りです。
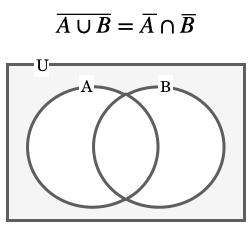
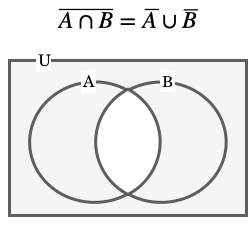
この「ド・モルガンの法則」は集合を扱う時には、ほとんど必ず目にするので覚えておきましょう。
4. 集合の練習問題
さて、ここまでで集合の基本はすべて解説しました。最後に、解説してきた知識を使って実際に問題を解いてみましょう。ここの問題を理解すると、これから集合を使いこなすための土台をしっかりと築けたということです。
それでは見ていきましょう。
練習問題 ①
全体集合 U に 1 以上 100 以下のすべての自然数があるとします。この U の中に、3 の倍数を要素とする集合 A、7 の倍数を要素とする集合 B があります。集合 A は {3, 6, …, 96, 99} なので、要素の数は 33 個あります。集合 B は {7, 14, …, 91, 98} なので、要素の数は 14 個あります。これを n(A) = 33、n(B) = 14 というように表します。
これらの集合を使って、3 の倍数または 7 の倍数を全要素とする集合を記号で示し、その要素の数を求めてください。
集合の問題は、実際にベン図を描いて考えるのが定番です。ベン図を描くと、” 3 または 7 の倍数の集合 ” は、集合 A と B の和集合 A ∪ B であることが、すぐにわかります。
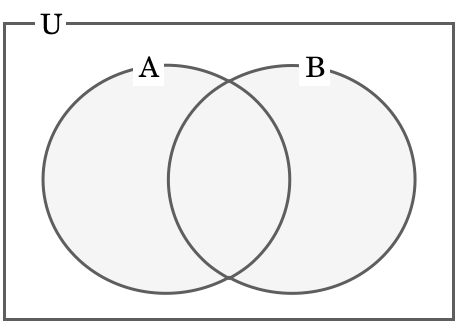
それでは、この和集合 A ∪ B の要素の数はどのように求められるでしょうか。
ついつい A + B で求められると考えてしまいそうですが、そうではありません。A + B だと、共通部分 A ∩ B が 重複して足されていることになるからです。そのため、A ∪ B を求めるには A + B – A ∩ B を行う必要があります。
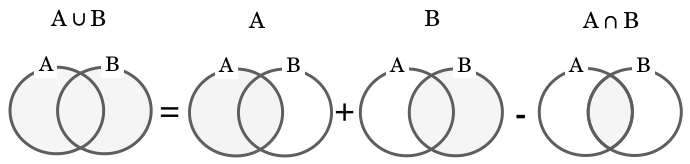
さて、ここで共通部分 A ∩ B は 3 の倍数と 7 の倍数の共通部分なので、最小公倍数である 21 の倍数となることがわかります。このことから A ∩ B = {21, 42, 63, 84} なので n(A ∩ B) = 4 になります。
以上のことから解答は次の通りです。
問題 ① の解答
- 集合記号:A ∪ B = A + B – A ∩ B
- 要素の数:n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 33 + 14 – 4 = 43
練習問題 ②
引き続き、全体集合 U と集合 A、B があるとき、3 で割り切れない数を全要素とする集合を記号で示し、その要素の数を示してください。
3 で割り切れない数の集合は、ベン図で次のように描けます。
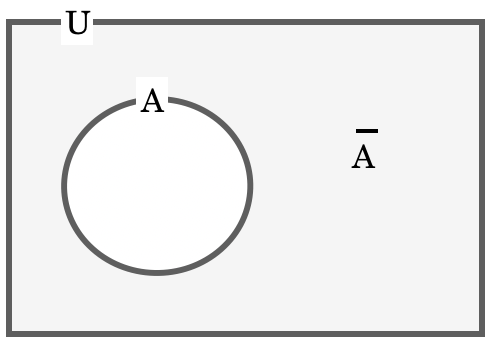
この図を見ると、3 で割り切れない数の集合とは、3 の倍数の集合 A の補集合 \(\overline{A}\) であるということがわかります。そして全体集合 U の数は n(U) = 100 なので、解答は以下の通りになります。
問題 ② の解答
- 集合記号:\(\overline{A}\) = U – A
- 要素の数:n(\(\overline{A}\)) = n(U) – n(A) = 100 – 33 = 67
練習問題 ③
引き続き、全体集合 U と集合 A、B があるとき、3 でも 7 でも割り切れない数を全要素とする集合を記号で示し、その要素の数を示してください。
3 でも 7 でも割り切れない数は、ベン図を描くと次のようになります。
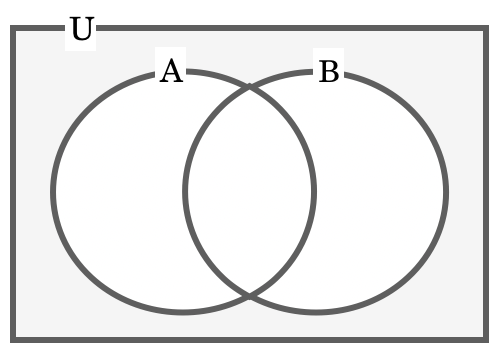
こうやって描いてみると、ド・モルガンの法則の \(\overline{A \cup B}\) の形になっていることがわかります。同時に、これは U – A ∪ B で求められることもわかります。
以上のことから解答は次の通りになります。
問題 ③ の解答
- 集合記号:\(\overline{A \cup B}\) = U – A ∪ B
- 要素の数:n(\(\overline{A \cup B}\)) = n(U) – n(A ∪ B) = 100 – 43 = 57
練習問題 ④
引き続き、全体集合 U と集合 A、B があるとき、3 では割り切れて 7 では割り切れない数を全要素とする集合を記号で示し、その要素の数を示してください。
3 では割り切れて 7 では割り切れない数は、ベン図を描くと次のようになります。
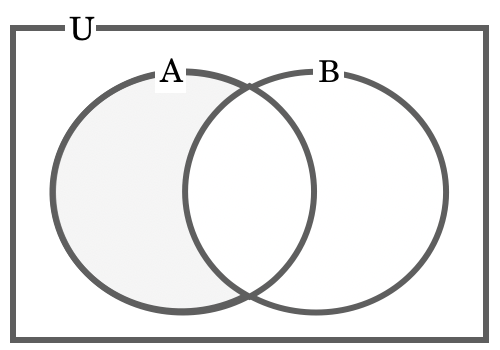
こうして見ると、これは差集合 A \ B (もしくは A ∩ \(\overline{B}\) でも良い)であることがわかります。そして、これは A – A ∩ B で求められることもわかります。
以上のことから解答は次の通りになります。
問題 ④の解答
- 集合記号:A \ B = A – A ∩ B
- 要素の数:n(A \ B)= N(A) – n(A ∩ B) = 33- 4 = 29
5. まとめ
以上が集合です。
最初は記号に慣れるのが大変に感じるかもしれませんが、練習問題を解いたり、日常的に集合に触れているうちに勝手に覚えていることでしょう。そして集合の知識が真価を発揮するのは、数学の応用分野に進んだときです。どのような応用分野でも集合はほとんど必ず使うことになるからです。
そのためぜひ、しっかりと理解するようにしておきましょう。


コメント