同様に確からしいの意味を誰でも理解できるようにわかりやすく解説

「同様に確からしい」とは、ある試行において起こりうる事象のすべてが「同じように起こる可能性があると考えられる」という意味です。たとえばコイントスでは、表の方が裏よりも出やすいということはなく、表が出る可能性と裏が出る可能性は同じであると期待できます。このとき「表が出る事象と裏が出る事象は同様に確からしい」と言います。

これは確率を計算するときの前提であり、これがなければ確率を議論することはできなくなるため、とても重要な概念です。

このページでは、この「同様に確からしい」ということの意味について、もう少し踏み込んで解説します。なお内容をしっかり理解するためには、以下の用語の意味をおさらいしておくことが役立ちます。

それでは始めましょう。

1. 同様に確からしいとは

「同様に確からしい」は、英語では “equally probable” であり、直訳すると「同じ様にありそう・・・・」という意味です。

たとえば、コイントスをしたら、表が出ることも、裏が出ることも同様にありそうです。サイコロを振ったら、1 の目が出ることも、2 の目が出ることも、3 の目が出ることも、4 の目が出ることも、5 の目が出ることも、6 の目が出ることも「同じ様にありそう」です。そのため、これらの試行において、それぞれの根元事象は「同様に確からしい」ということになります。

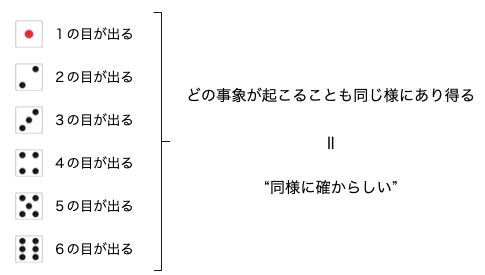
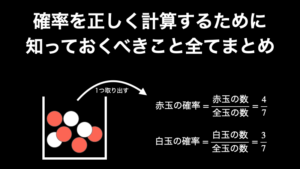
以上のことから、サイコロ振りにおける根元事象の確立は、それぞれ 1 / 6 = 16.67% と導き出すことができます（確率の計算方法は『確率の求め方（計算方法）と最低限知っておくべき2つの公式』で解説しています）。

さて、ここまで見てきて「同様に確からしい」ということに、なんとなく気持ち悪さを感じた方もいるかもしれません。それは、これが公式や法則というわけではなく、あくまでも確率を求めるための単なる人工的な取り決めに過ぎないからです。

例えば、重心の偏りが全くない理想的なサイコロの場合、確かにそれぞれの目が出るという事象は「同様に確からしい」でしょう。しかし現実的には、そのような完璧なサイコロはありません。そのため確率には、日常的には問題にならないほどの小さなものではありますが、ズレが入り込む余地があります。

それでも「同様に確からしい」という取り決めを置くのは、そもそもそうしなければ確率について議論することができないからです。厳密性を重要視する数学において、確率論だけは、このような野蛮なところがあるという点でとても特殊な地位にあるのです。

もちろん、だからと言って確率論や、そこから派生する統計学が役立たずということにはなりません。それどころか、まったく正反対で、近年、機械学習や AI という手法が日の目を浴びるようになって、これらの学問の重要性はますます大きくなっています。

ある意味で数学の中で最も不確実な分野である確率論が、科学技術の進歩の大きな部分を占めるようになっているのは、とても興味深いことですね。量子論と似たものがあるように思います。

2. 同様に確からしくない場合

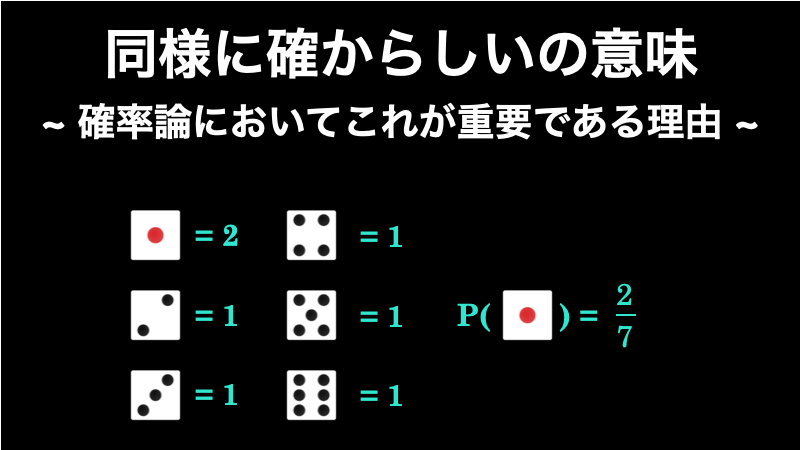
さて、それでは「同様に確からしくない」場合はどうすれば良いでしょうか。たとえば、1 の目が出やすいように重心にイカサマが仕掛けられたサイコロのような場合です。この場合は、もちろん 1 の目が出る確率と、その他の目が出る確率は異なります。

このような場合は「重み付け」という操作を行います。

たとえば、このイカサマサイコロでは 1 の目が他の目と比べて 2 倍出やすくなっているとします。その場合は、それぞれの目を下図のように重み付けして、確率を計算します。

重要なのは、このような重み付けの操作も、「同様に確からしい」という取り決めがあるからこそ可能になるということです。この取り決めがなければ、そもそも、特定の根元事象が起こりうる可能性を n 倍するという操作ができないからです。

つまり結局、ある試行における根元事象が同様に確からしい場合と、確からしくない場合のいずれにおいても、確率計算の根底には「同様に確からしい」の取り決めがあるということです。冒頭で、「同様に確からしい」の取り決めがなければ確率を議論することはできなくなるとお伝えしましたが、それはこういう意味です。

3. まとめ

以上が「同様に確からしい」の意味です。一見すると、なんだか意味がわかりにくい言葉ですが、実は確率論について議論するための必要不可欠な取り決めなのですね。だからこそ、確率について学ぶときに最初に教わる概念になっています。

少しでも理解の足しになったなら嬉しく思います。