円順列とは？解き方の公式と覚えるべき4つのパターン

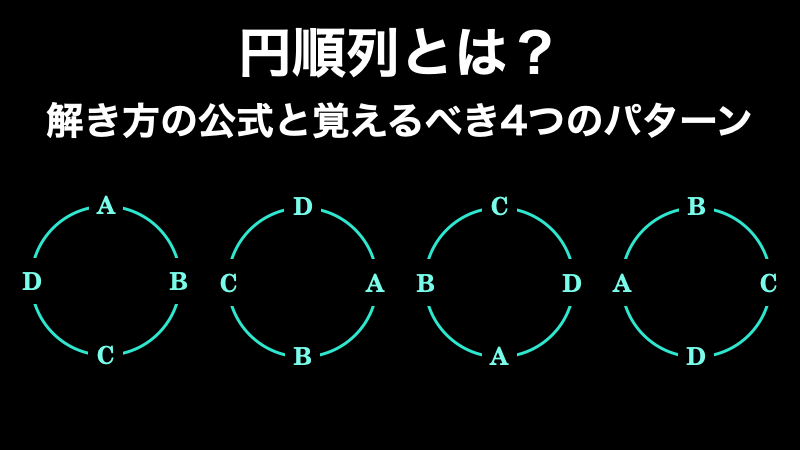
円順列は、文字通り、要素を円形に並べたもののことです。通常の順列とは異なって円形であるため、回転した場合に同じ並びになるものは 1 通りとして考えます。なお通常の順列は『順列とは？抑えておきたい3つの公式と計算方法』で解説しています。

当ページでは、この円順列の解き方の公式と、この公式で円順列が求められる理由を解説します。そして、その後に頻出する 4 つのパターンに関しての練習問題を用意しています。円順列は当ページの内容を理解していればバッチリ応用もきくようになるので、ぜひ参考にして頂ければと思います。

1. 円順列とは

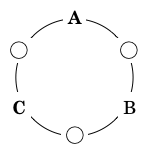
円順列とは、要素を円形に並べたもののことです。円順列は、以下に示しているように、同じ並び順（この場合は時計回りに ABCD の並び）が回転しただけのものは同一の順列と考え、1 通りと数えます。

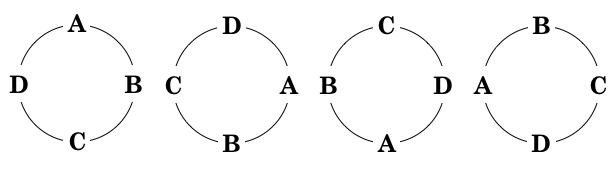
そのため、このような A, B, C, D の円順列の「場合の数」は、通常の順列のように 4! = 24 通りではなく、{ABCD, ABDC, ACBD, ACDB, ADBC, ADCB} の 6 通りになります。

それでは次に円順列の求め方について見ていきましょう。

2. 円順列の公式

円順列は以下の公式で簡単に求めることができます。

たとえば 4 つの要素の円順列は \((4-1)! = 3 \times 2 \times 1 = 6\) 通りですし、5 つの要素の円順列は \((5-1)! = 4 \times 3 \times 2 \times 1 = 24\) 通りです。

それでは、なぜ、この公式で求められるのでしょうか。考え方は 2 つあります。

• 通常の順列を算出して要素数で割る
• 要素を 1 つ固定すると考える

それぞれ見ていきましょう。

通常の順列を算出して要素数で割る

まず、n 個の要素を円順列で並べる場合、同じ並び順を回転させただけのものは必ず n 通り現れます。

例として、上でも出てきた　A, B, C, D の 4 つの要素の円順列について考えてみましょう。A, B, C, D の 4 つの要素から 4 つを取り出して並べる場合の通常の順列は、\({}_4P_4=4 \times 3 \times 2 \times 1 = 24\) 通りです。しかし上で見たように、この円順列は、回転すると同じ並びになるものが 1 組 4 個存在することがわかっています。

そのため、この円順列は以下の通り求められることがわかります。

以上より、n 個の異なる要素の円順列は (n-1)! となります。

要素を 1 つを固定すると考える

もう一つのパターンは、ある 1 つの要素の位置を固定して考えるというものです。たとえば A を上に固定すると考えてみましょう。固定する場所はどこでも構いません。なぜなら、どこに固定したとしてもすべて同じ並びの同一の順列になるからです。

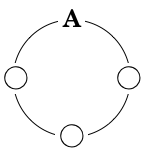
こうすると結局、残った 3 つの異なる要素を並べた場合の順列を求めることと同じになります。そのため \({}_3P_3=3!=3 \times 2 \times 1 = 6\) と求められます。樹形図で確認してみると次の通りです。

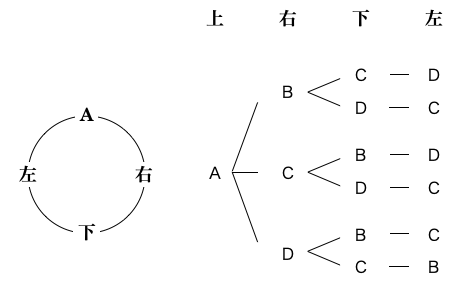
以上より、やはり n 個の異なる要素の円順列は (n-1)! になります。

3. 円順列の問題

それでは、ここからは理解を深めるために実際に練習問題を解いてみましょう。

問題① 簡単な円順列

これは簡単です。単純に要素が 6 つの円順列なので以下の通り求められます。

問題② 特定の要素が向かい合う円順列

これは次のように要素を 2 つ固定した順列であると考えられます。

そのため単純に残った 4 つの要素を並べる問題になるので、回答は次の通りになります。

問題③ 特定の要素が交互の円順列

これは以下のように 3 つの要素を固定した順列と同じです。

そのため 3 つの要素の並べる問題と同じになります。

問題④ じゅず順列

これは \((4-1)!=6\) 通りと答えてしまいそうですが、そうではありません。リングなので、以下に示している通り、裏返すと同じになる左右対称のパターンは同一のものになるのです。

そのため正解は次のようになります。

このようにじゅず順列の場合は、2 で割る必要がありますので覚えておきましょう。

4. まとめ

ここまで解説してきたように円順列は、とても簡単なものです。しかし単に公式を暗記するというだけではなく、「なぜそうなるのか？」という点をしっかりと理解しておくことが重要です。そうして初めて、さまざまな数学分野に応用が効くようになるからです。