「ブロードキャスト」とは、NumPyの配列の算術演算の時に、shapeの異なる配列を扱う上での作法です。これを知っておくことによって、shapeの異なる配列同士の演算が非常に楽になりますし、ほとんどの場合、処理の面でも高速になります。
ここでは、このブロードキャストについて詳しく解説していきます。
1. ブロードキャストとは
NumPyの配列同士の演算を行う時は、基本的には以下のコードのように、2つの配列のshapeは全く同じである必要があります。
>>> from numpy import array
>>> a = array([1.0, 2.0, 3.0])
>>> b = array([2.0, 2.0, 2.0])
>>> a * b
array([ 2., 4., 6.])
ブロードキャストは、この「演算処理を行う2つの配列同士のshapeが揃っていなければならない」という制限を緩めてくれるものです。最もシンプルなブロードキャストは、以下のコードのように、配列とスカラー(要素が1つの数値)の演算でしょう。
>>> from numpy import array
>>> a = array([1.0,2.0,3.0])
>>> b = 2.0
>>> a * b
array([ 2., 4., 6.])
この演算結果は、 b に a と同じshapeの配列を渡した先ほどのコードと同じです。
これは、下図のように、演算の間はスカラー b が配列 aと同じshapeに伸長されて処理が行われているということです。

これがブロードキャストです。
2つ目のコードの方が、1つ目のコードよりも効率的です。なぜなら、2つ目のコードでは、 bは配列ではなくスカラーなので、単純に消費するメモリーが少量で済むからです。
2. ブロードキャストのルール
ブロードキャストのルールは以下の2つです。
- 同じ次元数の配列同士の演算の場合、一方の配列のshapeのうち1つが
1でそれ以外は同じである時にブロードキャストが行われる。 - 次元数が異なる配列同士の演算の場合、「後端の軸」が一致しているか、「一方の配列の後端の軸の1つが
1」である時にブロードキャストが行われる。
どちらの場合も、演算結果の配列のshapeは 1を含んでいない方になります。
このルールを満たさない場合は、ValueError: operands could not be broadcast togetherというメッセージが表示されます。
それぞれ見ていきましょう。
2.1. 同じ次元数の配列同士の演算の場合
同じ次元数の配列同士の演算の場合、一方の配列のshapeのうち1つが 1 でそれ以外は同じである時にブロードキャストが行われます。
実際に見てみましょう。
''' 2次元配列同士の演算は、一方の配列のshapeのうち
1つが1でそれ以外は同じ場合、ブロードキャスト '''
>>> import numpy as np
# shape(3,1)の配列を作成
>>> a = np.arange(3).reshape(3,1)
>>> a
array([[0],
[1],
[2]])
# shape(3,3)の配列を作成
>>> b = np.arange(9).reshape(3, 3)**2
>>> b
array([[ 0, 1, 4],
[ 9, 16, 25],
[36, 49, 64]])
# shape(3,1) * shape(3,3)
>>> a * b
array([[ 0, 0, 0],
[ 9, 16, 25],
[ 72, 98, 128]])
これはshape(3, 3)の配列 aとshape(3, 1)の配列 bの演算です。「一方の配列のshapeのうち1つが 1で、それ以外は同じ」というルールに則っているのでブロードキャストして演算が実行されます。
条件を満たす場合、演算結果は 1を含んでいない方のshapeになります。
2.2. 次元数が異なる配列の演算の場合
次元数が異なる配列同士の演算の場合は、「後続の軸」が一致しているか、「一方の配列の後続の軸の1つが 1」である場合にブロードキャストが行われます。それ以外の場合はエラーになります。
「後続の軸」とは何でしょうか。例えば一方の配列が shape(1,2,3)で、もう一方がshape(2,3)だとします。この場合、「後端の軸」は後ろの 2x3 の次元のことを指します。shape(5, 4, 3, 2)とshape(3, 2)の配列同士の演算の場合は、後端の軸は後ろの 3x2 の次元のことを指します。shape(5, 4, 3, 2)とshape(4, 3, 2)なら、後ろの 4x3x2 の次元が後端の軸になります。
繰り返しになりますが、次元数が異なる配列の場合、この「後端の軸」が一致しているか、一方の配列の後端の軸の1つが 1である場合にブロードキャストが行われます。
実際のコードで確認してみましょう。
''' 次元数が異なる配列同士の演算は、
①「後続の軸」が一致している、または
②どちらか一方の「後続の軸」の1つが 1
の場合にブロードキャスト '''
# 2 x 2 x 3 の3次元配列
>>> a = np.arange(10, 22).reshape(2, 2, 3)
>>> a
array([[[10, 11, 12],
[13, 14, 15]],
[[16, 17, 18],
[19, 20, 21]]])
# 2 x 3 の2次元配列
>>> b = np.arange(6).reshape(2, 3) * 0.1
>>> b
array([[0. , 0.1, 0.2],
[0.3, 0.4, 0.5]])
# 2 x 1 の2次元配列
>>> c = np.arange(1, 3).reshape(2, 1) * 0.1
>>> c
array([[0.1],
[0.2]])
# shape(2,2,3)の配列 aと shape(2,3)の配列 bの演算
>>> a * b
array([[[ 0. , 1.1, 2.4],
[ 3.9, 5.6, 7.5]],
[[ 0. , 1.7, 3.6],
[ 5.7, 8. , 10.5]]])
# shape(2,2,3)の配列 aと shape(2,1)の配列 cの演算
>>> a * c
array([[[1. , 1.1, 1.2],
[2.6, 2.8, 3. ]],
[[1.6, 1.7, 1.8],
[3.8, 4. , 4.2]]])
まず、配列 aと bの演算は shape(2,2,3)と shape(2,3)の演算です。この場合、後端の軸は 2x3 で一致しているのでブロードキャストが行われます。
次に、配列 aと cの演算はshape(2,2,3)と shape(2,1)の演算です。この場合、後端の軸は一致していませんが、一方の軸の1つが 1なのでブロードキャストが行われます。
以上がNumPyの配列のブロードキャストのルールです。
3. サンプルコード
他にもいくつか見てみましょう。
例えば、以下のような配列同士の演算の場合は、「後端の軸」は 1x6x1 と 7x1x5 です。これらのうち、 1の方の軸が、長い方の配列の軸の長さに合わせてブロードキャストします。
A (4d array): 8 x 1 x 6 x 1
B (3d array): 7 x 1 x 5
Result (4d array): 8 x 7 x 6 x 5
以下の例も確認しておきましょう。
A (2次元配列): 5 x 4
B (1次元配列): 1
Result (2次元配列): 5 x 4
A (2次元配列): 5 x 4
B (1次元配列): 4
Result (2次元配列): 5 x 4
A (3次元配列): 15 x 3 x 5
B (2次元配列): 3 x 5
Result (3次元配列): 15 x 3 x 5
A (3次元配列): 15 x 3 x 5
B (2次元配列): 3 x 1
Result (3次元配列): 15 x 3 x 5
以下は、ブロードキャストしない例です。
A (1次元配列): 3
B (1次元配列): 4 # 「後続の軸」が一致しない
A (2次元配列): 2 x 1
B (3次元配列): 8 x 4 x 3 # 後ろから2つ目の軸が一致しない
実際のコードも見ておきましょう。
>>> x = np.arange(4) #shape(4,)
>>> xx = x.reshape(4,1) #shape(4, 1)
>>> y = np.ones(5) #shape(5,)
>>> z = np.ones((3,4)) #shape(3, 4)
>>> x + y
ValueError: operands could not be broadcast together with shapes (4,) (5,)
>>> xx + y
array([[ 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3.],
[ 4., 4., 4., 4., 4.]])
>>> (xx + y).shape
(4, 5)
>>> x + z
array([[ 1., 2., 3., 4.],
[ 1., 2., 3., 4.],
[ 1., 2., 3., 4.]])
>>> (x + z).shape
(3, 4)
ブロードキャストは、外積などの演算を簡単にしてくれます。以下のコードでは、例として、2つの1次元配列の外和の演算を行っています。
>>> a = np.array([0.0, 10.0, 20.0, 30.0])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a[:, np.newaxis] + b
array([[ 1., 2., 3.],
[ 11., 12., 13.],
[ 21., 22., 23.],
[ 31., 32., 33.]])
ここで使っている newaxis は配列 aに新しい軸を足して、4x1 の2次元配列にしています。4x1 の配列をshape(3,) の bと組み合わせることで、4x3 の配列を生成しています。
4. ブロードキャストの応用
ブロードキャストは、実世界の問題においてよく使われます。典型的な例は、情報理論や分類などに使われるベクトル量子化アルゴリズムでしょう。
ベクトル量子化アルゴリズムの基本的な操作は、ポイントのセットの中から最近ポイントを見つけるというものです。
最も単純な例としては以下のような2次元のケースがあります。値は、分類を行うスポーツ選手の身長と体重を示しています。そして、コード(グレー丸)は異なるスポーツ選手のクラスを表しています。黒四角への最近ポイントを見つけるには、各データ(身長と体重)とそれぞれのコードの間の距離を計算する必要があります。この例では、黒四角のスポーツ選手は、バスケットボール選手に最も近いことがわかります。
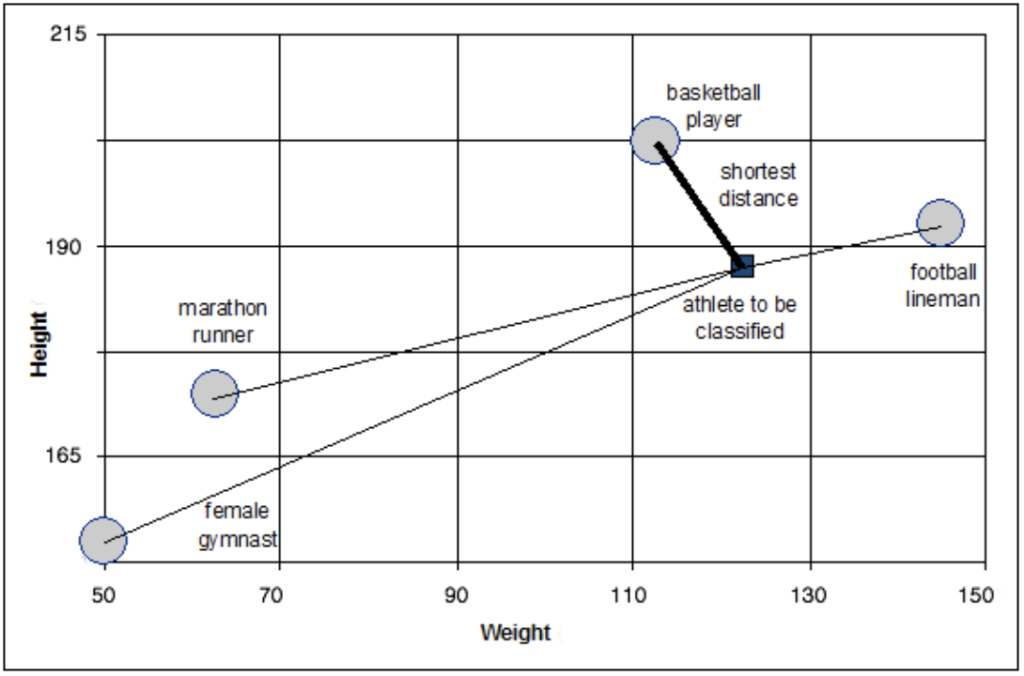
出典:Array Broadcasting in Numpy
5. まとめ
以上がNumPyの配列のブロードキャストのルールです。覚えておくと便利なので、ぜひ身に付けるようにしましょう。

コメント