NumPy配列のスライス(ndarray の slice)とは、スクエアブラケット [] を使って、配列の任意の値を抽出する操作のことを言います。
NumPy配列のスライスには、Pythonのリストやタプルなどのシーケンスのスライスよりも、遥かに豊富なテクニックがあり、様々な操作が可能になっています。一つひとつ、しっかりと理解すればデータエンジニアリングの効率が非常に高まるのですが、初心者にとっては複雑で混乱しやすいものになっているのも事実です。
そこで、このページでは、配列のスライスのテクニックを1つずつ丁寧に解説していきます。
初心者の方は、まず「1. 1つの要素をスライス」「2. 開始位置・終了位置・間隔を指定してスライス」「6. 配列に対する値の代入」の3つの章を使いこなせるようになることを目指すと良いでしょう。そして実務上、さらに高度なスライスの知識やテクニックが必要な場面が訪れたら、インデックス配列によるスライスや、構造化ツールについてじっくり読み込んで見てください。
いずれにせよ、まずは一通り、このページの内容をすべて確認しておくことは重要です。配列のスライスで悩んだり詰まったりした時は、ぜひ見返すようにして頂ければと思います。
それでは解説を始めましょう。
1. 1つの要素をスライス
まずは、スライスの中で最も簡単な操作である、配列からの1つの要素の取り出しから見ていきましょう。
1次元配列から1つの要素をスライスする方法は、Pythonのシーケンス(リストやタプルなど)のスライスと同じです。それぞれ以下で解説しています。
しかし、2次元配列から1つの要素をスライスする場合は、リストやタプルとは違いがあります。
それぞれ実際のコードを見ながら確認していきましょう。
1.1. 1次元配列の場合
まずは1次元配列のスライスを見ていきます。繰り返しになりますが、この場合はPythonのリストやタプルなどのシーケンスのスライスと何も違いはありません。
以下の1次元配列 xを例に見ていきましょう。
import numpy as np
# 以下の配列を作成します
x = np.arange(1, 11)
x
この1次元配列 xの各要素は、それぞれ次のようにインデックス番号が振られた上でインデックス(=データベースに格納)されています。

重要:インデックス番号の数え方
インデックス番号は前から数える時は 0 から始まりますが、後ろから数える時は -1 から始まります。
この配列からの要素のスライスは、スクエアブラケット[] の中に抽出したい要素のインデックス番号を書くことで行います。
以下のコードでは、インデックス番号2の要素をスライスしています。
x[2]
負のインデックス番号を使ってスライスすることも可能です。
x[-2]
以上が1次元配列の要素のスライスです。
1.2. 2次元配列の場合
続いて、2次元配列からのスライスを見てみましょう。この場合はリストやタプルなどのPython標準シーケンスのスライスとは異なる点があります。
以下の2次元配列を例に解説します。
import numpy as np
x = np.arange(1, 11).reshape(2, 5)
x
この配列は、2次元軸である「行」と1次元軸である「列」に、それぞれ次のようにインデックス番号が割り当てられてインデックスされています(負のインデックス番号は省略しています)。
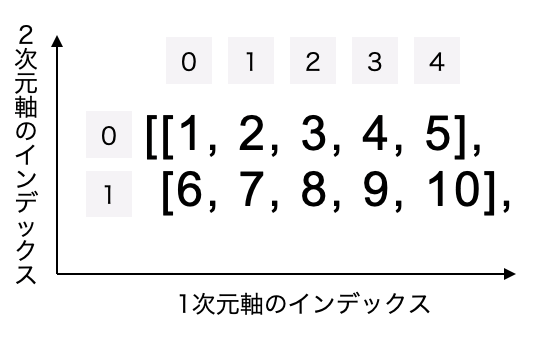
ここから1つの要素をスライスして抽出したい場合は、スクエアブラケットの中で、まず2次元軸のインデックスを指定した後にカンマで区切って、次に1次元軸のインデックスを指定します。
以下のコードをご確認ください。
# 2次元配列から2次元軸(行)のインデックス番号0、
# 1次元軸(列)のインデックス番号3をスライス
x[0, 3]
このコードでは、スクエアブラケット内の左側の数字で0で2次元軸(行)のインデックスを指定し、カンマで区切って書いた次の数字3で1次元軸(列)のインデックスを指定しています。結果、上の画像で見た通り、2次元軸のインデックス0と、1次元軸のインデックス3の位置にある4という数値を取得しています。
なお、ここの書き方にリストやタプルのスライスとは異なる点があります。
多次元のリストや多次元タプルのスライスの場合、list[0][3]というように、次元軸ごとにスクエアブラケットを書き、それらを繋げて書く必要があります。しかし、NumPyの配列では x[0, 3]と言うように、1つのスクエアブラケットの中にカンマで区切ることで、それぞれの次元軸を表現することができます。
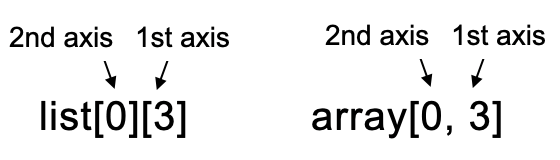
これはNumPy配列のスライスの大きな特徴の1つと言えるでしょう。NumPyでもリストやタプルのようにスクエアブラケットの重ねがけでスライスすることは可能ですが、とても非効率なので使用を控えましょう。この理由については、この後すぐに解説します。
スライス対象の配列よりも少ない次元数のインデックスを指定した場合
なお、スライス対象の配列よりも少ない数のインデックスを指定した場合、1つ下の次元の配列を抽出します。つまり、2次元配列で2次元軸のインデックスのみを指定した場合、スライスの結果は1次元配列になります。
この時に生成される配列のshapeは、元の配列の1次元軸の要素数と同じになります。例えば、shape(2, 5)の配列の2次元軸のインデックスを1つだけ指定した場合、生成される配列はshape(5, )になります。
以下のコードでご確認ください。
# 2次元軸のインデックスのみを指定した場合
x[0]
次のように書くと、1次元軸のインデックスのみを指定することができます。
x[:, 2]
このように、コロン : だけを指定した2次元軸は飛ばして、1次元軸のインデックスだけを指定して、要素を抽出することが可能です。これもリストやタプルにはなく、NumPyの配列でのみ可能な操作です。
こうした書き方については、次の項「2. 開始位置・終了位置・間隔を指定してスライス」の最後でもう一度触れます。
重要:NumPy配列でのスクエアブラケットの重ねがけはNG
上で、NumPy配列のスライスでは、リストやタプルのスライスのようにスクエアブラケットの重ねがけはしないようにと述べました。その理由を解説します。スライスで抽出した配列は、元々の配列のコピーではなくビューです。つまり、メモリに格納されている元々の配列の値を参照しています。「コピー」や「ビュー」については、詳しくは『NumPyの使い方まとめ – 初心者のためのクイックスタート』でご確認ください。
この理由から、NumPy配列でも、リストやタプルと同じように、x[0][3]と書いて要素を抽出することは可能ですが、決して推奨することはできません。この書き方は、x[0, 3]と結果は同じですが、遥かに非効率です。なぜなら、x[0] の一時的な配列を作成してから、x[2]の要素をスライスしていることになるからです。x[0, 3]は、そのような手間をかけずにワンステップで要素を抽出します。
重要:IDLやFortranに慣れている方へ
IDL や Fortran形式のメモリーオーダーに慣れている方のために解説しておくと、NumPyのインデックシングは、C-order 形式です。つまり、最後のインデックスのメモリ位置が最初に変わります。FortranやIDLは、最初のインデックスのメモリ位置が最も速く変わります。この違いは、大きな混乱の原因となる可能性があるので、ここで覚えておきましょう。Pythonからプログラミングの世界に入った方は、この点は理解できなくても問題ありません。
2. 開始位置・終了位置・間隔を指定してスライス
次に、配列から複数の要素を抽出するスライス方法を解説します。
NumPyの配列のスライスでも、リストやタプルのスライスと同じように、スクエアブラケットの中に[開始位置:終了位置:間隔]と書くことで、それぞれの次元ごとに複数の要素を抽出することができます。
これも、各次元軸ごとに指定することができます。実際に見ていきましょう。
2.1. 1次元配列の場合
まずは、以下の1次元配列を例に見ていきましょう。
import numpy as np
x = np.arange(1, 11)
x
開始位置と終了位置を指定
次のように書くと、開始位置と終了位置だけを指定したことになります。なお、抽出する要素に開始位置のインデックスの要素は含まれますが、終了位置のインデックスの要素は含まれません。
# インデックス番号2以上5未満の要素を抽出
x[2:5]
重要:開始位置の要素は含むが終了位置の要素は含まない
上のコードで見られるように、[開始位置:終了位置:間隔]を使ったスライスでは、開始位置のインデックスの要素は抽出されますが、終了位置のインデックスの要素は抽出されません。
開始位置だけを指定
次のように書くと開始位置だけを指定したことになります。この場合、指定の開始位置から最後の要素までをスライスします。
# インデックス番号5以上から最後の要素を指定
x[5:]
終了位置だけを指定
次のように書くと終了位置だけを指定したことになります。この場合、開始位置は常にインデックス番号0になります。繰り返しになりますが、終了位置の要素は抽出する配列には含まれません。
# インデックス番号-7より前の要素を抽出
x[:-7]
開始位置・終了位置・間隔を指定
インデックス1以上9未満の要素を2つ間隔でスライスしてみましょう。
# インデックス番号1以上9未満の要素を2つ間隔で抽出
x[1:9:2]
3の倍数のみを抽出したいとしたら、次のように指定すればOKです。
# 3の倍数のみを抽出
x[2::3]
逆順でスライス(間隔に負の値を指定)
[開始位置・終了位置・間隔] にはそれぞれ負の値を指定することもできます。開始位置と終了位置は、それぞれ負のインデックスを指定したことなり、間隔は逆順スライスを指定したことになります。
なお間隔に負の値を指定する時は、開始位置>終了位置 である必要があります。
実際に確認していきましょう。
すべての要素を逆順で抽出するには、次のように書きます。これは[9:0:-1]と同じです。開始位置と終了位置を省略すると、すべての要素を選択したことになります。
# 逆順スライス
x[::-1]
それではインデックス-3以下2超の範囲を2つ間隔で逆順スライスするにはどのように書けばいいでしょうか。
以下の通りです。
# -3 以下 2 超 の範囲を2つ間隔で逆順スライス
x[-3:2:-2]
ポイント:取得する要素の数の計算方法[開始位置:終了位置:間隔]で取得する要素の数は、(終了位置 - 開始位置)/間隔 で計算することができます。余りがでた時は商に1を足します。地味な知識ですが、大きなデータを扱う際はとても役に立ちますので、覚えておいて損はありません。
2.2. 2次元配列の場合
続いて2次元配列の場合を見ていきましょう。
スライス対象の配列が2次元以上の場合、[開始位置:終了位置:間隔]は、それぞれの次元軸ごとに指定することが可能です。
以下の2次元配列で確認してみましょう。
import numpy as np
x = np.arange(35).reshape(5, 7)
x
2次元配列では、このように2次元軸(行)のインデックスと1次元軸のインデックス(列)があります。
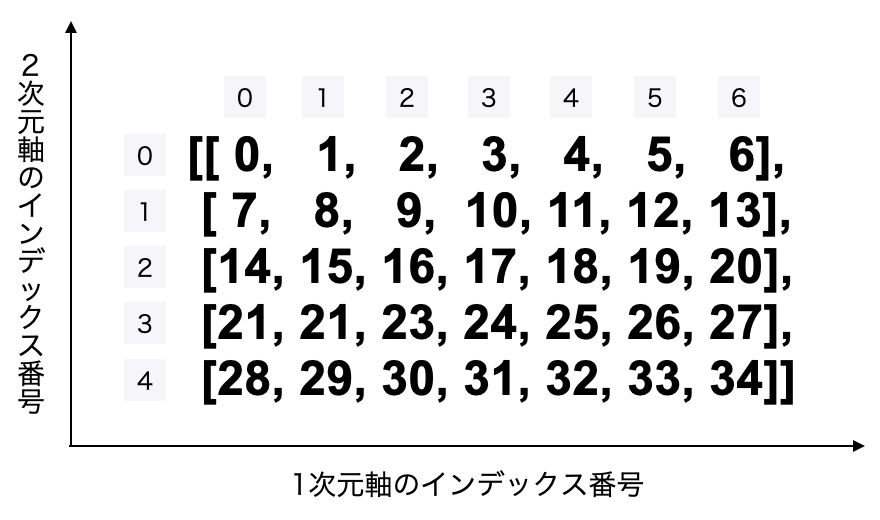
ちなみに3次元配列、4次元配列と増えていっても考え方は同じです。3次元軸として奥行きの要素が増え、4次元軸として、また一つ上の次元がの要素が増えるだけです。それぞれの軸にインデックス番号があります。
それでは、この2次元軸を対象に、[開始位置:終了位置:間隔]でスライスしていきます。
2次元軸のみ[開始位置:終了位置:間隔]を指定
まず2次元軸のみを指定してスライスしてみましょう。
以下のコードでは、2次元目である行のインデックス番号3以上の要素(つまり4行目と5行目)をスライスしています。
# 2次元軸(行)のインデックス番号3以上をスライス
x[3:]
次のコードでは、2次元軸のインデックス番号1以上4未満の要素(つまり2行目3行目)の要素をスライスしています。
# 2次元軸(行)のインデックス番号1以上4未満をスライス
x[1:4]
続いて、以下のコードでは2次元軸のインデックス番号1以上5未満の要素を2行置きの間隔でスライスしています。つまり、2行目4行目です。
# 2次元軸(行)のインデックス番号1以上を2つ間隔でスライス
x[1::2] # x[1:5:2]と同じ
2次元軸と1次元軸の[開始位置:終了位置:間隔]を指定
スクエアブラケット [] の中で、2次元軸の[開始位置:終了位置:間隔]を指定した後、カンマで区切って、次に1次元軸の[開始位置:終了位置:間隔]を指定することができます。
以下のコードでは、2次元軸のインデックス番号1以上4未満をスライスしてから、1次元軸のインデックス番号3をスライスしています。
# 2次元軸(行)のインデックス番号1以上4未満をスライス
# 続いて、1次元軸(列)のインデックス番号3をスライス
x[1:4, 3]
以下のコードは2次元軸のインデックスの指定は上のコードと同じで、1次元軸のインデックス番号3以上6未満にしたものです。
# 2次元軸(行)のインデックス番号1以上4未満をスライス
# 続いて、1次元軸(列)のインデックス番号3以上6未満をスライス
x[1:4, 3:6]
続いて、以下は2次元軸を2つ間隔でスライスしてから、1次元軸をインデックス1から2つ間隔でスライスしたものです。
# 2次元軸を0から2つ間隔でスライス
# 続いて、1次元軸を1から2つ間隔でスライス
x[::2, 1::2]
1次元軸のみ[開始位置:終了位置:間隔]を指定
さて、それでは2次元配列で1次元軸だけを指定してスライスしたい場合はどうすれば良いでしょうか。
その場合は、[:, 開始位置:終了位置] というように、2次元軸にはコロン( : )だけを置いて、カンマで繋ぎ、1次元軸の開始位置・終了位置・間隔を指定するだけです。
以下のコードをご確認ください。
# 1次元軸(列)のインデックス番号3以上6未満をスライス
x[:, 3:6]
もう一つ見ておきましょう。
# 1次元軸(列)のインデックス番号3以下を逆順でスライス
x[:, :3:-1]
注:コロン : とエリプシス ...
上のコードでは、コロン( : )のみを指定した次元軸は省略して、直接1次元軸のスライスを指定しています。コロン( : )のみの次元は、その次元軸の要素はすべて選択するという意味になります。例えば、2次元配列のスライスで2次元軸である行は置いておいて、1次元軸である列の要素のみ抽出したいというような場合に使います。
これは3次元配列以上になっても同じです。3次元配列で、3次元目と2次元目の軸を飛ばして、1次元軸のインデックスのみを指定したい場合は、[:, :, 開始位置:終了位置:間隔]と書きます。2次元軸のインデックスのみを指定したい場合は[:, 開始位置:終了位置:間隔] と書きます。[:, 開始位置:終了位置:間隔, :] と書いても構いません。
これと同じような働きをするものに、エリプシス (...) があります。エリプシスは「途中の軸をすべて省略する」という意味です。以下のコードでご確認ください。
>>> # 4次元配列の生成
>>> import numpy as np
>>> x = np.arange(1, 61).reshape(2, 2, 3, 5)
>>> # 3次元目と2次元目を省略してスライス
>>> x[0, ..., -1]
array([[ 5, 10, 15],
[20, 25, 30]])
>>> # 4,3,2次元目を省略してスライス
>>> x[..., 0]
array([[[ 1, 6, 11],
[16, 21, 26]],
[[31, 36, 41],
[46, 51, 56]]])
エリプシスは、基本的に4次元配列以上の次元数の多い巨大なデータを扱う際に使います。2次元配列以下では使いませんし、3次元でも使うことは少ないでしょう。これについては、「5. スライスの際に使える構造化ツール」で改めて触れたいと思います。
重要:スライスは元の配列のコピーではなくビューを返す。
上で述べたことの繰り返しになりますが、スライスは、元々の配列のコピーではなくビューを生成します。これは、リストやタプルのスライスとは異なる点です。もし、元々の配列がそれ以降必要ない場合は、以下のように明示的にcopyメソッドを使用します。そうすれば、del x と書くことで、元の配列に使われていたメモリスペースを解放することができます。
y = x[1:5:2, ::3].copy()
del x
「コピー」や「ビュー」については、詳しくは『NumPyの使い方まとめ – 初心者のためのクイックスタート』でご確認ください。
なお、ある配列を、別の配列でスライスすることも可能なのですが、この場合は、元の配列の要素を抽出した新しい配列(深いコピー)を生成することができます。次から、これらの点について解説します。
3. インデックス配列でスライス
NumPyの配列は、別の配列(またはリストなどの、配列に変換することのできる他のシーケンスオブジェクト。ただしタプルは不可。理由は最後に解説)でスライスすることができます。
「配列を配列でスライス」というとややこしいので、ここでは、スライスの対象となる配列を「オリジナル配列」、スライスの指定に使う配列を「インデックス配列」と呼ぶことにします。
なお、ここまで解説してきた[開始位置:終了位置:間隔]によるスライスを「基本的なスライス」としたら、インデックス配列によるスライスは「高度なスライス」と言えます。
基本的なスライスと高度なスライスの重要な違いとして、基本的なスライスでは元の配列のビュー(浅いコピー)を返しますが、高度なスライスではコピー(深いコピー)を返すという点にあります。そのため、高度なスライスの後、元の配列を消去すればメモリを解放することができます。プログラムのパフォーマンス向上のために、この点は覚えておきましょう。
それでは、この「高度なスライス」について解説していきます。高度なスライスに使うインデックス配列は、要素が整数の場合と、要素がブール値の場合があります。
まずは要素が整数のインデックス配列を使ったスライスについて解説します。
3.1. 要素が整数の配列でスライス
まずは、要素が整数のインデックス配列を使ったスライスを解説していきます。これには、オリジナル配列が1次元配列の場合と多次元配列の場合があります。
まずは1次元配列の場合を見ていきましょう。
オリジナル配列が1次元配列の場合
この場合はとてもシンプルでわかりやすいです。具体的には、インデックス配列の各数値要素は、オリジナル配列のどのインデックス番号の数値を抽出するかを指定します。
コードを見れば簡単に理解できるので、早速、以下のオリジナル配列を使って確認していきましょう。
import numpy as np
# オリジナル配列の作成
x = np.arange(10, 1, -1)
x
このオリジナル配列 xを、インデックス配列を使って、スライスしてみましょう。
以下のコードをご確認ください。
# スライス配列を使ってオリジナル配列をスライス
x[np.array([3, 3, 1, 8])]
インデックス配列は 3, 3, 1, 8 という整数の要素を持っています。これでオリジナル配列 xをスライスすると、対応するインデックス番号の要素が抽出されていることがわかります。さらに、生成される配列のshapeも、インデックス配列と同じになっています。
もちろん、インデックス配列の要素は負の整数でも構いません。
# 負の整数を要素として持つスライス配列でも可能
x[np.array([-6, -6, -8, -1])]
もし、インデックス配列の要素に、オリジナル配列の要素数よりも大きいインデックス番号の整数がある場合はエラーになります。
x[np.array([3, 3, 20, 8])]
一般的に、インデックス配列によるスライスによって生成される配列のshapeは、インデックス配列のshapeと同じになります。この特徴を使うと、生成する配列のshapeを自由にコントロールすることができます。
例えば、以下のコードでは、インデックス配列の 2x2 の二次元配列を使っています。
x[np.array([[1,1],[2,3]])]
ポイント:
要素が整数のインデックス配列でスライスした場合、生成される配列のshapeは、インデックス配列と同じものになる。
オリジナル配列が多次元配列の場合
オリジナル配列が多次元配列で、インデックス配列も多次元配列の場合、スライスはより複雑になっていきます。
これらは普通の用法ではありませんが、禁止されているわけでもありません。そして、時には良い解決策となり得ます。そのため、こういうやり方もあると知っておくと役立つ場合もあるでしょう。
ここでは、最もシンプルなケースとして、まずはオリジナル配列のみが2次元配列の場合を見ていきます。
以下の2次元配列をオリジナル配列とします。
import numpy as np
x = np.arange(35).reshape(5,7)
x
これに、インデックス配列として、次のように1次元配列を2つ渡してみます。
x[np.array([0, 2, 4]), np.array([0, 1, 2])]
このコードでは、2次元軸は array(0, 2, 4) を指定し、1次元軸は array(0, 1, 2) を指定しています。
この場合、2つのインデックス配列のshapeが一致しており、オリジナル配列が、スライスに使ったインデックス配列の数以上の次元数を持っていれば、生成される配列は1つのインデックス配列と同じshapeになります。上のコードの場合、インデックス配列は共にshape(3, )なので、生成された配列もshape(3, )です。
そして、抽出される値は、それぞれのインデックス配列で指定した軸が合致するところの値になります。つまり、上の例ではx[0, 0], x[2, 1], x[4,2] です。結果、array([0, 15, 30)] が抽出されています。
もし、インデックス配列同士のshapeが異なっていれば、まずブロードキャストが実行されます。そして、ブロードキャストでも、shapeを合致させることができなければ、エラーメッセージが返されます。以下では、インデックス配列の一方がshape(3, )で、もう一方がshape(2, )なので、ブロードキャスト不可能です。そのため、エラーになっています。
なお、ブロードキャストについては『NumPyの配列のブロードキャストのルール』をご確認ください。
x[np.array([0,2,4]), np.array([0,1])]
配列とスカラーの組み合わせであれば、必ずブロードキャスト可能です。例えば以下の場合は、x[0, 1], x[2, 1], x[4, 1] の要素を抽出していることと同じになります。
x[np.array([0,2,4]), 1]
もう少し複雑なケースを見てみましょう。インデックス配列で、オリジナル配列を部分的にスライスすることが可能です。
これを行うためには、その前にどういう出力結果になるのかをイメージするのに頭を悩ませることになりますが、例えば、次のように多次元のオリジナル配列に対して、インデックス配列を1つだけ渡すということができます。
x[np.array([0,2,4])]
この例では、2次元軸(行)のインデックス番号 0, 2, 4 の行の要素を抽出しています。結果、2次元軸に指定したインデックス配列の要素数 3 と、オリジナル配列の元々の1次元軸の要素数 7 が組み合わさり、shape(3, 7) の配列を生成しています。
このようなスライステクニックは、画像の値をRGBのトリプレットにマッピングするようなルックアップテーブルの作成に有効です。
ルックアップテーブルはshape(nlookup, 3)の配列になります。このような画像の配列を、shape(ny, nx)、dtype=np.unit8(サイズによるが別の整数タイプでも可能)のインデックス配列でスライスすれば、生成される配列はshape(ny, nx, 3)になり、この配列内のデータは、それぞれのピクセル位置ごとのRGBのトリプレットの値を示すものになります。
基本的に、このスライスによって生成される配列のshapeは、インデックス配列を結合したもの(またはインデックス配列がブロードキャストされたもの)と、オリジナル配列のうち使われていない軸が合わさったものになります。
以下にサンプルコードを載せておきます。最初から完全に理解できる必要はありません。こういう方法があるんだということを確認するぐらいで良いでしょう。
>>> palette = np.array(
... [[0, 0, 0], # 黒
... [255, 0, 0], # 赤
... [0, 255, 0], # 緑
... [0, 0, 255], # 青
... [255, 255, 255]]) # 白
>>> palette.shape
(5, 3)
# それぞれの値はパレットの色と対応
# 0=黒、 1=赤、 2=緑, 3=青、 4=白
>>> image = np.array(
... [[0, 1, 2, 0],
... [0, 3, 4, 0]])
>>> image.shape
(2, 4)
# (2, 4, 3) のカラーイメージを取得
>>> palette[image]
array(
[[[ 0, 0, 0],
[255, 0, 0],
[ 0, 255, 0],
[ 0, 0, 0]],
[[ 0, 0, 0],
[ 0, 0, 255],
[255, 255, 255],
[ 0, 0, 0]]])
# shapeはインデックス配列(2, 4)とオリジナル配列(5, 3)のうち
# 指定されていない軸(この場合は1次元軸)がくっついたものになる。
>>> palette[image].shape
(2, 4, 3)
3.2. 要素がブール値の配列でスライス
インデックス配列として、要素が整数の配列以外に、要素がブール値の配列を使うこともできます。
この場合は、要素が整数のインデックス配列を使った時とは大きく異なります。以下の一連のコードでは、最もシンプルな使い方を表現しています。
import numpy as np
# オリジナル配列の作成
x = np.arange(35).reshape(5,7)
x
# 要素がブール値の配列(マスクされた配列)を作成
b = x > 20
b
# 要素がブール値の配列(マスクされた配列)でスライス
x[b]
要素が整数の配列をインデックス配列に用いた場合とは異なり、要素がブール値の配列の場合、生成される配列は、ブール配列のTrueに該当する全ての要素を格納した1次元配列になります。上のコードの場合では、値が20超の場合にTrueであり、Trueに該当する要素のみ抽出されています。
なお、IDLやFortranに慣れている方に、混乱を防ぐためにお伝えしておくと、この時、オリジナル配列の要素は、常に C-style のメモリオーダで順番に取得され戻されます。
また、生成される配列の要素の数は、x[np.nonzero(b)]と同じになります。そして、生成される配列はデータのコピーであり、ビューではありません。
ポイント:
要素がブール値のインデックス配列(マスクされた配列)でスライスする場合、基本的に、オリジナル配列とインデックス配列のshapeが合致している必要があります。両者のshapeが合致している場合、スライスで生成される配列のshapeは、インデックス配列のTrueの要素の数と同じになる。
もし、オリジナル配列 xの次元数が、要素がブール値のインデックス配列の次元数よりも大きい場合、生成される配列も多次元になります。以下のコードをご覧ください。
x[b[:,5]]
'''
b[:,5] == array([False, False, False, True, True])
'''
このコードでは、オリジナル配列から4行目と5行目が選択され、かつ、2次元配列として生成されています。
基本的に、ブール値配列の次元数がオリジナル配列の次元数より小さい場合は、 x[b, ...] と同じことです。つまり、 オリジナル配列 x は インデックス配列 b と、そのほか必要な数の : によってスライスされるということです。
そのため、生成される配列のshapeは、次元数がオリジナル配列からスライスで指定した次元軸の数だけ減った上で、その中の最も大きな次元軸の要素数がブール値配列のTrueの要素の数と同じで、他の次元はオリジナル配列の残る次元の要素数と同じものになります。
例えば、Trueの要素が4つのshape(2, 3)の2次元ブール配列で、shape(2, 3, 5)のオリジナル3次元配列をスライスすると、生成される配列はshape(4, 5)の2次元配列になります。
以下のコードをご覧ください。
import numpy as np
x = np.arange(30).reshape(2,3,5)
b = np.array([[True, True, False], [False, True, True]])
x[b]
このコードでは、オリジナル配列はshape(2, 3, 5)です。そして、ブール値のインデックス配列でスライスする際、スライス軸は1つだけです。そのため、生成される配列はオリジナル配列が1次元減少した2次元配列になります。この2次元配列の最も大きな次元の要素数は、インデックス配列のTrueの数と同じ4 になります。あと残っているのは、オリジナル配列の1次元目の5だけなので、生成される配列はshape(4, 5)になるというわけです。
ポイント:
要素がブール値のインデックス配列b の次元数が、オリジナル配列 xの次元数よりも低い場合、生成される配列の次元数は x.ndim - b.ndim - その他スライスを指定した次元軸の数 になります。shapeは、最も大きな次元軸ではインデックス配列に格納されているTrueの数、それ以降は残ったオリジナル配列の各次元軸の要素数が継承されます。
4. 基本的なスライスと高度なスライスの組み合わせ
「基本的なスライス([開始位置:終了位置:間隔]の指定によるスライス)」と「高度なスライス(インデックス配列によるスライス)」は組み合わせることができます。
早速、以下のコードをご覧ください。
import numpy as np
x = np.arange(35).reshape(5,7)
x[np.array([0, 2, 4]), 1:3]
事実上、スライスとインデックス配列の実行は独立しています。上のコードでは、インデックス配列の実行で、2次元軸のインデックス番号0, 2, 4(1列目3列目5列目)を抽出し、基本スライスの実行で1次元軸のインデックス番号1と2(2行目と3行目)を抽出しています。
これは、以下のコードと同じです。
x[:, 1:3][np.array([0, 2, 4]), :]
同じように、基本的なスライスと、要素がブール値のインデックス配列によるスライスを組み合わせることもできます。以下の一連のコードをご覧ください。
b = x>20
b
x[b[:,5],1:3]
これは以下のコードと同じことです。
x[:, 1:3][b[:, 5]]
5. スライスの際に使える構造化ツール
構造化ツールとは、配列同士のshapeの簡単なマッチングを促進するために用意されているものです。これができるようになると、配列の表現や代入の際に、わざわざreshapeメソッドなどを使って、shapeを調整する手間を省略することができます。
ここでは、newaxisオブジェクトを解説し、上でも触れたエリプシス(…)にも改めて触れたいと思います。
5.1. newaxisオブジェクトで次元軸を追加
スライスオブジェクト [] の中に、np.newaxisオブジェクトを加えると、それを加えた場所に要素数が1の新しい次元を付与することができます。
以下のコードをご覧ください。
import numpy as np
x = np.arange(35).reshape(5,7)
x
x.shape
x[:,np.newaxis,:].shape
shape(5, 7)の配列を、x[:,np.newaxis,:]とスライスすることで、指定の場所に次元数が1つ増えていることがわかります。これによって、本来は操作を行うためにreshapeが必要な2つの配列を手軽に組み合わせることができます。
例として以下のコードをご覧ください。
>>> import numpy as np
>>> y = np.arange(5)
array([0, 1, 2, 3, 4])
>>> y[:,np.newaxis]
array([[0],
[1],
[2],
[3],
[4]])
>>> y[np.newaxis,:]
array([[0, 1, 2, 3, 4]])
>>> y[:,np.newaxis] + y[np.newaxis,:]
array([[0, 1, 2, 3, 4],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 6],
[3, 4, 5, 6, 7],
[4, 5, 6, 7, 8]])
5.2. エリプシス(...)で次元軸を省略
上の方でも触れましたが、エリプシス(...)は、残りの未特定の次元のすべてを省略(=全てを選択)していることを示すために使うことができます。
例えば、3次元配列で、3次元目と2次元目の軸を飛ばして、1次元軸のインデックスのみを指定したい場合は、[:, :, 開始位置:終了位置:間隔]と書きます。2次元軸のインデックスのみを指定したい場合は[:, 開始位置:終了位置:間隔] と書きます。
先ほど使ったサンプルコードをもう一度載せておきます。
>>> # 4次元配列の生成
>>> import numpy as np
>>> x = np.arange(1, 61).reshape(2, 2, 3, 5)
>>> # 3次元目と2次元目を省略してスライス
>>> x[0, ..., -1]
array([[ 5, 10, 15],
[20, 25, 30]])
>>> # 4,3,2次元目を省略してスライス
>>> x[..., 0]
array([[[ 1, 6, 11],
[16, 21, 26]],
[[31, 36, 41],
[46, 51, 56]]])
さらに以下の4次元配列で更に確認してみましょう。
import numpy as np
z = np.arange(81).reshape(3,3,3,3)
z
これを、以下のコードのようにEllipsis(...)を使ってスライスしてみましょう。
z[1,...,2]
これは、4次元目軸ではインデックス1を抽出してから、3次元軸と2次元軸は省略(= すべてのインデックスを抽出)し、最後に1次元軸ではインデックス2を抽出していることと同じになります。
これは以下のコードと同じことです。
z[1,:,:,2]
6. 配列に対する値の代入
ここまで解説した「基本的なスライス」や「高度なスライス」を使って、配列に値を代入することもできます。
代入される値は、shapeが対応している(同じshapeかブロードキャスト可能)必要があります。次の配列を使って、いくつか例を見ていきましょう。
import numpy as np
x = np.arange(10)
x
以下のコードでは、インデックス番号2以上7未満の要素に10を代入しています。スカラーはブロードキャスト可能なので、指定の要素の値がすべて10に変更されています。
x[2:7] = 10
x
以下では、同じ箇所に。np.arange(5) の各要素を代入しています。変更する要素の数と、代入する要素の数は揃っている必要があります。
x[2:7] = np.arange(5)
x
数値の代入では、データ型に注意する必要があります。例えば、要素がint型(整数)の配列にfloat型(浮動小数点数)を代入すると、int型(整数)に変換されます。
x[1] = 1.2
x[1]
要素がint型やfloat型の配列に、complex型(複素数)を代入しようとすると、そもそもcomplex型のint型やfloat型への変換が不可能なため、エラーになります。
x[1] = 1.2j
いくつかの参照(配列とマスクされたインダイス)と違って、代入は常に元々の配列のデータに対して行われます。
しかし、いくつかの操作は、意図した通りに実行されない場合もあります。例えば、以下のコードをご覧ください。
x = np.arange(0, 50, 10)
x
x[np.array([1, 1, 3, 1])] += 1
x
このコードでは、インデックス1の要素に数値を複数回足し合わせたいのですが、実際には1回しか足し算が行われていません。
これは、新しい配列は、常に一時的な配列としてオリジナル配列から引っ張ってこられるために起こります。つまり、このコードでは、インデックス番号1の要素を引っ張る度に、その値が10にリセットされているのです。
7. プログラムの中で様々な数値のインダイスに対応する
インデックスの構文はとても強力ですが、様々な数のインダイスに対応するには限界があります。例えば、想定される様々な次元数を持つ引数に対応する特別なコードを書く必要なしに、様々な次元数の引数を管理する関数を作成するというような場合です。このような場合はどうすれば良いでしょうか。
これについては、次の点を覚えておくと役立ちます。
- スライスオブジェクト
[]の中ににタプルを与えると、そのタプルはインダイスのリストとして解釈される。
例えば、以下のコードをご覧ください。
import numpy as np
x = np.arange(81).reshape(3,3,3,3)
indices = (1, 1, 1, 1)
x[indices]
つまり、任意の数値のインダイスをタプルで構築することができるということです。そして、関数作成などの際は、そのタプルをスライスの指定に使うことができます。
Pythonでは、スライスは、プログラムの中で、slice関数を使うことで特定することができます。以下のコードをご覧ください。
indices = (1,1,1,slice(0,2)) # [1,1,1,0:2]と同じ
x[indices]
同じように、エリプシス も、Ellipsisオブジェクトを使うことでコードで特定することができます。
indices = (1, Ellipsis, 1) # [1,...,1]と同じ
x[indices]
この理由から、np.nonzero関数の出力を直接インデックスとして使うことも可能です。この関数は、常にインデックス配列のタプルを返すからです。
「3.インデックス配列でスライス」の冒頭で、「NumPyの配列は、別の配列(またはリストなどの、配列に変換することのできる他のシーケンスオブジェクト。ただしタプルは不可)でスライスすることができます。」と書きましたが、タプルがリストのように自動的に配列に変換されないようになっているのは、このためです。
例えば、次のような書き方だと、大きな配列を生成します。これは、リストはインデックス配列に変換されてしまうからです。
以下の違いをしっかりと抑えておきましょう。
>>> import numpy as np
>>> x = np.arange(81).reshape(3,3,3,3)
>>> x[[1,1,1,1]] .shape
(4, 3, 3, 3)
>>> x[(1,1,1,1)].shape
()
違いは、以下の点にあります。
リストは、「3.インデックス配列でスライス」で解説したインデックス配列に自動的に変換されて処理されます。そのため、前者のコードは、x[np.array([1, 1, 1, 1)] と同じです。
タプルは、インデックス配列に自動的に変換されることはありません。そのため、後者のコードは、x[1, 1, 1, 1]と同じです。
8. まとめ
以上がNumPyの配列のスライスの基本と応用のすべてです。
配列のスライスで悩んだり詰まったりした時は、ぜひ見返すようにして頂ければと思います。

コメント