NumPyのlog関数で対数を取得する4つの方法まとめ

2021 5/06

2020年10月2日 2021年5月6日

NumPyには、対数を計算する関数として、log関数が用意されています。対数は、統計学や機械学習において、とてもよく使います。

それでは「対数」とは何でしょうか。簡単に復習しましょう。

対数は log_ab = x における x のことです。log_ab は「底a を何乗すれば bになるか？」を表します。そして、その答えである x のことを「底をa とするb の対数」と言います。

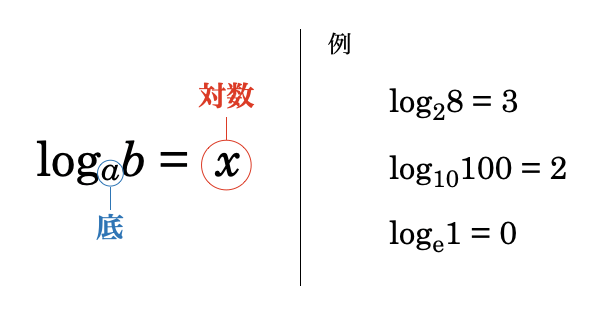
例えば log₂8 は「2 を何乗すれば 8 になるか」なので、答えは 3 です。log₁₀100 は「10を何乗すれば100になるか」なので、答えは 2 です。底がネイピア数e のものは「自然対数」と言います。自然対数は、単純に指数関数の真逆のものです。

そして、NumPyには複数の底に対応できるように、以下の4つの種類のlog関数が用意されています。

log: 底をネイピア数e とするb の対数
log10: 底を10 とするb の対数
log2: 底を2 とするb の対数
log1p: 底をネイピア数e とするb+1 の対数

このページでは、それぞれの関数について解説します。

1. 書式

早速、書き方を確認しましょう。

np.log関数

書き方:

np.log(x),  np.log2(x),  np.log10(x),  np.log1p(x)

引数	型	解説
x	array_like	任意の配列を渡します。
* この他に、キーワード引数としてufunc(ユニバーサル・ファンクション)を使用可能です。具体的には、out, where, axes, axis, keepdims, casting, order, dtype, subok, signature, extobj です。しかし、これらは高度な操作を行いたい時に使うものであり、基本的には使いません。

戻り値:

ndarray：
渡した配列x のそれぞれの要素ごとに計算した対数を要素とする新しい配列を返します。x がスカラーの場合は、戻り値もスカラー（1つの数値のみの配列）になります。

2. サンプルコード

それでは、以下の配列の各要素の対数を取得しましょう。

In [1]:

import numpy as np
x = np.linspace(1, 2, 12)
x

Out[1]:

array([1.        , 1.09090909, 1.18181818, 1.27272727, 1.36363636,
       1.45454545, 1.54545455, 1.63636364, 1.72727273, 1.81818182,
       1.90909091, 2.        ])

この配列は、以下で示すように一次関数になっています。

In [2]:

import matplotlib.pyplot as plt
plt.plot(x, label="x")
plt.legend()
plt.show()

それでは、それぞれの関数を使って対数を取得しましょう。

In [3]:

# 自然対数（底をeとする対数）
np.log(x)

Out[3]:

array([0.        , 0.08701138, 0.16705408, 0.24116206, 0.31015493,
       0.37469345, 0.43531807, 0.49247649, 0.54654371, 0.597837  ,
       0.64662716, 0.69314718])

In [4]:

#  底を2とする対数
np.log2(x)

Out[4]:

array([0.        , 0.12553088, 0.2410081 , 0.3479233 , 0.44745898,
       0.54056838, 0.62803122, 0.71049338, 0.78849589, 0.86249648,
       0.9328858 , 1.        ])

In [5]:

#  底を10とする対数
np.log10(x)

Out[5]:

array([0.        , 0.03778856, 0.07255067, 0.10473535, 0.13469857,
       0.1627273 , 0.18905624, 0.21387982, 0.23736092, 0.25963731,
       0.28082661, 0.30103   ])

In [6]:

#  底をeとするx+1の対数
np.log1p(x)

Out[6]:

array([0.69314718, 0.73759894, 0.78015856, 0.82098055, 0.86020127,
       0.89794159, 0.93430924, 0.96940056, 1.00330211, 1.03609193,
       1.06784063, 1.09861229])

なお、np.log1p(x) は np.log(1+x) と同じです。ただし、配列x の要素が実数である場合、np.log1pの方が計算精度に優れています。

それでは、それぞれの対数をグラフに描いて比較してみましょう。

In [7]:

import matplotlib.pyplot as plt
x = np.linspace(1,10,100)
plt.plot(x, label="x")
plt.plot(np.log(x), label="log")
plt.plot(np.log2(x), label="log2")
plt.plot(np.log10(x), label="log10")
plt.plot(np.log1p(x), label="log1p")
plt.legend()
plt.show()