numpy.random.normal関数で正規分布から乱数配列を作成する方法

numpy.random.normal関数は、任意の平均・標準偏差の正規分布（「ガウス分布」とも言う）から乱数を生成する関数です。このページでは、この関数について解説します。

1. 書式

np.random.normal(loc=0.0, scale=1.0, size=None)

numpy.random.normalは、任意の正規分布（ガウス分布）の中から、乱数を生成します。正規分布とは何かについて簡潔に解説しておきます。

正規分布とは

ガウス分布の確率密度は、次の式で表されます。

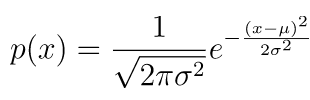
μ は平均値、σ は標準偏差、σ² は分散です。この関数のピークは平均値にあり、広がりは x+σ と x-σ まであります。正規分布では平均値にある数値の方が得られやすく、そこから離れた値ほど得られにくくなるということです。

これを図にしたものが以下です。

まずは平均値0、標準偏差10の正規分布です。

In [1]:

import numpy as np
import matplotlib.pyplot as plt
rand3 = np.random.normal(0, 10, 1000000)
plt.hist(rand3, bins=1000)
plt.xlabel('x')
plt.ylabel('frequency')
plt.xlim(-60, 60)
plt.show()

これが平均20・標準偏差10だと次のようになります。

In [2]:

import numpy as np
import matplotlib.pyplot as plt
rand3 = np.random.normal(20, 10, 1000000)
plt.hist(rand3, bins=1000)
plt.xlabel('x')
plt.ylabel('frequency')
plt.xlim(-40, 40)
plt.show()

numpy.random.normalは、こうした正規分布（ガウス分布）の中から、乱数を生成します。

2. サンプルコード

それでは、この関数を使って乱数を生成してみましょう。

平均値と標準偏差だけを指定すると、その正規分布の中から値を1つ返します。

# 平均を0に、標準偏差を0.1の正規分布から数値を取得
import numpy as np
np.random.normal(0, 0.1)

0.0002619446306721982

第三引数でshapeを指定すると、正規分布からランダムに取り出した値を要素とした配列を生成します。

# 1次元配列で値を取得
np.random.normal(0, 0.1, 3)

array([0.13415695, 0.05907306, 0.03957742])

2次元配列以上を出力する時は、shapeをタプルで渡します。shape属性については『NumPyのshape属性 – 配列の形状の確認と変更』で解説しています。

# 2次元配列で値を取得
np.random.normal(0, 0.1, (2, 3))

array([[-0.04348408, -0.03998982,  0.13836223],
       [-0.07294112,  0.07036188, -0.00540975]])

それでは、平均がμ、分散がσ² の正規分布 N(μ, σ²) から乱数を生成するには、どう書けば良いでしょうか。

例えば、N(3, 6.25)としましょう。この場合、分散(σ²)が6.25なので、標準偏差のsigma(σ)は、√6.25=2.5です。そのため、次のように書きます。

# N(3, 6.25)
np.random.normal(3, 2.5, (3, 2))

array([[3.70240629, 2.99122748],
       [1.31339454, 0.39931026],
       [1.39874727, 5.55294345]])

3. まとめ

以上、numpy.random.normalは、任意の平均と標準偏差の正規分布から乱数を生成する関数です。現在は、この関数は使わずに、Generatot.normalメソッドを使います。こちらの方が遥かに高速です。今後、新しい乱数を生成する際は、Generator.normalメソッドを使うようにしましょう。

なお、正規分布から乱数を生成する関数には、以下のものもあります。

• random.randn
• random.sntandard.normal

これらはどちらも、平均0・標準偏差0.1の標準正規分布から乱数を生成する関数です。現在では、これらの関数も使わずに、Generator.standard_normalメソッドを使います。

• Generator.standard_normal

併せて確認しておくと良いでしょう。