機械学習は、近年で驚くほど多くの場所で使われるようになりました。GoogleやFacebook、Amazonはもちろん、国内国外で機械学習をコア技術としている注目スタートアップの数がめざましく増えています。
機械学習とは、簡単に言うと、今までは人が行なっていたグループ分けやデータに基づく予測などの作業を、人間よりも高い精度で機械で実現することができる技術のことです。
そうした作業を機械に任せることで、人間はより本質的で生産的なことに時間を使えるようになりますので、非常に注目されています。
ここでは、Pythonでの機械学習の入門編として、まず機械学習とは何かを解説した後に、具体的な手順と、実際の例として3つの機械学習モデルを、実際にコードを書きながら解説していきます。
ぜひ、最初の一歩としてお役立て頂ければと思います。
1. 機械学習とは何か
機械学習は大きくわけて3つあります。
- 教師あり学習
- 教師なし学習
- 強化学習
教師なし学習や強化学習はビジネスでの事例が、少なく、現状、成功しているシステムのほとんどは教師あり学習です。またこの記事は、機械学習の入門編ということもあり、ここでは教師あり学習について解説したいと思います。
教師なし学習や、強化学習、ディープラーニングなども、おいおい解説記事を用意したいと思います。とはいえ、いきなり教師あり学習の詳細に入る前に、それぞれの違いを簡単に理解しておきましょう。
1.1. 教師あり学習
教師あり学習は、質問と同時に答えも教えるものです。たくさんのデータと答えを与えることで、それに習熟した上で、また新たに質問を与えていきます。そうすると、どんどん習熟度が上がり、精度が高まっていきます。
例えば、手書き文字を読めるモデルを作るなら、無数の手書き文字のデータと、それが何という文字かの答えのファイルを与えます。システムは、手書き文字と答えの関連性を学習し習熟することで、新たに手書き文字を見たときに、それが何の文字なのかを判別できるようになります。
音声認識ができるモデルを作るなら、人間の音声データと、その音声に対応するテキストファイル（答え）をセットにして与えます。システムは、こうしたセットを使って、音声とテキストの関連性を学習し習熟することで、新たに音声を聞いたときに、それを文章にできるようになります。
1.2. 教師なし学習
教師なし学習は、データだけがあって、その答えとなるファイルはありません。多くのデータから何らかの特徴を見出しグループ分け（クラスタリング）を行ったり、複雑なデータを単純化（次元削減）するといったことを目的としています。
1.3. 強化学習
強化学習は、動物にエサを与えて芸を仕込むように、何か良い行動をした時には報酬を得られるというアルゴリズムを作ります。これによって、学習を重ねるごとに、AI自身で自然と良い行動を導き出せるようになります。これは、ロボットや、ゲームなどで使われています。
2. 教師あり学習の基礎知識
それでは、ここから教師あり学習について解説していきます。まずは基本的な知識を押さえておきましょう。
2.1. 教師あり学習の手順
教師あり学習は次のような手順で行います。
- データセットを読み込む
- データセットを訓練データとテストデータに分ける
- 訓練データと教師データを学習器にかけて訓練する
- テストデータを使って性能を評価する
流れを簡潔に解説します。
教師あり学習では、まずデータを訓練データとテストデータに分けておきます。もちろん教師あり学習なので、データの答えとなる教師データ（ターゲット、ラベルと言う）も用意します。
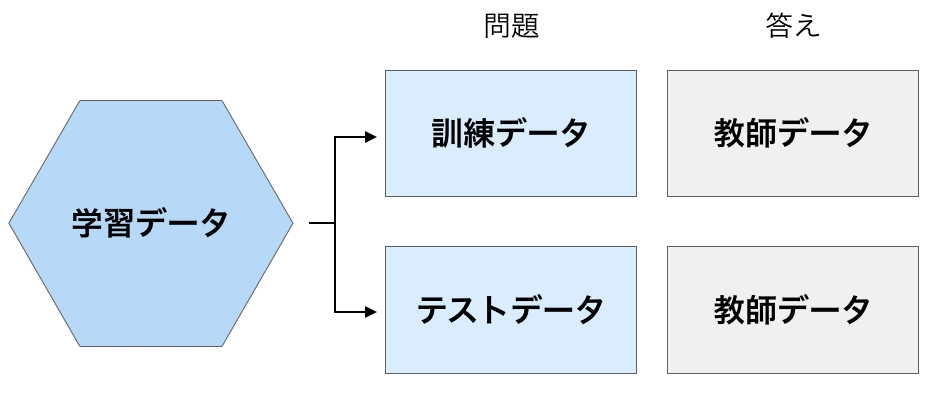
そして訓練データをプログラム（学習器という）に入れて、習熟させることで学習済みモデル（分類器）を作ります。
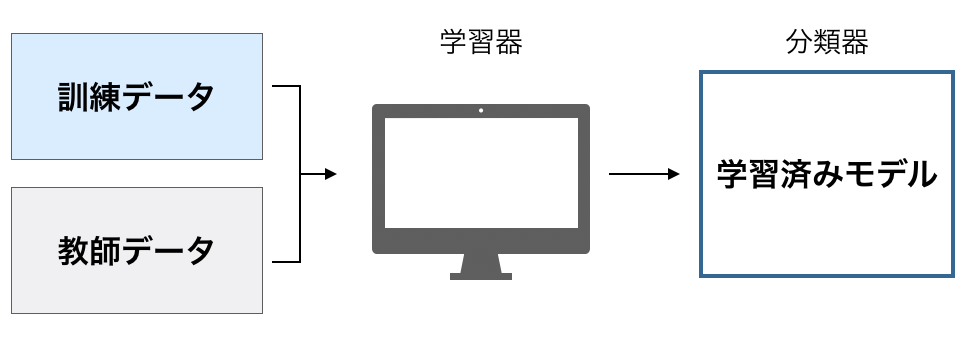
次に、学習済みモデル（分類器）にテストデータを入れて、正しい答えが出てくるかどうかの性能を試験します。
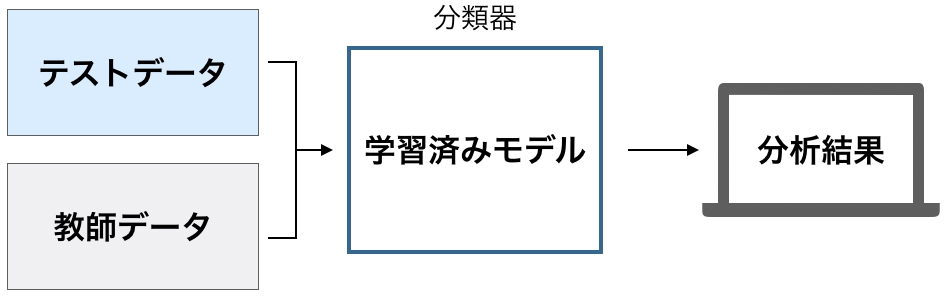
ここで性能が不十分であれば、十分なものになるまで学習の方法を改善してから繰り返し学習させることで、最終的に性能が高い学習モデルを作ります。
2.2. 学習器アルゴリズムと学習データ
2.2.1. 学習器アルゴリズム
機械学習プログラムを作るには、学習器のアルゴリズムが重要です。最初に性能が高い学習アルゴリズムを使うか性能が低い学習アルゴリズムを使うかで、プロジェクトにかかる時間が大きく異なるからです。
そうは言っても、学習器のプログラムを書くには、多大な経験と知識、計画を要します。しかし、嬉しいことに、現在では、高度な学習器アルゴリズムが多数用意されているライブラリが無償有償問わず、いくつか存在します。
最も使われているのはGoogleが公開しているTensorFlow（テンサーフロー）か、scikit-learn（サイキットラーン）でしょう。
ここではscikit-learn（サイキット・ラーン）を使いたいと思います。
scikit-learnは、オープンソースで公開されており、個人利用/商用利用を問わず、誰でも無償で利用することができるライブラリです。初心者が機械学習を学ぶには、最適のライブラリと言えるでしょう。
このライブラリを使うのに必要なライブラリは、すべてAnacondaに含まれているので、Anacondaをインストールしていれば、すぐに機械学習プログラミングを始めることができます。
2.2.2. 学習データ
機械学習を行うには、学習器アルゴリズムだけではなく、大量の学習データも必要です。これも、機械学習を学ぶ人のために、大量の学習データを公開してくれているサイトがあります。
まずは、scikit-learnの学習データセットです。ここには機械学習プログラミングの学習のための教材となる多数のトイデータがあります。
他には、UCI Machine Learning Repository があります。ここには様々な学習データが揃っており、今も新しいデータが追加されています。
手書き数字の学習データが大量に存在するサイトもあります。それがTHE MINIST DATABASEです。
これらを使って、簡単な機械学習を行ってみましょう。
3. 手書き数字の機械学習
それでは、ここから実際に機械学習を実践してみましょう。
ここでは、はじめの一歩として、0~9の手書き数字の画像データを学習してから、画像を見てどの数字なのかを判読するモデル（分類器）を作ってみましょう。
3.1. データセットの読み込み
ここからはscikit-learnのライブラリとデータセットを利用します。そこで、まずはscikit-learnのデータの読み込み方法から解説します。
scikit-learnには、機械学習の学習用に複数のトイデータセットがあります。Toy datasetsを確認してみてください。ここでは、この中にある手書き数字のデータセットload_digits()を使います。
scikit-learnにあるデータを読み込むには、まずsklearnパッケージのdatasetsモジュールをインポートします。次に、手書き数字のデータセットをload_digits()で、変数digitsに読み込んでいます。
from sklearn import datasets #scikit-learnのデータセットモジュールのインポート
digits=datasets.load_digits() #手書き数字のデータセットの読み込み
これでデータセットを読み込みました。最初なので、データセットについても詳しく解説しておきます。まず、データセットの内容をdir()関数で確認してみましょう。
dir(digits)
このように、digitsには5種類のデータが入っています。内容はそれぞれ次の通りです。
| 名前 | データの内容 |
| DESCR | データセットの説明文 |
| data | 画像データ（訓練データとテストデータ） |
| images | 画像データ(8行×8列にしたもの） |
| target | 画像データの答えとなる数字（教師データと検証用データ） |
| target_names | targetの画像データの数字の名前（数字の種類） |
中身を見てみたい場合は、pirnt関数で出力することができます。試しにデータセットの説明文’DESCR’を見てみましょう。
print(digits.DESCR)
簡潔に解説しておきます。
このデータセットには、’data”に画像データが、’target’にそれぞれの画像データの正解の数字が教師データ（ターゲット）として入っています。画像データはdigits.data、それに対応する教師データはdigits.targetで取り出すことができます。
それでは、このデータの構造をshapeメソッドで調べてみましょう。
digits.data.shape
digits.target.shape
これを見ると、画像データ’data’は1797行×64列の2次元配列データであることが分かります。一方で、教師データ’target’は1797行のみの1次元配列データです。
ここから、画像データは手書き数字の画像ファイルではないことがわかります。’DESCR’にも書いてあるのですが、画像データは8×8ピクセルの合計64ピクセルの枠の中で、それぞれ1ピクセルずつ16のグレイスケールによって、色の濃さを0~16で示したものです。これによって数字を表しています。つまり、8×8の64ピクセルなので1行64列が、ちょうど1文字分のデータになります。これが1797行あるので、画像データには1797の手書き数字が入っています。
そして教師データには、この1797個の手書き数字の答えが入っています。例えば、1文字目の画像データの答えは「0」、2文字目は「1」、1797文字目は「8」というように正解の数字が入っているのです。
参考に、1行目のデータを見てみましょう。digits.imagesには、digits.dataの64ピクセルのグレイスケールが、8×8のマトリックスで格納されています。以下をご覧ください。一番最初の文字データを抽出したものです。
digits.images[0]
数字が大きいほど色が濃く、小さいほど色が薄いものです。それでは、このデータを使って、実際の画像を復元してみましょう。
画像を描画するには、matplotlibというライブラリにあるpyplotモジュールの、matshow()メソッドを使います。それで復元したものが以下です。
import matplotlib.pyplot as plt
plt.matshow(digits.images[0], cmap="Greys")
plt.show()
見てみると、数字の「0」に見えますね。実際に確認してみましょう。
digits.target[0]
やはり0です。
ここで読み込んだデータセットには、このような0~9までの数字の画像データとその答えである教師データが1797個含まれています。
3.2. 訓練データとテストデータを分ける
ここまででデータセットの読み込みを行いました。次のステップは、このデータセットを訓練データとテストデータに分けることです。
ここでは、データセットの’data’と’target’の前半分を訓練データとそれに対応する教師データ、後半分をテストデータとそれに対応する教師データにします。次のコードをご覧ください。
n=len(digits.data)*1//2 #データを半分にわける
X_training = digits.data[:n] #dataの前半分
Y_training = digits.target[:n] #targetの前半分
X_test = digits.data[n:] #dataの後半分
Y_test = digits.target[n:] #targetの後半分
まず、データの総数はlen(digits.data)です。この半分を訓練データにしたいので、len(digits.data)*1//2を行なっています。”//”演算子を使っているのは、整数にしたいからです。詳しくは、「Pythonの演算子」をご覧ください。
その後、訓練データとテストデータに相当する変数に、データセットのデータをスライスして代入しています。スライシングについては、「Pythonのリストのスライス」で解説しています。
それぞれの変数に入れたデータをshapeメソッドで確認しておきましょう。
print([i.shape for i in [X_training, Y_training, X_test, Y_test]])
この通り、訓練データは898個、テストデータは899個に別れています。
3.3. 訓練データを学習器にかけて学習させる
これで訓練データができました。ここでいよいよ機械学習を行います。上述のように、学習アルゴリズムを作るには、様々な分野で高度なスキルや経験、発想が必要です。
そのため通常は、オープンソースの学習アルゴリズムを使います。ここでは、scikit-learnのライブラリにあるsvmモジュールのSVCというアルゴリズムを使います。
scikit-learnには、学習アルゴリズムがいくつか用意されています。以下が一覧です。
- Classification
- Regression
- Clustering
- Dimensionality reduction
- Model selection
- Preprocessing
svmモジュールは、この中のClassification（データの特徴を分析して、カテゴリー毎に分類する学習アルゴリズム）です。以下のドキュメントも読んでおくと良いでしょう。
SVCアルゴリズムのドキュメント：sklearn.svm.SVC
以下をご覧ください。
from sklearn import svm #svmモジュールをインポート
lng = svm.SVC(gamma=0.001) #学習器を作る
lng.fit(X_training, Y_training) #学習器に訓練データと教師データを渡す
svmモジュールのSVCをlngに代入しています。SVC関数の引数のgammaは、関数計算のカーネル係数です。ここでは詳しく理解する必要はありません。気になる場合は、scikit-learnのSVCのページを見てみましょう。
このモジュールのfit()メソッドは、引数に訓練データと教師データを与えて、学習器に学習させるものです。
3.4. テストデータを使って性能を評価する
テストデータを評価する方法は色々ありますので、それぞれ見ていきましょう。ここでは、様々な方法で評価を行って、機械学習の性能をさらに高める方法を模索する姿勢が重要です。
3.4.1. score()メソッド
まずは、score()メソッドを使ってみましょう。メソッドの引数に、テスト用の訓練データとテスト用の教師データを渡すと正答率を返してくれます。
print(lng.score(X_test, Y_test))
ここでは96.9%の正答率だったことがわかります。
3.4.2. predict()メソッド
学習器にpredict()メソッドを実行すると、次のようにテストデータの識別結果を numpy の配列で返してくれます。
predicted = lng.predict(X_test) #判別結果をNumpy配列で取り出す
predicted
教師データもnumpyの配列なので、次のように、比較演算子を使って、誤答の数の合計を調べることができます。詳しくは「Nupmy配列の数値演算」をご覧ください。
(Y_test != predicted).sum() #教師データと一致しなかった数（誤答数）を合計
このように人工知能が間違った回答をした数が28個であったことがわかります。
3.4.3. metrics.classification_report()
sklearnモジュールのmetrics()メソッドのmetrics.classification_report()を使うと、それぞれの数字の正答率がわかります。以下をご覧ください。
メソッドのドキュメント：sklearn.metrics.classification_report
from sklearn import metrics
print(metrics.classification_report(Y_test, predicted))
このように、引数に教師データとpredited()メソッドで作った判別結果を渡すと、解析データを返してくれます。まず、最上段の項目について解説します。
- precision：正答率
- recall：再現率
- f1-score：F値
- support：個数
例えば、人工知能がある手書き画像を「4」であると判別したとします。その時、実際に「4」だった正答率が98%です。そして、「4」の手書き画像を「4」と正しく分類できた割合が再現率である95%です。F値は判別結果の統計的な有効性です。こうしたデータを正確に読み解くには、統計学の知識やスキルが求められます。
3.4.4. metrics.confusion_matrix()
metrics.confusion_matrix()を使うと、各文字ごとの正答数と誤答数がわかります。引数には教師データとpredicted()メソッドで作った判別結果を渡します。
メソッドのドキュメント：sklearn.metrics.confusion_matrix
from sklearn import metrics
print(metrics.confusion_matrix(Y_test, predicted))
1行目が「0」で最後の10行目が「9」です。そして1列目が「0」で最後の10列目が「9」です。
1行目は「0」の判別結果です。87個正解して1個を「4」と誤答したことがわかります。2行目は「1」で、88個正解して3個誤答しています。それぞれ「2」「8」「9」と一回ずつ誤答しています。最も誤答が多かったのは4行目の「3」で79個正解で12個誤答しています。「8」と間違えた個数が5個、「7」と間違えた個数が4個、「5」と間違えた個数が3個です。
それでは間違いが多かった箇所の手書き数字の画像と、判別結果を表示してみましょう。
import matplotlib.pyplot as plt
imgs_yt_preds = list(zip(digits.images[n:], Y_test, predicted))
for index, (image, y_t, pred) in enumerate(imgs_yt_preds[704:716]):
plt.subplot(3, 4, index+1)
plt.axis('off')
plt.tight_layout()
plt.imshow(image, cmap="Greys", interpolation="nearest")
plt.title(f'right:{y_t} result:{pred}', fontsize=12)
plt.show()
rightが正しい答え、resultが判別結果です。見てみると、「3」を「7」と誤答しているのが多いですね。人間の目で見てみても、なかなか判別がつき難いので、これはしかたがないように思います。
3.5. 機械学習の手順の再まとめ
ここまで見てきたように、教師あり学習は、
- データセットを読み込む
- データセットを訓練データとテストデータに分ける
- 訓練データと教師データを学習器にかけて訓練する
- テストデータを使って性能を評価する
という手順で行うということを覚えておきましょう。当然、コードもこの手順と同じ流れで書いていきます。また性能評価については、様々な方法で行い、多角的に分析することが重要です。scikit-learnには、様々な分析ツールが揃っているので、上手に活用しましょう。
4. アヤメの品種判別の機械学習
続いて、他の機械学習の例も見ていきましょう。
4.1. データセットの読み込み
scikit-learnのトイデータセットには、花のアヤメのデータセットがあります。このデータセットはload_iris()で読み込みます。
from sklearn import datasets
iris = datasets.load_iris() #irisデータセットの読み込み
dir()関数で、このデータセットに含まれている情報を確認してみましょう。
dir(iris)
手書き数字のdigits()のデータと同じように5種類のデータが入っていることを確認できます。
次に、iris.DESCRでデータセットの説明文を見ましょう。
print(iris.DESCR)
ここから、Setosa、Versicolour、Virginicaの3種類のIrisのデータが、それぞれ50個ずつ合計150個入っていることがわかります。また、花のsepal（がく片）の長さと幅、petal（花弁）の長さと幅のデータがcm単位で入っていることも書かれています。
それでは、それぞれのデータの構造を調べてみましょう。このデータセットには、3種類のアヤメの計測データ’data’（訓練/テストデータ）と、それぞれがどの花なのかを示す教師データ’target’が入っています。
これらのデータは、それぞれiris.data、iris.targetで取り出すことができます。このデータの構造をshape()メソッドで調べてみましょう。
X = iris.data #訓練/テストデータ
Y = iris.target #教師データ
print(X.shape)
print(Y.shape)
このように、iris.dataは150行×4列の二次元配列データ、iris.targetは150行の一次元配列データであることがわかります。
次に、データの中身を見てみましょう。
X
このように、計測データ’data’には一行に4つの数字が入っています。
次にfeature_namesを確認しましょう。
iris.feature_names
このように、sepal length（がく片の長さ）、sepal width（がく片の幅）、 petal length（花弁の長さ）、 petal width（花弁の幅）の4つの属性があることがわかります。つまり、’data’の4列の数字の属性は、左から、この順に並んでいるということです。
次に教師用データ’target’の中身を見てみましょう。
Y
このように0、1、2の数字が入っています。0はsetosa、1はversicolour、2はvirginicaです。
入っているデータを散布図で視覚化すると次のようになります（がく片の長さがx軸とがく片の幅がy軸）。
import matplotlib.pyplot as plt
plt.scatter(X[:50, 0], X[:50, 1], color='r', marker='^', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='g', marker='+', label='versicolour')
plt.scatter(X[100:, 0], X[100:, 1], color='b', marker='x', label='virginica')
plt.title("Iris Plants Database")
plt.xlabel('sepal length(cm)')
plt.ylabel('sepal width(cm)')
plt.legend()
plt.show()
花弁の幅をx軸、花弁の長さをy軸にとった散布図では次のようになります。
import matplotlib.pyplot as plt
plt.scatter(X[:50, 2], X[:50, 3], color='r', marker='^', label='setosa')
plt.scatter(X[50:100, 2], X[50:100, 3], color='g', marker='+', label='versicolour')
plt.scatter(X[100:, 2], X[100:, 3], color='b', marker='x', label='virginica')
plt.title("Iris Plants Database")
plt.xlabel('petal length(cm)')
plt.ylabel('petal width(cm)')
plt.legend()
plt.show()
これを見ると、がく片の長さと幅、花弁の長さと幅だけでアヤメの品種を高い精度で見分けられることがわかりますね。
4.2. 機械学習を行う
さて、Irisのデータセットの中身がわかったところで、ここから機械学習を行いましょう。今回もアヤメの分類なので、Classificationアルゴリズムのsvmモジュールを使います。
コードは手書き文字の時と同じなので、詳細は割愛します。
from sklearn import datasets
from sklearn import svm
iris = datasets.load_iris() #データセッtの読み込み
X=iris.data #訓練/テストデータ
Y=iris.target #教師データ
n = len(X)//2 #データを半分に分割
X_training, X_test = X[:n], X[n:] #dataの前半分を訓練データ、後半分をテストデータに
Y_training, Y_test = Y[:n], Y[n:] #教師データを前半分と後半分に分ける
lng = svm.SVC() #学習モデル
lng.fit(X_training, Y_training) #データを学習器にかける
4.3. 性能を評価する
それでは、テストデータを使って性能を評価してみましょう。
4.3.1. score()メソッド
score()メソッドで正答率を評価してみましょう。
print(lng.score(X_test, Y_test))
結果、正答率はたったの33.3%にしか達していないことがわかります。これでは明らかに問題がありますね。
4.3.2. 性能が低い原因を考える
このような時は人工知能の性能を高めるにはどうすれば良いのかを考えることが重要です。まずは、ここまで低い正答率になってしまった原因を考えましょう。
データセットを訓練用データとテストデータに分ける時に、単純に前半分、後半分で分けてしまったからです。データセットの構造を思い出して見ましょう。
データの最初の50個はsetosaのデータです。51~100個はversicolourのデータです。101~150個はvirginicaのデータです。このように、それぞれの品種のアヤメのデータは50個ずつ並んでいます。つまり、訓練データにはsetosaのデータ50個とversicolourのデータ25個、テストデータにはversicolourのデータ25個、virginicaのデータ50個が入っているということです。
この訓練データを使って学習してもvirginicaを見分けられるようにはなりません。
今回は、このように答えが分かりきっていますが、実際でも、性能評価して原因や改善策を模索する姿勢が非常に重要です。さて、答えがわかったところで、次に改善していきましょう。
4.3.3. 訓練データとテストデータを作り直す
データセットを訓練データとテストデータに分ける方法に問題があったので、次はデータをシャッフルして訓練データとテストデータに分ける方法を試してみましょう。
次のコードをご覧ください。
from sklearn.model_selection import ShuffleSplit
ss = ShuffleSplit(train_size=0.5, test_size=0.5, random_state=0)
これで分割比率を50vs50に設定したShuffleSplitのインスタンス ss を作りました。インスタンスについては「Pythonのクラス(class)の使い方まとめ | オブジェクト指向入門」をご確認ください。ShuffleSplitはscikit-learnのsklearn.model_selectionモジュールのメソッドです。最初はわからなくても問題ないので、ドキュメントや実例に多く触れて慣れていきましょう。
それでは、これを使って、訓練データと教師データ、テストデータと教師データを作りましょう。
train_index, test_index = next(ss.split(X))
X_train, Y_train = X[train_index], Y[train_index] #訓練データ
X_test, Y_test = X[test_index], Y[test_index] #テストデータ
next()関数はPythonの組み込み関数でイテレータやジェネレータから要素を一つずつ取り出すものです。参考に『Pythonのイテレータとジェネレータの使い方まとめ』をご覧ください。これを使って、next(ss.split(X)を実行すると、次のように訓練データとテストデータのインデックス番号の配列が作られます。
next(ss.split(X))
最初の配列をtrain_indexに、二つ目の配列をtest_indexに代入しています。
さて、データを学習データとテストデータにランダムに分けることができたので、もう一度訓練とテストを行ってみましょう。
lng = svm.SVC()
lng.fit(X_train, Y_train)
print(lng.score(X_test, Y_test))
結果、正答率は93.3%となり、大きく上昇しました。
なお学習器のアルゴリズムは様々なものがあります。ここまではSVMという学習器を使っていますが、これ以外のも多数のものがあり、それぞれ異なる機能やオプションがあります。
ここでは例として、linear_modelモジュールのLogisitcRegressionという学習器を試してみましょう。
ドキュメント：sklearn.linear_model: Generalized Linear Models
from sklearn import linear_model
lng = linear_model.LogisticRegression()
lng.fit(X_train, Y_train)
print(lng.score(X_test, Y_test))
結果、正答率は84.0%なので、svm.SVC()の方が良い結果となっています。このように学習器も一つではないので、最適なものを探せるようになると良いでしょう。そのためには、プログラミングだけでなく数学や統計学についての知識も必要になってきます。最初から全てを理解することはできません。
コードを書きながら、一つずつ地道に努力を重ねていきましょう。
5. 住宅価格分析の機械学習
ここまでは、svm.SVC()を使った分類・識別モデルでした。最後は、ある変数が変化した時の変化を予測するモデルである線形回帰モデルを作ってみましょう。
5.1. データセットの読み込み
scikit-learnのトイデータセットからボストンの住宅価格のデータセットを読み込みます。
from sklearn import datasets
boston = datasets.load_boston()
データセットの構造を確認しましょう。
dir(boston)
‘DESCR’を開いて、データセットの詳細を確認しましょう。
print(boston.DESCR)
ここから506個のデータがあり、属性は13種類、MEDVが教師データの住宅価格であることがわかります。それぞれの属性を解説しておきます。
| 属性 | 説明 |
| CRIM | 人口1人当たりの犯罪発生数 |
| ZN | 25,000平方フィート以上の住居区画の占める割合 |
| INDUS | 小売業以外の商業が占める面積の割合 |
| CHAS | チャールズ川の周辺(1が川の周辺で0がそれ以外） |
| NOX | NOx濃度 |
| RM | 平均部屋数 |
| AGE | 1940年より前に建てられた物件の割合 |
| DIS | 5つのボストン市の雇用施設からの距離 |
| RAD | 環状高速道路へのアクセスのしやすさ |
| TAX | 10.000ドルあたりの不動産税率の総計 |
| PTRATIO | 町毎の児童と教師の比率 |
| B | 町毎の黒人の比率 |
| LSTAT | 給与の低い職業に就いている人口の割合(%) |
| MEDV | 住宅価格（単位：＄1000） |
データセットの項目が多いので、pandasモジュールのDataFrame型に変換して扱いやすくしてみましょう。pandasはPythonに対して数多くのデータ解析機能を提供しているライブラリです。機械学習を行うには、必ず触れることになるので、ここで取り扱っておきましょう。pandasの公式ドキュメントにも目を通しておくと良いでしょう。
DataFrameは2次元配列と似たデータ型で、これを使うと、次のようにデータを見やすくすることができます。
from pandas import DataFrame #pandasモジュール
boston_df = DataFrame(boston.data) #型をDataFrame型に変換
boston_df.columns = boston.feature_names #列名の設定
boston_df["price"] = boston.target #住宅価格の追加
print(boston_df[:5]) #最初の5行だけprintする
ここでは、pandasモジュールには色々な解析機能があるということを覚えておいてください。
5.2. 機械学習を行う
ここでは、部屋数(RM)と住宅価格(price)を使って回帰分析のモデルを作りましょう。上のコードのboston_df.columnsに列名を設定しているため、部屋数のデータはDataFrame(boston_df[“RM”])で取り出すことができます。住宅価格はtargetに入っているのでboston.targetで取り出すことができます。回帰モデルはscikit-learnのLinearRegression()で作成します。
次のコードをご覧ください。
rooms_train = DataFrame(boston_df["RM"]) #部屋数のデータを抜き出す
Y_train = boston.target #テスト用の教師データ（住宅価格）
from sklearn import linear_model #線形回帰モジュールのインポート
model = linear_model.LinearRegression() #回帰モデル
model.fit(rooms_train, Y_train) #データを入れて訓練
5.3. 性能を評価する
それでは、訓練したモデルで回帰直線を引いてみます。
テストデータ rooms_test は、rooms_trainの最小値から最大値まで0.1ずつ刻んだものを用意します。そしてprice_testに、訓練済みのモデルを使って求めた住宅価格を入れます。
#テストデータの作成
rooms_test=DataFrame(np.arange(rooms_train.min(), rooms_train.max(), 0.1))
prices_test=model.predict(rooms_test)
次のコードで、実際の部屋数rooms_trainと実際の価格y_trainを散布図で表示し、テストデータの部屋数rooms_testと予想価格prices_testで回帰直線を引きます。
見てみると、実際の価格と、回帰分析による予想価格の傾向がだいたい一致していることがわかります。
import matplotlib.pyplot as plt
import numpy as np
plt.scatter(np.array(rooms_train), Y_train, alpha=0.5) #訓練データの散布図
plt.plot(rooms_test, prices_test, c="r") #回帰直線
plt.title("Boston House Prices dataset")
plt.xlabel("rooms")
plt.ylabel("prices")
plt.show()
なお今回は、部屋の数から住宅価格を予測する単回帰モデルを作りましたが、部屋の数以外のパラメータを使っても問題ありません。
例えば、以下は犯罪発生率から住宅価格を予測するモデルです。
import seaborn as sns
boston=datasets.load_boston()
boston_df=DataFrame(boston.data)
boston_df.columns=boston.feature_names
boston_df["Price"] = boston.target
sns.lmplot(x="CRIM", y="Price", data=boston_df)
plt.show()
次に、給与の低い職業に就いている人口の割合から住宅価格を予測するモデルです。
import seaborn as sns
boston=datasets.load_boston()
boston_df=DataFrame(boston.data)
boston_df.columns=boston.feature_names
boston_df["Price"] = boston.target
sns.lmplot(x="LSTAT", y="Price", data=boston_df)
plt.show()
単回帰分析モデルだけではなく重回帰分析モデルを作ることもできますし、その他多数の高度な分析モデルを作ることができます。焦らず、一つずつ身につけていきましょう。
6. まとめ
ここで開設したのは、機械学習のほんの入り口に過ぎません。学習器は多数あり、様々なモデルを作ることができます。
また、学習器に入れるデータの量や質が向上すればするほど、さらに精度の高いモデルを作ることができ、その判断や予測は人間よりもはるかに正確なものになっていきます。
そのためには、データを学習させて終わりではなく、もっと高い性能になるには、どうすればいいのか、ボトルネックとなっている部分を解析し、それを解決していく発想力も必要になります。
そうしたプロセスを超えて素晴らしい機械学習モデルを作れたとしたら、それは社会にとっても素晴らしい貢献になるでしょう。
Python初心者におすすめのプログラミングスクール
「未経験からでもPythonを学べるプログラミングスクールを探しているけど、色々ありすぎてわからない」なら、次の３つのプログラミングスクールから選んでおけば間違いはありません。
Aidemy Premium：全くの初心者ができるだけ効率よく短期間で実務的に活躍できるAI人材になることを目的とした講座。キャリアカウンセリングや転職エージェントの紹介などの転職支援も充実しており、受講者の転職成功率が高い。
AIジョブカレ
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
データミックス：プログラミング経験者のビジネスマンが、更なるキャリアアップのためにデータの処理方法を学んでデータサイエンティストになるための講座。転職だけでなく起業やフリーランスとして独立する人も多い。Python初心者用の対策講座もある。
特に、あなたが以下のような目標を持っているなら、この中から選んでおけば間違いはないでしょう。
・未経験からPythonエンジニアとして就職・転職したい
・AIエンジニアやデータサイエンティストとしてキャリアアップしたい
・起業やフリーランスを視野に入れたい
理由は「Python初心者のためのおすすめプログラミングスクール3選」で解説しています。
コメント