NumPyのrandomモジュールの全ての乱数配列の作成方法まとめ

NumPyのrandomモジュールでは、様々な種類の乱数の配列を作成するためのメソッドが豊富に用意されています。これらを使うことでデータサイエンスの効率が大きく向上します。

ここでは、現時点(NumPy ver1.19)で使用可能な乱数配列メソッドを全て紹介します。全てを覚える必要はありませんが、こうした様々な乱数配列を作成できることを知っておくと、思いがけず必要となった時にすぐに対処できるようになります。そのため、一通り眺めておくのは有益でしょう。

それでは、早速見ていきましょう。

乱数配列の作成メソッドの一覧

最初に、必要となった時に見返せるように、使用可能な全メソッド・それぞれのメソッドの確率分布・それぞれの確率分布の簡単な説明の一覧を載せておきます。

以上です。それでは、それぞれの確率分布の乱数について理解を深めていきましょう。

はじめに

最初に前提知識として、NumPyで乱数配列を作成する方法の概要を簡単に解説します。

実は、NumPyのver1.17前後で乱数配列の作成方法は変更されています。それまでは関数を使って行っていましたが、現在では default_rng というコンストラクタを使ってジェネレータオブジェクトを作り、このジェネレータオブジェクトに対して各種メソッドを使うという方法で行うようになっています。

例として以下のコードを見比べてみましょう。どちらも正規分布の乱数配列を作成するものです。

''' ver1.17までの乱数配列の作成方法 '''
import numpy as np 
np.random.normal(size=5)  # 関数で作成

array([ 0.10877441, -0.87121138,  0.55981045,  0.15692073, -1.49172027])

''' ver1.17以降の乱数配列の作成方法 '''
rng = np.random.default_rng()  # ジェネレータを作成
rng.normal(size=5)  # ジェネレータに対して乱数メソッドを呼び出す

array([-0.76568253, -0.44885266,  0.31481089, -1.88706256, -0.32766818])

新しい方法の方がコードとしては1行増えますが、こちらの方が処理が高速であり、大量のデータを扱う科学技術計算に適しています。そのため、このページではver1.17以降の方法に則って使い方を解説していきます。

なお、default_rngコンストラクタについては、以下のページで詳しく解説しています。

• 『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』

それでは、様々な確率分布の乱数配列を作成する方法を確認していきましょう。

1. 最もよく使われる確率分布

ここでは、最もよく使われる確率分布として、一様分布と正規分布を解説し、それぞれのメソッドの使い方を見ていきます。

1.1. 一様分布の乱数配列

一様分布の乱数配列を作成するメソッドには以下の3つがあります。

上2つは、どちらも連続一様分布（要素が小数[float型]）の乱数配列を作成します。3つ目のものは、離散一様分布（要素が整数[int型]）の乱数配列を作成します。

連続一様分布

連続一様分布とは、以下のヒストグラムで表している通り、指定の範囲内のすべての数値が等しい確率で得られるような確率分布のことです。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.random(100000)
plt.hist(r)
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

この連続一様分布から乱数配列を作成するメソッドは2つあります。

• Generator.random: 0.0以上1.0以下の範囲の連続一様分布から乱数配列を作成
• Generator.uniform: 任意の範囲の連続一様分布から乱数配列を作成

それぞれ見ていきましょう。

random

randomメソッドは、0.0以上1.0以下の範囲の連続一様分布（「標準連続一様分布」といいます）から乱数配列を作成します。引数には、作成する配列の形状をタプル（1次元配列の場合は整数でも可）で渡します。

import numpy as np
rng = np.random.default_rng()
rng.random((5, 2))

array([[0.84289844, 0.53341161],
       [0.00583559, 0.74624116],
       [0.83016219, 0.75619421],
       [0.71384606, 0.83475581],
       [0.90974598, 0.16365828]])

オプション引数には dtype= と out= があり、配列のデータ型や出力先を変更することができます。詳しくは、以下で解説しています。

• 『Generators.random – 標準連続一様分布から乱数配列を生成する方法』

uniform

uniformメソッドでは、任意の範囲の連続一様分布の乱数配列を作成することができます。第一引数に最小値、第二引数に最大値、第三引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.uniform(-1., 1., (5, 2))

array([[-0.28227863,  0.87340776],
       [ 0.00759625,  0.41427524],
       [-0.5665792 , -0.61015378],
       [-0.71516571,  0.54619392],
       [ 0.51999728,  0.6974623 ]])

他にオプション引数はありません。以下のページでさらに詳しく解説しています。

• 『Generator.uniform – 連続一様分布から任意の範囲の乱数配列を作成する方法』

離散一様分布

離散一様分布とは、範囲内の整数がすべて等しい確率で現れる確率分布のことです。ヒストグラムにすると、以下のように、それぞれの乱数が飛び飛びに分布することから「離散」と名付けられています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.integers(1, 7, 100000)
plt.hist(r, bins=30)
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

離散一様分布から乱数配列を作成するには integers メソッドを使います。

integers

integers メソッドでは第一引数に最小値、第二引数に最大値、第三匹数に作成する配列の形状を渡します。作成される配列に、最小値は含まれますが、最大値は含まれません。

import numpy as np
rng = np.random.default_rng()
rng.integers(1, 7, 6)

array([2, 4, 3, 6, 3, 5])

他にオプション引数 endpoint= で、最大値を作成する乱数配列の中に含むかどうかを指定することができます。詳しくは、以下のページをご覧ください。

• 『Generator.integers – 離散一様分布から整数の乱数配列を作成する方法』

1.2. 正規分布の乱数配列

正規分布の乱数配列を作成するメソッドには以下の3つがあります。

いずれも要素が浮動小数点数(float型)の乱数配列を作成します。

正規分布

正規分布（またはガウス分布）とは、以下のヒストグラムのように、平均値に近い数値ほど高確率で見られ、そこから離れるほど見られる確率が低くなる分布のことです。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.standard_normal(100000)
plt.hist(r, bins=100)
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

この正規分布から乱数配列を作成するメソッドは2つあります。

• Generator.standard_normal: 平均0・標準偏差1.0の正規分布から乱数配列を作成
• Generator.normal: 任意の平均・標準偏差の正規分布から乱数配列を作成

standard_normal

standard_normalメソッドは、平均が0・標準偏差が1.0の標準正規分布から乱数配列を作成します。引数には、作成する配列の形状を整数（1次元配列の場合）または整数のタプル（多次元配列の場合）で渡します。

import numpy as np
rng = np.random.default_rng()
rng.standard_normal(5)

array([ 2.14073476,  0.59962273, -0.3171614 , -1.53329783,  0.90598331])

他にオプション引数 dtype= でデータ型を変更したり、out= で乱数配列の出力先を変更したりすることが可能です。例えば、dtype= で整数型を指定すれば、離散型の正規分布になります。詳しくは、以下のページで解説しています。

• 『Generator.standard_normal – 標準正規分布から乱数配列を生成する方法』

normal

normalメソッドでは、任意の平均値・標準偏差の正規分布から乱数配列を作成することができます。第一引数に平均値、第二引数に分散、第三引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.normal(40, 20, (5, ))

array([13.43708726, 61.69890887, 56.4742042 , 53.90141596, 37.15468028])

詳しくは以下のページで解説しています。

• 『Generator.normal – 任意の平均・標準偏差の正規分布から乱数配列を作成』

多変量正規分布

多変量正規分布（または「多次元正規分布」もしくは「結合正規分布」）は、一次元の正規分布を高次元に一般化したものです。多変量正規分布の場合、平均値は平均(average)ではなく中央値(center)を意味し、分散は標準偏差^**2(standard deviation^**2)ではなく幅^**2(width^**2)を意味します。

multivariate_normal

多変量一様分布を作成するには、multivariate_normalメソッドを使います。第一引数には中央値、第二引数には共分散行列、第三引数には生成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.multivariate_normal([1, 2], [[1, 0], [0, 1]], (3, 3))

array([[[-0.68498338, -0.21575292],
        [-0.83729389,  1.9882497 ],
        [ 1.43219092,  0.77628466]],

       [[ 0.98958928, -0.67695891],
        [ 0.86325469,  2.30409428],
        [ 1.7501053 ,  2.11872772]],

       [[-0.01580087,  2.28045099],
        [ 2.07632235,  0.85912367],
        [ 2.66826674,  2.15374486]]])

以下は多変量正規分布を2次元でプロットしたものです。

import numpy as np
mean = [0, 0]
cov = [[1, 0], [0, 100]]  # 対角共分散

import matplotlib.pyplot as plt
x, y = np.random.default_rng().multivariate_normal(mean, cov, 5000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()

詳しくは以下のページでご確認ください。

• 『Generator.multivariate_normal – 多変量正規分布から乱数配列を作成する方法』

2. 離散確率分布

ここでは離散一様分布について解説し、それぞれの確率分布に対応するメソッドの使い方を見ていきます。

基本的に、離散一様分布はコインやサイコロを投げた時の裏表の分布や、成功確率が一定の試行を、指定の回数繰り返した時の成功数や失敗数の分布など、確率論的などといった問題に使います。

それではそれぞれ見ていきましょう。

2.1. 二項分布の乱数配列

二項分布の乱数配列を作成するメソッドには2つあり、二項分布の多変量解析である多項分布を作成するメソッドが1つあります。

すべて離散確率分布であり、要素が整数(int型)の配列を作成します。

二項分布

二項分布とは、互いに独立したベルヌーイ試行（結果が成功か失敗のいずれかである試行）をn回行ったときの、成功回数を描いた離散確率分布です。例えば、以下のヒストグラムは、成功確率20%の事象を10回行うのを1セットとして、10000セット行った時の1セット当たりの成功回数の分布です。

import  numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.binomial(10, .20, 10000)
count, bins, ignored = plt.hist(s, 30, density=True)

これが二項分布です。

NumPyでは通常の二項分布の乱数配列を作成するbinomialメソッドが用意されています。

binomial

binomialメソッドは、第一引数に1セット当たりの成功回数、第二引数に成功確率、第三引数に作成する乱数配列の形状を渡します。

import  numpy as np
rng = np.random.default_rng()
rng.binomial(10, .15, (5, ))

array([2, 2, 1, 2, 2])

これ以外の引数はありません。以下のページでは、さらに詳しく解説しています。

• 『Generator.binomial – 二項分布から乱数配列を作成する方法』

負の二項分布

負の二項分布は、n回の成功を達成するまでに、何回失敗するかの確率を表す分布です。二項分布は、n回試行した時の成功回数の分布なので、これらはお互いに反対のものに焦点を当てています。

NumPyでは、この負の二項分布の乱数配列を作成するnegative_binomialメソッドが用意されています。

negative_binomial

negative_binomialメソッドは、第一引数に目標とする成功回数、第二引数に成功確率、第三引数に作成する乱数配列の形状を渡します。以下のコードは、成功確率15%の事象を、累計10回成功するまでに、何回失敗したかの乱数配列を作成しています。

import  numpy as np
rng = np.random.default_rng()
rng.negative_binomial(10, .15, (5, ))

array([62, 47, 82, 48, 64])

これも他にオプション引数はありません。以下のページで詳しく解説しています。

• 『Generator.negative_binomial – 負の二項分布から乱数を作成』

多項分布

多項分布は二項分布の多変量解析です。二項分布は、結果が成功か失敗の2つしかないベルヌーイ試行の分布ですが、多項分布は、例えばサイコロを100回振った時の1から6までの各出目の出現数といった多変量の乱数の配列を作成することができます。

NumPyでは、この多項分布から乱数配列を作成するmultinomialメソッドが備えられています。

multinomial

multinomialメソッドは、第一引数に試行回数、第二引数にそれぞれの出目の出現確率、第三引数に作成する乱数配列の形状を渡します。例えば、サイコロを100回振って、1から6の出目がそれぞれ何回出るかの乱数を得るには次のように書きます。

import  numpy as np
rng = np.random.default_rng()
rng.multinomial(100, [1/6.]*6, 1)

array([[21, 12, 13, 17, 17, 20]])

他にオプション引数はありません。以下のページでより詳しく解説しています。

• 『Generator.multinomial – 多項分布から乱数配列を作成』

2.2. 幾何分布の乱数配列

幾何分布の乱数配列の作成については、NumPyには以下の3つのメソッドが備えられています。

これらはすべて離散確率分布であり、要素が整数(int型)の配列を作成します。

幾何分布

幾何分布は、ベルヌーイ試行を繰り返して何回目で成功するかの確率分布です。例えば、成功確率40%の事象をはじめて成功するまでの試行回数は、以下のような分布になります。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.geometric(0.4, 100000)
plt.hist(r, bins=30, range=(1, 7))
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

NumPyでは、幾何分布の乱数を取得するのに、geometricメソッドが用意されています。

geometric

geometricメソッドは、第一引数に成功確率、第二引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.geometric(0.4, (5,))

array([3, 3, 7, 2, 2])

他に引数はありません。以下のページで解説しています。

• 『Generator.geometric – 幾何分布から乱数配列を作成する方法』

超幾何分布

超幾何分布は、例えば、黒石と白石が入っている壺から、n個の石を取り出したとして、その中に当たりである黒石がどれぐらい含まれているのかを示す確率分布です。

二項分布との違いは、二項分布は石を取り出すたびに一度壺の中に戻しますが、超幾何分布では戻さない点が異なります。以下のヒストグラムは、20個中当たり10個外れ10個が入っている壺から5個取り出すということを、10000回繰り返した時に含まれている当たりの数の分布です。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.hypergeometric(10, 10, 5, 10000)
plt.hist(r, bins=20, range=(1, 6))
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

NumPyでは、超幾何分布の乱数配列の作成は、hypergeometricメソッドで行います。

hypergeometric

hypergeometricメソッドは、第一引数に当たりの数、第二引数に外れの数、第三引数に取り出す数、第四引数に作成する乱数配列の形状を渡します。例えば、以下のコードは100個中3個が当たり97個が外れの中から10個取り出した時の、含まれている当たりの数の乱数です。

import numpy as np
rng = np.random.default_rng()
rng.hypergeometric(3, 97, 10, (5,))

array([0, 0, 0, 1, 0])

このメソッドには、これ以外にオプション引数はありません。以下のページでも解説しています。

• 『Generator.hypergeometric – 超幾何分布から乱数配列を作成する方法』

多変量超幾何分布

多変量超幾何分布は、超幾何分布を一般化したものです。簡単に言うと、壺の中に三つ以上の変数、例えば、白・黒・青などの異なる石がN個入っているとして、そこから石をn個取り出した場合に、それぞれの石がどのぐらい含まれているかを表す確率分布です（一度取り出した石は壺に戻さない）。

NumPyでは、この多変量超幾何分布の乱数配列の作成は、multicariate_hypergeometricメソッドで行います。

multivariate_hypergeometric

multivariate_hypergeometricメソッドでは、第一引数に壺の中に入っている各種石の数、第二引数にそのツボの中から取り出す標本のかず、第三引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.multivariate_hypergeometric((10, 10, 10), 5, 5)

array([[3, 1, 1],
       [3, 1, 1],
       [1, 2, 2],
       [1, 2, 2],
       [1, 2, 2]])

このコードでは、それぞれの種類の石が10個ずつ合計30個入った壺から5個取り出すとして、その内訳の乱数が作成されています。

これを10000回行ったとしたら、それぞれの分布は以下のようになります。

import matplotlib.pyplot as plt
import numpy as np

rng = np.random.default_rng()
s = rng.multivariate_hypergeometric((10, 10, 10), 5, 10000)
plt.hist(s)
plt.show()

さらに詳しくは、以下のページで解説しています。

• 『Generator.multivariate_hypergeometric – 多変量超幾何分布から乱数配列を作成する方法』

2.3. ポアソン分布

ポアソン分布は、起こる確率が一定のあるランダムな事象が、一定期間内に何回発生するかを示す離散確率分布です。例えば以下のコードは、ある一定期間に3回発生する事象が、100000回の一定時間の間に何回発生するかを表したヒストグラムです。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.poisson(3, 100000)
plt.hist(r, bins=50, range=(0, 10))
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

NumPyでは、このポアソン分布から乱数配列を作成するためにpoissonメソッドが用意されています。

poisson

poissonメソッドは、第一引数に一定期間における発生回数(確率密度関数におけるλ)、第二引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.poisson(10, 5)

array([11,  8, 11, 14, 16])

より詳しくは『Generator.poisson – ポアソン分布から乱数配列を作成する方法』で解説しています。

2.4. ジップ分布

ジップ分布（ジフ分布）は、ゼータ分布としても知られる離散確率分布です。出現頻度が k 番目に大きい要素が全体に占める割合は1/kに比例するというジップの法則を満たす分布として有名です。

以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.zipf(2, (10000))
plt.hist(s, bins=30, range=(0, 50), density=True)
plt.show()

NumPyでは、ジップ分布から乱数配列を作成する方法として、zipfメソッドが用意されています。

zipf

zipfメソッドは、第一引数に確率密度関数におけるパラメータα、第二引数に作成する乱数配列の形状を渡します。確率密度関数は以下の通りです。分母の記号はリーマンゼータ関数です。

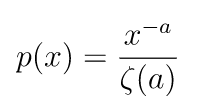
import numpy as np
rng = np.random.default_rng()
rng.zipf(2, (5, ))

array([ 8,  1,  1,  1, 16])

より詳しくは『Generator.zipf – ジップ分布から乱数配列を作成する方法』で解説しています。

3. 連続確率分布

ここでは、主に連続確率分布の乱数配列を作成するメソッドを見ていきます(1つ離散確率分布のものが混じっています）。

ここで解説するのは、様々な自然現象や経済・金融現象のパターンとよく合致することが知られている確率分布です。そのため、これらの確率分布は、基本的に現実問題のモデル化のために使われます。

それでは、一つつずつ見ていきましょう。

3.1. 指数分布の乱数配列

指数分布は、ポアソン分布に従うあるランダムな事象の発生間隔を示す確率分布です。

例えば、機械が故障してから次に故障するまでの期間・災害が起こってから次に起こるまでの期間・タクシーが通ってから次のタクシーが通るまでの時間などを表します。

以下のような確率分布を示します。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.exponential(scale=1.0, size=10000)
plt.hist(r, bins=30)
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

連続確率分布なので、作成される乱数配列の要素は浮動小数点数(float型)です。

NumPyには、指数分布の乱数配列を作成するメソッドが二つ用意されています。

• standard_exponential: 標準指数分布の乱数配列を作成
• exponential: 任意のλの指数分布の乱数配列を生成

standard_exponential

standard_exponentialメソッドは、λ= 1. の場合の指数分布の乱数配列を作成します。第一引数に作成する乱数配列の形状を渡すだけで使うことができます。

import numpy as np
rng = np.random.default_rng()
rng.standard_exponential((5,))

array([2.43577264, 1.4885122 , 1.133015  , 0.43504195, 0.67784424])

他に、オプション引数でデータ型や、乱数メソッド、出力先の変更などが可能です。詳しくは以下で解説しています。

• 『Generator.standard_exponential – 標準指数分布の乱数配列を作成』

exponential

exponential関数では、指数分布の確率密度関数において任意のλの値を設定できるようになっています。第一引数にβの値 (注:βはラムダの対数、つまりλ=1/β)、第二引数に作成する乱数配列の形状を渡します。

なお、指数分布の確率密度関数は以下の通りです。

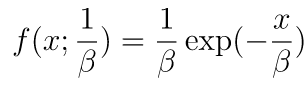
import numpy as np
rng = np.random.default_rng()
rng.exponential(4., (5,))

array([11.05435793,  4.56268099,  1.58902538,  2.22829795,  0.46032575])

詳しくは以下で解説しています。

• 『Generator.exponential – 指数分布から乱数配列を作成する方法』

3.2. ガンマ分布

ガンマ分布は、あるランダムな事象がn回起こるまでの時間の分布を示したものです。以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.gamma(1., 2., 100000)
plt.hist(r, bins=30)
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

ガンマ分布の乱数配列の作成には、以下の2つのメソッドが用意されています。

• standard_gamma: 標準指数分布の乱数配列を作成
• gamma: 任意のガンマ分布の乱数配列を生成

standard_gamma

standard_gammaメソッドは、スケール(scale)が1のガンマ分布を作成する関数です。第一引数にはガンマ分布の形状(shape)、第二引数には作成する乱数配列の形状(size)を渡します。

なお、スケール(scale)はガンマ分布の確率密度関数におけるθ、形状(shape)は確率密度関数における k です。ガンマ分布では、平均 = θ x k です。そして、k の値が大きければ大きいほど、ガンマ分布は正規分布に近づきます。

ガンマ分布の確率密度関数は以下の通りです。

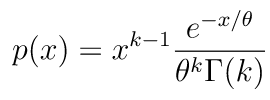
import numpy as np
rng = np.random.default_rng()
rng.standard_gamma(10000, size=(5, ))

array([ 9848.74265124,  9959.69793389,  9941.79293912, 10193.42417321,
        9822.03178008])

他にオプション引数として、dtype と out を指定することができます。より詳しくは以下のページで解説しています。

• 『Generator.standard_gamma – 標準ガンマ分布から乱数配列を作成する方法』

gamma

gammaメソッドは、形状 k とスケール θ の両方のパラメータを任意に設定することができます。第一引数に形状k、第二引数にスケールθ、第三引数には作成する乱数配列の形状(size)を渡します。

import numpy as np
rng = np.random.default_rng()
rng.gamma(2, 3, size=(5, ))

array([13.5847631 ,  8.55667476,  2.51566152,  3.371339  , 12.43513546])

より詳しくは以下のページで解説しています。

• 『Generator.gamma – ガンマ分布から乱数配列を作成する方法』

3.3. 対数分布

NumPyでは、対数分布の乱数配列を作成するメソッドが以下の2つ用意されています。

上が離散確率分布、下が連続確率分布です。

対数分布

対数分布は、種の多様性や発生モデルとよく適合する分布として頻繁に使われます。パラメータによって広がりは大きく異なりますが、次のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.logseries(.6, (10000,))
plt.hist(s, bins=30)
plt.show()

NumPyでは、対数分布の乱数作成にlogseriesメソッドが用意されています。

logseries

logseriesメソッドは第一引数に自由度、第二引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.logseries(.6, (5,))

array([4, 6, 1, 1, 1])

以下のページで詳しく解説しています。

• 『Generator.logseries – 対数分布から乱数配列を作成する方法』

対数正規分布

対数正規分布は、その名の通り、正規分布の対数分布です。収入・資産の分布や体重の分布などは、この対数正規分布に似通っていると言われています。

この確率分布は次のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.lognormal(0, 1, (10000,))
plt.hist(s, bins=30)
plt.show()

NumPyでは、対数分布の乱数作成にlognormalメソッドが用意されています。

lognormal

lognormalメソッドは、第一引数に平均、第二引数に標準偏差、第三引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.lognormal(0, 1, (5,))

array([1.38313623, 0.32564884, 1.1733369 , 1.89952587, 0.87929502])

詳しくは以下のページで解説しています。

• 『Generator.lognormal – 対数正規分布から乱数配列を作成する方法』

3.4. ガンベル分布

ガンベル分布は、極値分散の1つで、極値問題のモデル化のために使われます。昔から、洪水や最大風速・暴風雨の発生のモデル化において正規分布よりもよく適合することが知られています。

以下のヒストグラムで示しているように、正規分布よりも裾の広がりが大きいのが特徴です。この違いがあるために、正規分布よりも高い精度で実際の洪水の発生頻度を見積もることが可能なのです。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.gumbel(0, 1, (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

連続確率分布であるため、型は浮動小数点数(float型)です。

NumPyでは、ガンベル分布の乱数配列を作成する gumbelメソッドが用意されています。

gumbel

gumbelメソッドは、第一引数に平均値、第二引数に標準偏差、第三引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.gumbel(0, 1, (5,))

array([ 0.4520018 ,  1.83014722,  1.03309483, -0.34424003, -1.27420458])

より詳しくは、以下のページで解説しています。

• 『Generator.gumbel – ガンベル分布から乱数配列を作成する方法』

3.5. ワイブル分布

ワイブル分布は、ガンベル分布と同じく極値分布の一つです。例えば、製品の寿命を統計的に見積もる時によく使われます。

ワイブル分布は以下の確率密度関数で示されます。

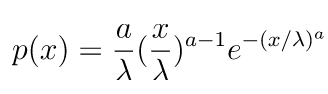
α の値が大きくなるほど形状が変わります。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
plt.subplot(131)
s = rng.weibull(1., (10000,))
plt.hist(s, bins=30, density=True)
plt.subplot(132)
s = rng.weibull(4., (10000,))
plt.hist(s, bins=30, density=True)
plt.subplot(133)
s = rng.weibull(100., (10000,))
plt.hist(s, bins=30, density=True)
plt.tight_layout()
plt.show()

ワイブル分布は連続確率分布であるため、配列の要素の型は浮動小数点数(float型)です。

NumPyでワイブル分布の乱数配列を作成するには、weibullメソッドを使います。

weibull

weibullメソッドは、第一引数に確率密度関数におけるパラメータα、第二引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.weibull(1., (5, ))

array([1.41111148, 1.56276057, 0.2771494 , 0.04276901, 0.15517728])

以下のページでより詳しく解説しています。

• 『Generator.weibull – ワイブル分布から乱数配列を作成する方法』

3.5. ロジスティック分布

ロジスティック分布も、ガンベル分布のように機能し、疫学の極値問題によく使われます。また、国際チェス連盟のイロレーティング（プレイヤー達の実力を示す相対評価の指標）に使われていることで有名です。チェスプレイヤーの成績が、ロジスティック分布とよく合致するからです。

以下のようなヒストグラムを描きます。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.logistic(0, 1., (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

ロジスティック分布は連続確率分布であり、要素の型は浮動小数点数(float型)です。NumPyでは、logisticメソッドを使って作成します。

logistic

logisticメソッドは、第一引数に平均値、第二引数に標準偏差、第三引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.logistic(0, 1, (5, ))

array([-0.335279  , -0.04664557,  0.79655963,  1.71885714,  1.34832231])

より詳しくは、以下のページで解説しています。

• 『Generator.logistic – ロジスティック分布から乱数配列を作成する方法』

3.6. ベキ分布

ベキ分布は、パレート分布と逆の確率分布です。金融・経済・自然界など、非常に様々な現象を示す分布と考えられており、例えば、過剰な保険金請求のモデル化などに使われます。

以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.power(10., (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

連続確率関数であり、乱数の型は浮動小数点数( float型)です。NumPyではベキ分布の乱数配列の作成には、powerメソッドを使います。

power

powerメソッドは、第一引数にベキ分布の確率密度関数におけるパラメータα、第二引数に作成する乱数配列の形状を渡します。ベキ分布の確率密度関数は次の通りです。

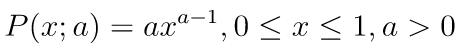
import numpy as np
rng = np.random.default_rng()
rng.power(10, (5, ))

array([0.68405776, 0.80004782, 0.84180095, 0.99323949, 0.99129558])

より詳しくは以下のページで解説しています。

• 『Generator.power – ベキ分布から乱数配列を作成する方法』

3.7. ラプラス分布

ラプラス分布は二重指数分布とも呼ばれます。正規分布と似ていますが、よりピークが鋭く、裾が広い確率分布をしています。金融工学や経済学などの分野のモデル化に適していることが知られています。

以下にヒストグラムを示しておきます。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.laplace(0, 1., (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

連続確率分布であるため、作成される配列の要素の型は浮動小数点数(float型)です。NumPyでは、このラプラス分布の乱数配列作成のためにlaplaceメソッドが用意されています。

laplace

laplaceメソッドは、第一引数に平均値、第二引数に確率密度関数におけるλ、第三引数に作成する乱数配列の形状を渡します。

なお、ラプラス関数の確率密度関数は以下の通りです。

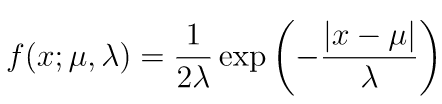
import numpy as np
rng = np.random.default_rng()
rng.laplace(0, 1, (5, ))

array([-0.73806025, -0.68755452,  0.06509857, -0.26392402,  1.00381874])

より詳しくは、以下のページで解説しています。

• 『Generator.laplace – ラプラス分布から乱数配列を作成する方法』

3.8. ワルド分布

ワルド分布は、「逆ガウス分布」としても知られています。ワイブル分布と並んで、株価収益率や利子率のモデリングによく使われる連続確率分布です。

以下のような形状をしており、広がりが大きくなればなるほど正規分布に近づいていきます。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
plt.subplot(121)
h = plt.hist(rng.wald(1, 1, 100000), bins=200, density=True)
plt.subplot(122)
h = plt.hist(rng.wald(1, 30, 100000), bins=200, density=True)
plt.tight_layout()
plt.show()

NumPyでは、このワルド分布から乱数配列を作成するメソッドとして、waldメソッドが用意されています。

wald

waldメソッドは、第一引数に平均値、第二引数に広がり(scale）、第三引数に作成する乱数配列の形状を渡します。確率密度関数は次の通りです。

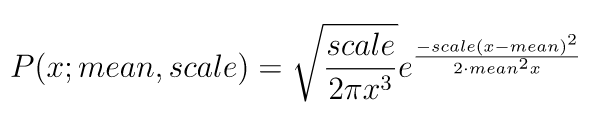
import numpy as np
rng = np.random.default_rng()
rng.wald(1, 1, (5, ))

array([0.9769615 , 0.54451718, 0.36440616, 0.72244966, 0.59640933])

詳しくは以下のページで解説しています。

• 『Generator.wald – ワルド分布から乱数配列を作成する方法』

3.9. パレート分布

パレート分布は、パレートの法則（別名「80vs20ルール」）で有名な確率分布です。よく聞くのは、業績の80%を20%の従業員が上げており、他の80%の従業員は業績の20%にしか貢献していないというルールです。パレートの法則は、それだけでなく、富の配分の分布や、保険に関する統計の分布、油田サイズの分布など、さまざまな現象を表す確率分布です。

以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.pareto(10., (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

パレート分布は連続確率分布であり、要素の型は浮動小数点数(float型)です。NumPyでは、paretoメソッドで、このパレート分布の乱数配列を作成することができます。

pareto

paretoメソッドは、第一引数に確率密度関数におけるパラメータα、第二引数に作成する乱数配列の形状を渡します。

パレート分布の確率密度関数は以下の通りです。

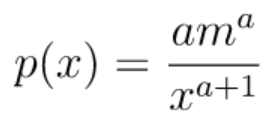
import numpy as np
rng = np.random.default_rng()
rng.pareto(10, (5, ))

array([0.02916996, 0.05964212, 0.11879227, 0.06966737, 0.08800499])

より詳しくは、以下のページで解説しています。

• 『Generator.pareto – パレート分布から乱数を作成する方法』

3.10. レイリー分布

レイリー分布は、平均波高に対するあり得る波の高さの分布や、平均風速に対するあり得る風速の分布などを示す確率分布として知られています。ワイブル分布は、このレイリー分布を一般化したものです。

以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.rayleigh(1., (10000,))
plt.hist(s, bins=30, density=True)
plt.show()

ご覧の通り、レイリー分布は連続確率分布です。NumPyでは、このレイリー分布の乱数配列を作成する方法として、rayleighメソッドが用意されています。

rayleigh

rayleighメソッドは、第一引数に最頻値かつ平均値であるscale、第二引数に作成する乱数配列の形状を渡します。なお、レイリー分布の確率密度関数は以下の通りです。

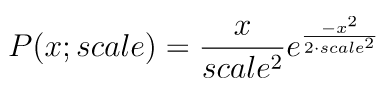
import numpy as np
rng = np.random.default_rng()
rng.rayleigh(1, (5, ))

array([2.22799372, 1.08804295, 1.01500329, 0.84376388, 1.86170415])

より詳しくは、以下のページで解説しています。

• 『Generator.rayleigh – レイリー分布から乱数配列を作成する方法』

3.11. 三角分布

三角分布は、下限値・最頻値・上限値のみが分かっている場合で、分布ははっきりしないというような問題に対して、よく便宜的に使われます。以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.triangular(-3, 0, 8, 100000)
plt.hist(s, bins=50, density=True)
plt.show()

ご覧のような連続確率分布を描きます。NumPyでは、三角分布の乱数配列の作成はtriangularメソッドで行います。

triangular

triangularメソッドは、第一引数に下限値、第二引数に最頻値、第三引数に上限値、第四引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.triangular(-3, 0, 8, (5, ))

array([-2.14101961,  0.81921086,  1.28957282, -1.03729877,  2.86972747])

より詳しくは、以下のページで解説しています。

• 『Generator.triangular – 三角分布から乱数配列を作成する方法』

3.12. ベータ分布

ベータ分布は、ベイズ推定や順序統計量においてよく見られる確率分布です。以下の確率密度関数で表され、α と β の値が大きいほど正規分布に近づき、小さいほど連続一様分布に近づきます。

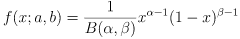
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()

plt.subplot(121)
s = rng.beta(1., 1., 10000)
plt.hist(s)

plt.subplot(122)
s = rng.beta(10., 10., 10000)
plt.hist(s, bins=30)

plt.tight_layout()
plt.show()

NumPyでは、このベータ分布から乱数配列を作成するために、betaメソッドが用意されています。

beta

betaメソッドは、第一引数に確率密度関数におけるα、第二引数にβ、第三引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.beta(1., 1., (5,))

array([0.26292855, 0.87750219, 0.66697139, 0.91209581, 0.31816716])

詳しくは以下のページで解説しています。

• 『Generator.beta – ベータ分布から乱数配列を作成する方法』

3.12. ディリクレ分布

ディリクレ分布は、ベータ分布を多変量に拡張した分布と考えることができます。わかりやすい例としてよく見られるのは、長さ1.0の紐をハサミで切って、k本の紐にするというものです。それぞれ指定の長さの3本に切るとしたら、実際の切片の長さは次のようになる傾向があります。

import matplotlib.pyplot as plt
import numpy as np

rng = np.random.default_rng()
s = rng.dirichlet((10, 5, 3), 20).transpose()

plt.barh(range(20), s[0])
plt.barh(range(20), s[1], left=s[0], color='g')
plt.barh(range(20), s[2], left=s[0]+s[1], color='r')
plt.show()

これがディリクレ分布で得られる乱数配列です。そして、NumPyには、ディリクレ分布からの乱数配列の作成のために dirichletメソッドが用意されています。

dirichlet

dirichletメソッドの第一引数には、確率密度関数におけるパラメータαを浮動小数点数のシーケンス（配列・リスト・タプルなど）で渡します。第二引数には、作成する乱数配列の形状を渡します。

ディリクレ分布の性質上、他のメソッドと比べて、戻り値は特殊です。第二引数で(m, n)と指定した場合、作成される配列の形状は、(m, n, k)になります。kはパラメータαに渡したシーケンスの長さです。

import numpy as np
rng = np.random.default_rng()
rng.dirichlet([0.1, 0.4, 1.], (5, ))

array([[4.84551746e-02, 3.14469689e-01, 6.37075137e-01],
       [9.33032178e-09, 3.11562403e-04, 9.99688428e-01],
       [2.66661860e-02, 2.68259579e-02, 9.46507856e-01],
       [2.26104854e-02, 3.15463711e-01, 6.61925804e-01],
       [7.84226837e-03, 1.65802716e-01, 8.26355016e-01]])

詳しくは以下のページで解説しています。

• 『Generator.dirichlet – ディリクレ分布から乱数配列を作成する方法』

3.13. フォン・ミーゼス分布

フォン・ミーゼス分布は、円周正規分布としても知られます。その名の通り、円周状の正規分布です。ただし、正規分布とは異なる点も多いです。方向統計学における代表的な分布モデルとして使われます。

フォン・ミーゼス分布の乱数作成のために、Numpyでは、vonmisesメソッドが用意されています。

vonmises

vonmisesメソッドは、第一引数に最頻値、第二引数に確率密度関数におけるκ、第三引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.vonmises(0, 1, (5, ))

array([-0.69171321,  0.63820832,  0.63237028,  1.81480953,  1.91608735])

より詳しくは、以下のページで解説しています。

• 『Generator.vonmises – フォン・ミーゼス分布から乱数配列を作成する方法』

4. 推定統計学に使われる確率分布

4.1. カイ二乗分布の乱数配列

カイ二乗分布には、次の2つのメソッドが用意されています。

これらは連続確率分布であり、作成する乱数配列の要素の型は浮動小数点数(float型)になります。

カイ二乗分布

カイ二乗分布は、統計検定でよく使われる分布で、期待値と実現値の食い違いを検証するものです（これを「カイ二乗検定」と言います）。

例えば、赤玉と白玉が同数入っている箱から、玉を20回取り出すとします。この場合、期待値としては赤玉と白玉は10個ずつ取り出されると計算できます。しかし、実際は赤玉11個白玉9個というように微妙にずれることが多いです。カイ二乗分布は、このずれの確率分布です。

以下のヒストグラムのように、期待値から解離した値ほど現れにくくなります。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.chisquare(1, 10000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.show()

カイ二乗分布から乱数配列を作成する関数として、NumPyにはchisquareメソッドが用意されています。

chisquare

chisquateメソッドには、第一引数に自由度、第二引数に作成する乱数配列の形状を整数（1次元配列の場合）か整数のタプル（多次元配列の場合）で渡します。

import numpy as np
rng = np.random.default_rng()
rng.chisquare(1, 5)

array([0.38783752, 1.601118  , 0.01311269, 0.55589655, 0.04936322])

詳しくは以下のページで解説しています。

• 『Generator.chisquare – カイ二乗分布から乱数配列を作成』

非心カイ二乗分布

非心カイ二乗分布は、その名の通りカイ二乗分布の中心をずらした確率分布です。非心度が小さいほどカイ二乗分布に近くなり、大きいほど正規分布に近づきます。以下のヒストグラムでご確認ください。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
plt.subplot(121)
values = plt.hist(rng.noncentral_chisquare(3, .0000001, 100000),
                  bins=200, density=True)
plt.subplot(122)
values = plt.hist(rng.noncentral_chisquare(3, 100, 100000),
                  bins=200, density=True)
plt.tight_layout()
plt.show()

NumPyでは、この非心カイ二乗分布の乱数配列の作成には、noncentral_chisquareメソッドを使います。

noncentral_chisquare

noncentral_chisquareメソッドは、第一引数に自由度、第二引数に非心度、第三引数に生成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.noncentral_chisquare(1., 20., size=(5,))

array([ 9.563788  , 25.28210068,  4.54434404, 19.36213349, 12.29268155])

詳しくは以下のページで解説しています。

• 『Generator.noncentral_chisquare – 非心カイ二乗分布から乱数配列を作成する方法』

4.2. F分布の乱数配列

F分布はF検定で帰無仮説に従う分布として用いられます。カイ二乗分布と並んで、統計学において非常に重要な分布と言えます。NumPyでは、F分布と非心F分布の二種類の乱数配列を作成するメソッドが用意されています。

これらは連続確率分布であり、作成される乱数配列の要素は浮動小数点数(float型)です。

F分布

F分布は、統計学におけるF検定で使われる重要な分布です。これは、簡潔に言うと、比較する複数の標本集団のうち、集団内の分散（自由度）と集団間の分散（自由度）の比較を行うものです。それぞれの自由度の値によって広がり方が異なりますが、以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.f(1., 5., 100000)
plt.hist(r, bins=30, range=(1, 30))
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

F分布から乱数配列を作成する方法として、NumPyには fメソッドが用意されています。

f

fメソッドは第一引数に集団間の自由度、第二引数に集団内の自由度、第三引数に作成する配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.f(1., 5., size=(5,))

array([0.36965993, 0.20045977, 1.02000951, 0.02979782, 0.51157459])

詳しくは以下のページで解説しています。

• 『Generator.f – F分布から乱数配列を作成する方法』

非心F分布

非心F分布は、以下のヒストグラムのように、F分布から中心がずれたものです。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
r = rng.noncentral_f(1., 5., 20., 100000)
plt.hist(r, bins=30, range=(1, 100))
plt.xlabel('random sample')
plt.ylabel('frequency')
plt.show()

非心F分布の乱数配列を作成する際に使うのは、noncentral_fメソッドです。

noncentral_f

noncentral_fメソッドは、第一引数に集団間の自由度、第二引数に集団内の自由度、第三匹数に非心度、第四引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.noncentral_f(1., 5., 30., size=(5,))

array([ 42.78416402, 105.40364569,  37.36876419,  40.08042965,
        51.33696406])

より詳しくは以下のページで解説しています。

• 『Generator.noncentral_f – 非心F分布から乱数配列を作成する方法』

4.3. t分布の乱数配列

t分布はt検定において用いられる重要な確率分布です。標本の平均と、実際の平均（正規分布に準ずると仮定）を比較することで、あるデータがどれだけ信用できるものかを判定するものです。

t分布は、以下のヒストグラムように自由度が高いほど、正規分布に近づいていきます。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
plt.subplot(121)
plt.hist(rng.standard_t(3, 10000), bins=30)
plt.subplot(122)
plt.hist(rng.standard_t(100, 10000), bins=30)
plt.tight_layout()
plt.show()

NumPyではt分布の乱数配列を作成するメソッドとして、standard_tメソッドが用意されています。

standard_t

standard_tメソッドは、第一引数に自由度、第二引数に作成する乱数配列の形状を渡します。

import numpy as np
rng = np.random.default_rng()
rng.standard_t(10, (5, ))

array([-1.5955715 ,  0.32153462, -0.10410117,  0.85854854, -0.34174507])

より詳しくは、以下のページで解説しています。

• 『Generator.standard_t – t分布から乱数配列を作成する方法』

4.4. コーシー分布

コーシー分布は、ガウス分布よりも裾が重い形状をしています。仮説検定の研究において有用です。以下のような形状をしています。

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
s = rng.standard_cauchy( (10000,))
plt.hist(s, bins=50, range=(-25, 25), density=True)
plt.show()

コーシー分布は連続確率分布です。NumPyでは、コーシー分布の乱数配列作成のために、standard_cauchyメソッドが用意されています。

standard_cauchy

standard_cauchyメソッドでは、引数は配列の形状のみを渡します。分布における最頻値は0.0で固定です。

import numpy as np
rng = np.random.default_rng()
rng.standard_cauchy((5, ))

array([-1.23196268, -1.48488002, -1.84738615,  0.67099457,  0.12633764])

より詳しくは、以下のページで解説しています。

• 『Generator.standard_cauchy – 標準コーシー分布の乱数配列を作成する方法』

5. まとめ

以上が乱数配列の作成のために使えるNumPyのrandomモジュールのメソッドのすべてです。冒頭でお伝えした通り、すべてを覚えておく必要はありません。ただし乱数を扱う機会がある時に、見返すようにして頂くと良いでしょう。