行列の対角化とは、ある行列の固有値を成分とした対角行列を作ることを意味します。
これはシンプルですが強力なツールであり、経済学から統計学、工学、物理学に到る様々な分野で、主に漸化式や微分方程式を効率よく解くために使われています。
そこで、このページでは、行列の対角化の方法を見ながら、対角化とは何かということを具体的に解説します。その後に行列の対角化の最も一般的な使い方である、行列のべき乗の簡単な求め方を解説します。
そして最後に、理解を深めるために役立つ練習問題を用意しています。
ぜひ、行列の対角化に対する理解を深めるために役立てて頂ければ幸いです。それでは始めましょう。
1. 対角行列とは
行列の対角化とは文字通り、行列を対角行列に変換することです。それでは対角行列とは何なのでしょうか。先にこの点について理解しておきましょう。
前回の記事『固有値と固有ベクトルとは何か？幾何学的意味と計算方法の解説』では、固有値と固有ベクトルについて解説しました。ここでは固有ベクトルが基底ベクトルであるような行列について考えてみましょう。
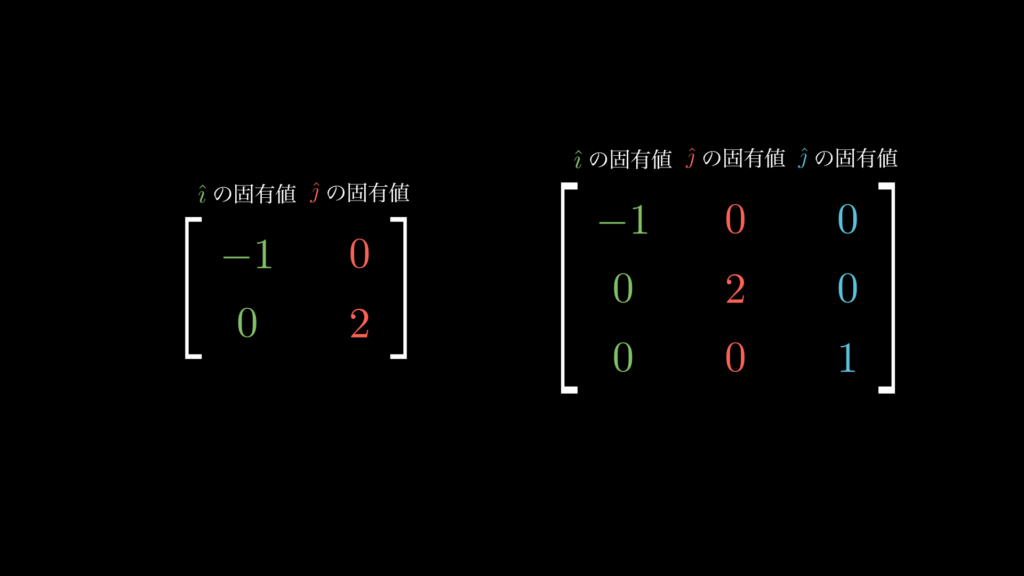
固有ベクトルとは、その行列で線形変換をしても向きが変わらないベクトルです。そして固有値はその際の倍数です。例えば、以下の線形変換をする行列は、基底ベクトル \(\hat{\imath}\) が固有値−１の固有ベクトルで、 \(\hat{\jmath}\) が固有値２の固有ベクトルです。
上のアニメーションで示していますが、このように基底ベクトルが部分空間から外れず空間を伸縮させるだけの行列は、対角線以外の成分が０になります。そのため、このような行列を「対角行列」と言います。
つまり対角行列とは、基底ベクトルが固有ベクトルであり、対角線上の値がそれぞれの基底ベクトルの固有値である行列なのです。
ポイント
対角行列とは、対角線上の成分が各基底ベクトル（＝固有ベクトル）の固有値であり、対角線上以外の成分が０の行列のこと。
2. 対角行列の意義
さて、それでは対角行列にはどのような意義があるのでしょうか。結論からお伝えすると、これを使うと行列のべき乗の計算がとても楽になります。「それだけ？」と思われるかもしれませんが、冒頭でもお伝えした通り、これは経済学から統計学、工学、物理学などさまざまな分野で使われている重要な技術なのです。
この点について理解するために、まずは対角行列以外の場合を考えてみましょう。
例えば以下の行列 \(A\) があるとします。
\[\begin{eqnarray}
A=\left[\begin{array}{cc} 3 & 0 \\ 1 & 2 \end{array} \right]
\end{eqnarray}\]
この行列の１００乗を求めよ、と言われたら、以下のように行列の積を１００回も行わなければならず、とてもできるものではありません。
\[\begin{eqnarray}
A^{100}=
\underbrace{
\left[\begin{array}{cc} 3 & 0 \\ 1 & 2 \end{array} \right]
\left[\begin{array}{cc} 3 & 0 \\ 1 & 2 \end{array} \right]
\cdots
\left[\begin{array}{cc} 3 & 0 \\ 1 & 2 \end{array} \right]
}_{100回}
\end{eqnarray}\]
しかし対角行列では、この計算をはるかに簡単に行うことができます。たとえば、以下の対角行列 \(D\) があるとします。
\[\begin{eqnarray}
D=\left[\begin{array}{cc} 3 & 0 \\ 0 & 2 \end{array} \right]
\end{eqnarray}\]
この場合、べき乗の計算は次のようになります。
\[\begin{eqnarray}
D^2=\left[\begin{array}{cc} 3^2 & 0 \\ 0 & 2^2 \end{array} \right]
,\hspace{3mm}
D^3=\left[\begin{array}{cc} 3^3 & 0 \\ 0 & 2^3 \end{array} \right]
,\hspace{3mm}
D^{100}=\left[\begin{array}{cc} 3^{100} & 0 \\ 0 & 2^{100} \end{array} \right]
\end{eqnarray}\]
このように対角行列ではない行列のべき乗の計算は大変ですが、対角行列ではとても簡単にできるのです。
それでは、対角行列ではない行列 \(A\) を、対角行列に変換できるとしたらどうでしょうか。とても有り難いですね。そして、それを可能にする方法が「行列の対角化」です。
そこで、まずは行列の対角化の方法について解説してから、この計算方法を見ていくことにしましょう。
ポイント
「行列の対角化」とは、任意の行列を、便利な性質をもつ対角行列に変換すること。
3. 行列の対角化の方法
それでは行列の対角化方法を見ていきましょう。ここでは以下の３つを解説します。
- 行列の対角化の公式
- この公式の解説
- 対角化不可能な行列について
早速見ていきましょう。
3.1. 行列の対角化の公式
さて、それでは上で用いた行列 \(A=\left[\begin{array}{cc} 3 & 0 \\ 1 & 2 \end{array} \right]\) を対角化するには、どうすれば良いでしょうか。
結論からお伝えすると、以下の公式で対角化することができます。
行列の対角化の方法
\[\begin{eqnarray}
P^{-1}AP=D
\end{eqnarray}\]
\(P\) は行列 \(A\) の固有ベクトルを列ベクトルにした行列のことです。
行列 \(A\) の固有ベクトルは、\(\left[\begin{array}{c} 1 \\ 0 \end{array} \right]\) と \(\left[\begin{array}{c} -1 \\ 1 \end{array} \right]\) です。そのため、\(P=\left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right]\) です。なお、どちらの列にどちらのベクトルを入れても構いません。
また、固有ベクトルの求め方を復習したい場合は、『固有値と固有ベクトルとは何か？幾何学的意味と計算方法の解説』をご覧ください。
さて、この \(P\) を用いて、 \(A\) の対角化行列は次のように求められます。
\[\begin{eqnarray}
P^{-1}AP
=
\left[\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right]
\left[\begin{array}{cc} 3 & 1 \\ 0 & 2 \end{array} \right]
\left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right]
=
\left[\begin{array}{cc} 3 & 0 \\ 0 & 2 \end{array} \right]
\end{eqnarray}\]
3.2. 理由の解説
それでは、なぜこの方法で行列を対角化することができるのでしょうか。
繰り返しになりますが、対角行列とは固有ベクトルが基底ベクトルであり、対角線の成分が固有値（基底ベクトルの倍率）であるような行列です。
ということは、まずは行列 \(A\) の固有ベクトルが基底ベクトルになるように基底変換を行えば良いのです。
実際に \(P^{-1}AP\) の最初の行列 \(P\) は、基底ベクトルを行列 \(A\) の固有ベクトルに基底変換（＝基底ベクトルの変更）することを意味しています。つまり、基底ベクトルを \(\left[\begin{array}{c} 1 \\ 0 \end{array} \right]\) と \(\left[\begin{array}{c} 0 \\ 1 \end{array} \right]\) のペアから、\(\left[\begin{array}{c} 1 \\ 0 \end{array} \right]\) と \(\left[\begin{array}{c} -1 \\ 1 \end{array} \right]\) のペア（＝固有基底）に変えるということです。
以下のアニメーションは、この基底変換（基底変換行列による線形変換）までを示したものです。
これで基底ベクトルが、\(\left[\begin{array}{c} 1 \\ 0 \end{array} \right]\) と \(\left[\begin{array}{c} -1 \\ 1 \end{array} \right]\) のペアになりました。
次に \(A\) による線形変換は、\(P\) によって基底変換をした新しい座標系における線形変換を行うものです。これらの積 \(AP\) は、元々の基底ベクトルのペアの座標系における同じ線形変換を表しています。
つまり、\(P\) によって基底変換をした新しい座標系における行列 \(A\) は、元々の座標系における行列 \(AP\) と等しいということです。
\[\begin{eqnarray}
\overbrace{
A=\left[\begin{array}{cc} 3 & 1 \\ 0 & 2 \end{array} \right]
}^{新しい座標系における変換行列}
\hspace{3mm}
\Longleftrightarrow
\hspace{3mm}
\overbrace{
AP =\left[\begin{array}{cc} 3 & 0 \\ 0 & 2 \end{array} \right]
}^{元々の座標系において左と同じ変換をする変換行列}
\end{eqnarray}\]
ここまでを以下のアニメーションで示しています。
さて、このアニメーションを見て気づくことがあります。
行列 \(P\) で行った基底変換は、行列 \(A\) の固有ベクトルを基底ベクトルに変換するものだったので、新しい座標系で \(A\) による線形変換を行うと、新しい基底ベクトルのペアは向きが変わらずに、伸縮するだけなのです。つまり、\(A\) は新しい座標系における伸縮行列であり、\(A\) の列ベクトルは、それぞれの基底ベクトルの倍率を表す固有値であることを意味しているということです。
そうであれば、いつもの見慣れた座標系では、伸縮行列＝対角行列なので、この \(A\) を元々の座標系に基底変換すれば、対角行列が現れることになります。その方法はわかりますね。最初に行列 \(P\)で基底変換したので、元の座標系に戻すには、その逆行列 \(P^{-1}\) であらためて基底変換をすれば良いのです。
すると、以下のアニメーションで示している通り、基底ベクトル \(\hat{\imath}\) と \(\hat{\jmath}\) の倍率が対角線上に配置された伸縮行列が出来上がります。
対角行列とは、何だったかをもう一度思い出してみましょう。それは、「基底ベクトルが固有ベクトルであり、対角線上の値がそれぞれの基底ベクトルの固有値である行列」でしたね。ということは、こうして出来上がった伸縮行列こそが、行列 \(A\) を対角化した行列なのです。
以上が、\(P^{-1}AP\) で行列を対角化することができる理由です。
3.3. 対角化不可能な行列
なお、すべての行列で対角化が可能なわけではありません。上の理由解説からわかるように、ある \(n\) 次正方行列があったとして、その行列に \(n\) 本の独立した固有ベクトルがなければ対角化することはできません。
なぜなら、そうでなければ固有ベクトルを列ベクトルとした行列 \(P\) を作ったときに、その逆行列 \(P^{-1}\) を求めることができないからです。つまり、行列 \(P\) が正則行列である必要があるのです（正則行列については『正則行列とは何かがアニメーションで驚くほどよくわかる解説』で解説しています）。
もちろん、『固有値と固有ベクトルとは何か？幾何学的意味と計算方法の解説』で解説しているように、剪断行列などの固有ベクトルが \(n\) 本に満たない行列も、そもそも \(P\) を作ることができないので対角化不可能です。
なお、あくまでも行列 \(P\) が正則でなければいけないのであって、行列 \(A\) ではありませんのでご注意ください。実際、\(A\) 自体は非正則行列でも構いません。その場合は、以下のように対角線上の成分に０がある行列になります。
\[\begin{eqnarray}
A=\left[\begin{array}{cc} 1 & 2 \\ 2 & 4 \end{array} \right]
,\hspace{3mm}
P^{-1}AP
=
\left[\begin{array}{cc} -0.4 & 0.2 \\ 0.2 & 0.4 \end{array} \right]
\left[\begin{array}{cc} 1 & 2 \\ 2 & 4 \end{array} \right]
\left[\begin{array}{cc} -2 & 1 \\ 1 & 2 \end{array} \right]
=
\left[\begin{array}{cc} 0 & 0 \\ 0 & 5 \end{array} \right]
\end{eqnarray}\]
ポイント
\(n\) 次の正方行列 \(A\) に \(n\) 本の独立した固有ベクトルが存在しない場合は、その行列 \(A\) を対角化することはできない。なぜなら、その場合は行列 \(P\) が非正則になるか、そもそも正方行列 \(P\) を作ることができなくなるから。
4. 行列のべき乗計算
さて、それでは「2. 対角行列の意義」のところで残しておいた、行列 \(A\) のべき乗計算を、この行列の対角化を使って求めてみましょう。
これは次のように求めることができます。
\[\begin{eqnarray}
A^{n}=PD^{n}P^{-1}
\end{eqnarray}\]
簡単に解説すると \(D=P^{-1}AP\) であり、この式における \(P\) と \(P^{-1}\) は固有基底に変換するための行列に過ぎないので、\(D^n=P^{-1}A^nP\) となることは少し考えればわかると思います。
そして以下のように、この式の両辺の左側に \(P\) 右側に \(P^{-1}\) を掛けると上の公式が導き出されます。
\[\begin{eqnarray}
& & PD^nP^{-1}=PP^{-1}A^nPP^{-1} \\
&\rightarrow& PD^nP^{-1}=A^n
\end{eqnarray}\]
例えば、ここまで用いてきた \(A=\left[\begin{array}{cc} 3 & 1 \\ 0 & 2 \end{array} \right]\) の１００乗を求める場合は、次の計算だけで求めることができます。
\[\begin{eqnarray}
A^{100}
&=&
PD^{100}P^{-1}\\
&=&
\left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right]
\left[\begin{array}{cc} 3^{100} & 0 \\ 0 & 2^{100} \end{array} \right]
\left[\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right]
\end{eqnarray}\]
はるかに簡単になりましたね。
対角行列の応用例
ここでは上で解説した「行列のべき乗が遥かに楽になる」という対角化行列の特性を活用した応用例を見てみましょう。ここは少し難しいかもしれないので、必ずしも理解できなくても大丈夫です。行列の対角化は、こういう風に使われているんだということを知っていただければ十分です。
行列の対角化は、様々な分野で使われている重要な概念です。その一つに、たとえばフィボナッチ数列から求められる黄金比というものがあります。
フィボナッチ数列は次のような数列です。
\[
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, \cdots
\]
この数列の \(n\) 番目の数字は次のようにして求められています。
\[
f_{n+1} = f_{n} + f_{n-1}
\]
たとえば、\(5\)番目の数字は \(f_5 = 3 + 2 = 5\) ですし、\(8\)番目の数字は \(f_8 = 13 + 8 = 21\) です。これを順番に求めていくことで、フィボナッチ数列はできあがります。
この数列は、多くの面白い性質を持っていることで有名です。たとえば…
\[
\frac{1}{1}=1,\hspace{3mm} \frac{2}{1}=2,\hspace{3mm} \frac{3}{2}=1.5,\hspace{3mm} \frac{5}{3}=1.666…
\]
というように隣り合う数字の比を求めてみます。そうすると次のようになります。
\[
1, 2, 1.5, 1.666…, 1.6, 1.625, 1.615…, 1.619…, 1.618…, 1.61818…, 1.618…
\]
こうして見てみると、下図のように 1.618…辺りの値に収束していっていることがわかります。
それでは、最終的にどの値に収束しているのでしょうか。これは行列の対角化によって解くことが可能なのです。
先ほども見た通り \(f_{n+1} = f_{n} + f_{n-1}\) でしたね。そして、当たり前ですが \(f_n = f_n\) です。ということは、これは次のように連立方程式で表すことができます。
\[
\begin{cases}
1f_{n} + 1f_{n-1 }= f_{n+1} \\
1f_n + 0f_{n-1 } = f_n
\end{cases}
\]
これを「行列の連立方程式」で表すと、以下のようになりますね。
\[
\left( \begin{array}{c} f_{n+1} \\ f_n \end{array} \right)
=
\left( \begin{array}{c} f_{n}+f_{n−1} \\ f_n \end{array} \right)
=
\left( \begin{array}{c} 1 & 1 \\ 1 & 0 \end{array} \right)
\left( \begin{array}{c} f_n \\ f_{n−1} \end{array} \right)
\]
ここで、それぞれ次のように置き換えるとします。
\[
A = \left( \begin{array}{c} 1 & 1 \\ 1 & 0 \end{array} \right),
\hspace{3mm}
V_n = \left( \begin{array}{c} f_{n+1} \\ f_n \end{array} \right)
\]
そうすると上の式は以下のように表現することができます。
\[
V_n = A^1V_{n-1} = A^2V_{n-2} = \cdots =A^nV_0
\]
なお、\(V_0\) は数列の最初なので…
\[
V_0 = \left( \begin{array}{c} f_1 \\ f_0 \end{array} \right)
= \left( \begin{array}{c} 1 \\ 1 \end{array} \right)
\]
です。
さて、ここで \(V_n\) を求めることが収束値を求めることになります。
普通に求めると、たとえば \(V_5\) は…
\[\begin{eqnarray}
V_5 = A^5V_0 & = &
\left( \begin{array}{c} 1 & 1 \\ 1 & 0 \end{array} \right)^5
\left( \begin{array}{c} 1 \\ 1 \end{array} \right) \\
& = &
\left( \begin{array}{c} 8 & 5 \\ 5 & 3 \end{array} \right)
\left( \begin{array}{c} 1 \\ 1 \end{array} \right) \\
& = &
\left( \begin{array}{c} 13 \\ 8 \end{array} \right)
\end{eqnarray}\]
となりますが、そうではなく、まず行列 \(A\) を対角化します。
そのために\(A\) の固有値と固有ベクトルを求めます。固有値を \(\lambda\) とすると固有方程式は…
\[
|A−\lambda E| =
\left| \begin{array}{c} 1−\lambda & 1 \\ 1 & −\lambda \end{array} \right|
= 0
\]
となります。途中の計算は省きますが、これの固有値 \(\lambda\) の値は以下の通りになります。
\[
\lambda_+ = \dfrac{1+\sqrt{5}}{2}, \hspace{3mm} \lambda_− = \dfrac{1-\sqrt{5}}{2}
\]
そして、それぞれの固有値に対する固有ベクトルは以下の通りです。
\[\begin{eqnarray}
\lambda_+ &\rightarrow& \left( \begin{array}{c} \lambda_+ \\ 1 \end{array} \right),
\hspace{4mm}
\lambda_− &\rightarrow& \left( \begin{array}{c} \lambda_− \\ 1 \end{array} \right)
\end{eqnarray}\]
ということは、この場合の行列 \(A\) の対角化行列は次の通りです。
\[
D=P^{−1}AP =
\left( \begin{array}{cc} \lambda_+ & 0 \\ 0 & \lambda_− \end{array} \right)
\]
さて、もともと求めたかったのは、\(\vec{V}_n\) の成分比である…
\[
\dfrac{f_{n+1}}{f_n}
\]
で、\(n\) を限りなく大きくした場合の値でしたね。
そして、これは…
\[
V_n = A^nV_0
\]
で求めますから、計算するには行列 \(A\) を限りなく何回も掛けることが必要になります。こういう時こそ、\(A^n=PDP^{−1}\) の出番です。
\(A_n\) は次のように計算することができます。
\[\begin{eqnarray}
A^{n} &=& PDP^{−1} \\
&=&
\left( \begin{array}{c} \lambda_+ & \lambda_− \\ 1 & 1 \end{array} \right)
\left( \begin{array}{cc} \lambda_+{}^n & 0 \\ 0 & \lambda_−{}^n \end{array} \right)
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc} 1 & −\lambda_− \\ −1 & \lambda_+ \end{array} \right)\\
&=&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc} \lambda_+{}^{n+1} & \lambda_−{}^{n+1} \\ \lambda_+{}^{n} & \lambda_−{}^n \end{array} \right)
\left( \begin{array}{cc} 1 & \frac{1}{\lambda_+} \\ −1 & \frac{1}{\lambda_−} \end{array} \right)\\
&=&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+1} − \lambda_−{}^{n+1}
& \lambda_+{}^{n} − \lambda_−{}^{n}\\
\lambda_+{}^{n} − \lambda_−{}^{n}
& \lambda_+{}^{n−1} − \lambda_−{}^{n−1}
\end{array} \right)\\
\end{eqnarray}\]
そして、\(V_n\) は次のように計算することができます。
\[\begin{eqnarray}
V^{n} &=& A^nV_0 \\
&=&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+1} − \lambda_−{}^{n+1}
& \lambda_+{}^{n} − \lambda_−{}^{n}\\
\lambda_+{}^{n} − \lambda_−{}^{n}
& \lambda_+{}^{n−1} − \lambda_−{}^{n−1}
\end{array} \right)
\left( \begin{array}{c} 1 \\ 1 \end{array} \right)
\\
&=&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+1} − \lambda_−{}^{n+1}
+ \lambda_+{}^{n} − \lambda_−{}^{n}\\
\lambda_+{}^{n} − \lambda_−{}^{n}
+ \lambda_+{}^{n−1} − \lambda_−{}^{n−1}
\end{array} \right)\\
&=&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+2}−\lambda_−{}^{n+2}\\
\lambda_+{}^{n+1}−\lambda_−{}^{n+1}
\end{array} \right)
\end{eqnarray}\]
さて、これで \(V_n\) を求めることができました。このようにフィボナッチ数列の一般項は、行列 \(A\) を対角化することによって得られるのですね。
それでは、実際に黄金比の極限値を求めてみましょう。まず、この場合は、限りなく大きい \(n\) に対して…
\[
\lim_{n \to \infty} \lambda_−{}^n = 0
\]
となります。つまり、\(n\) が非常に大きい場合は \(\lambda_−\) の項は無視することができるので…
\[\begin{eqnarray}
V_n &= &
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+2}−\lambda_−{}^{n+2}\\
\lambda_+{}^{n+1}−\lambda_−{}^{n+1}
\end{array} \right)\\
&\rightarrow&
\dfrac{1}{\sqrt{5}}
\left( \begin{array}{cc}
\lambda_+{}^{n+2}\\
\lambda_+{}^{n+1}
\end{array} \right)
\end{eqnarray}\]
と考えて良いことになります。
ということは…
\[\begin{eqnarray}
\dfrac{f_{n+1}}{f_n}
=
\dfrac{\lambda_+{}^{n+2}}{\lambda_+{}^{n+1}}
=
\lambda_+
=
\dfrac{1+\sqrt{5}}{2}
\end{eqnarray}\]
になります。
このように行列 \(A\) を対角化することによって、\(A^n\) を簡単に計算することができるのです。これが黄金比の求められ方です。
なおこの方法は、ここまで見てきたような漸化式を解くためだけでなく、微分方程式を解くためにも有効で、良く使われています。
5. 練習問題
ここでは最後に行列の対角化についての理解を深めるために、練習問題を用意しておきます。ぜひ一度は解いてみてください。
6. まとめ
最後に重要なポイントをまとめておきましょう。
まず行列の対角化は次のようにして行うことができます。
- 行列の固有値と固有ベクトルを求める。
- 固有ベクトルを重ねた行列 \(P\) を作る。
- 上で重ねた固有ベクトルに対応する固有値を、順番通りに対角上に配置した対角行列を作る。
行列の対角化の公式は次の通りです。
行列の対角化の公式
\[P^{−1}AP = D\]
続いて、対角化行列を用いて、行列のべき乗を簡単に計算する方法は以下の通りです。
行列のべき乗の公式
\[A^n = PD^nP^{−1}\]
練習問題を解くことが、これらの理解の助けになりますので、ぜひチャレンジしておいて頂ければと思います。
コメント
コメント一覧 （2件）
とても参考になりました。
一点だけ確認させていただきたいことがあります。
3.2章の「理由の解説」における、行列Aの定義が変わっているのですが、A={{3,0},{1,2}}でしょうか、それともA={{3,1},{0,2}}でしょうか？
線形代数の勉強でお世話になってます。線形代数の抽象論でつまずいておりましたが、アニメーションで幾何的に理解することで、より理解が進んでおります。ありがとうございます。
3.1. 行列の対角化の公式の説明で、行列Aの固有ベクトルを求めていますが、当初示された行列Aは
(3 0
1 2)
でしたが、固有ベクトルの計算の時から
(3 1
0 2
になってませんでしょうか？