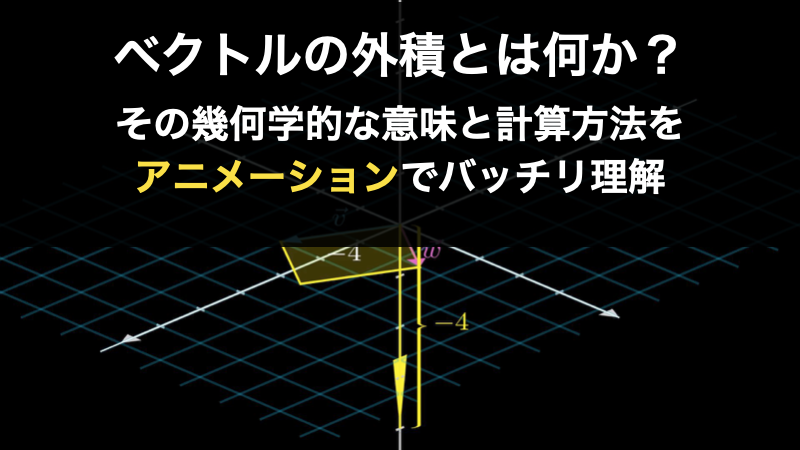
ベクトルの外積とは、「2本のベクトルが作る平行四辺形に対して、垂直な方向に働く新しいベクトル」のことです。そして、ベクトル \(\vec{v}\) と \(\vec{w}\) があるとき、外積は \(\vec{v}\times \vec{w}\) と表すので、「クロス積」とも言います。
このベクトルの外積は、線形代数において幅広く使われる重要な概念です。そのため、これについての理解を深めることで、線形代数の幾何学的なイメージをさらにグッと深めることができて、さまざまな面での応用力が身に付きます。
そのためにも、このページでは、ベクトルの外積について誰でも正しく理解できるようになるために、幾何学的なアニメーションを豊富に用いながら徹底的に解説してきます。きっとお役に立つことでしょう。
それでは始めます。
1.ベクトルの外積の幾何学的な意味
それでは、このベクトルの外積とはどのようなものなのでしょうか。まずは、これの幾何学的な意味を確認しましょう。早速、以下のアニメーションをご確認ください。2つのベクトル \(\vec{v}\) と \(\vec{w}\) の外積を示しているものです。
このように、ベクトルの外積 \(\vec{v}\times\vec{w}\) とは、2つのベクトル \(\vec{v}\) と \(\vec{w}\) が作る平行四辺形に対して垂直方向に伸びる新しいベクトルなのです。つまり、ベクトルの外積の解はベクトルです。そして、この新しいベクトルの長さは、2つのベクトルが作る平行四辺形の面積と等しくなります。
なお、垂直方向というと、平行四辺形に対して真上の方向と真下の方向という2つの可能性があります。このうちどちらの方向に伸びるのかは、有名な「右手の法則」で判断することが可能です。具体的には \(\vec{v}\) を人差し指、\(\vec{w}\) を中指としたら、外積 \(\vec{v}\times\vec{w}\) の方向は親指の方向になります。
ぜひ以下のアニメーションでご確認ください。
以上がベクトルの外積の幾何学的な意味です。繰り返すと、ベクトルの外積とは、2つのベクトルが作る平行四辺形に対して垂直方向に伸びる新しいベクトルです。
ポイント
・ベクトルの外積とは2つのベクトルが作る平行四辺形に対して垂直に伸びる新しいベクトル(つまり両方のベクトルと同時に垂直に伸びている)。
・ベクトルの外積の長さは2つのベクトルが作る平行四辺形の面積に等しい。
2. ベクトルの外積の計算方法
ベクトルの外積の幾何学的な意味を理解したところで、次にその求め方について見ていきましょう。
ここでは、そのための公式と、なぜこの公式でベクトルの外積が求められるのかを幾何学的に詳しく解説します。これらを理解することで、線形代数に使われるさまざまな概念の理解を飛躍的に深めることができます。そのためにもぜひ真剣に読み進めて見てください。
2.1. ベクトルの外積の公式
まずはベクトルの外積の座標の求め方からお伝えします。これは以下の公式で求めることができます。
ベクトルの外積の座標の求め方の公式
\[
\vec{v}\times\vec{w}=
\left[ \begin{array}{cc} v_1 \\ v_2 \\ v_3 \end{array} \right]
\times
\left[ \begin{array}{cc} w_1 \\ w_2 \\ w_3 \end{array} \right]
=
\left[ \begin{array}{cc}
v_2w_3-w_2v_3 \\
-v_1w_3+w_1v_3 \\
v_1w_2-w_1v_2
\end{array} \right]
\]
公式から外積を求められる理由①
なぜこの方法でベクトルの外積を求めることができるのでしょうか?
実は、これは以下のように基底ベクトル \(\hat{\imath}\)、\(\hat{\jmath}\) 、\(\hat{k}\) を1列目の要素に、ベクトル \(\vec{v}\)、\(\vec{w}\) をそれぞれ2列目と3列目の要素にした3次行列式を解くという計算になっています。そして、この行列式を解くと、上の公式が導き出されます。
なお行列式については『行列式とは?意味と定義と求め方~行列式とは何か驚くほどよくわかる解説~』で解説しています。また、以降の内容は『余因子による行列式の展開とは?~アニメーションですぐわかる解説~』の理解も必要です。復習したい方はぜひご覧ください。
\[\begin{eqnarray}
\vec{v}\times\vec{w}
&=&
\left[ \begin{array}{cc} v_1 \\ v_2 \\ v_3 \end{array} \right]
\times
\left[ \begin{array}{cc} w_1 \\ w_2 \\ w_3 \end{array} \right]
=
\mathrm{det}
\left(
\left[ \begin{array}{cc}
\hat{\imath} & v_1 & w_1 \\
\hat{\jmath} & v_2 & w_2 \\
\hat{k} & v_3 & w_3 \\
\end{array} \right]
\right)
\end{eqnarray}\]
それでは、このように行列式の要素に基底ベクトル \(\hat{\imath}\)、\(\hat{\jmath}\)、\(\hat{k}\)を加えるのにはどのような意味があるのでしょうか。この点について一緒に考えてみましょう。
まずは以下のアニメーションをご覧ください。これは上の行列式の計算がどのようなものなのかを表しています。
このアニメーションが表していることを文字で解説したものが以下です。
まず、この行列式の \((v_2w_3-w_2v_3)\hat{\imath}\) の前半部分は横軸を\(y\) 軸、縦軸を \(z\) 軸とした平面上において、\(\vec{v}\) と \(\vec{w}\) が作る平行四辺形の面積です。そして、面積とベクトルの外積の長さは等しいため、この面積に基底ベクトル \(\hat{\imath}\) を掛けたベクトルは、ベクトルの外積の \(x\) 軸成分と等しくなります。
同じように、\(-(v_1w_3+w_1v_3)\hat{\jmath}\) は横軸を\(x\) 軸、縦軸を \(z\) 軸とした平面上において、\(\vec{v}\) と \(\vec{w}\) が作る平行四辺形の面積です。これに基底ベクトル \(\hat{\jmath}\) を掛けると、ベクトルの外積の \(y\) 軸成分と等しくなります。
\((v_1w_2-w_1v_2)\hat{k}\) の部分も同様です。横軸を\(x\) 軸、縦軸を \(y\) 軸とした平面上において、\(\vec{v}\) と \(\vec{w}\) が作る平行四辺形の面積と、基底ベクトル \(\hat{k}\) を掛けるものなので、これはベクトルの外積の \(z\) 軸成分と等しくなります。
以上のことから、これら3つを足し合わせたものがベクトルの外積と等しくなるのです。
公式から外積を求められる理由②
さて、もう少し深く考えてみましょう。
\(\vec{v}\) と \(\vec{w}\) に加えて、以下の2つのベクトル \(\vec{p}\) と \(\vec{x}\) 、さらに \(\vec{x}\)、\(\vec{v}\)、\(\vec{w}\) を列ベクトルとした行列式 \(\mathrm{det}A\) 使って解説します。
\[\begin{eqnarray}
\vec{p}
&=&
\left[ \begin{array}{cc} p_1 \\ p_2 \\ p_3 \end{array} \right]
,\hspace{3mm}
\vec{x}&=&
\left[ \begin{array}{cc} x \\ y \\ z \end{array} \right],\hspace{3mm}
\mathrm{det}A
=
\mathrm{det}
\left(
\left[ \begin{array}{cc}
x& v_1 & w_1 \\
y & v_2 & w_2 \\
z & v_3 & w_3 \\
\end{array} \right]
\right)
\end{eqnarray}\]
これらを使うと面白いことがわかります。それは、ベクトルの外積を求めるということは、幾何学的には、内積 \(\vec{p}\cdot\vec{x}\) と行列式 \(\mathrm{det}A\) の値が同じになるようなベクトル \(\vec{p}\) を求めることと同じであるというものです。
これを式にしたものが以下です。
なおベクトルの内積については『ベクトルの内積とは?その幾何学的な意味と計算方法を徹底解説』をご確認ください。
\[\begin{eqnarray}
\left[ \begin{array}{cc} p_1 \\ p_2 \\ p_3 \end{array} \right]
\cdot
\left[ \begin{array}{cc} x \\ y \\ z \end{array} \right]
=
\mathrm{det}
\left(
\left[ \begin{array}{cc}
x& v_1 & w_1 \\
y & v_2 & w_2 \\
z & v_3 & w_3 \\
\end{array} \right]
\right)
\tag{1}
\end{eqnarray}\]
さて、これは一体どういうことなのでしょうか。
わかりやすくするために、ここからは、\(\vec{x}=
\left[ \begin{array}{cc} -1 \\ 1 \\ 2 \end{array} \right]\)、\(\vec{v}=
\left[ \begin{array}{cc} 2 \\ 0 \\ 0 \end{array} \right]\)、\(\vec{w}=
\left[ \begin{array}{cc} 0 \\ -2 \\ 0 \end{array} \right]\) とします。なお、これらはどのようなベクトルでも構いません。
まず、ベクトルの内積 \(\vec{p}\cdot\vec{x}\)は以下のアニメーションで示しているように、\(\vec{p}\) に射影した \(\vec{x}\) の長さと \(\vec{p}\) の長さの積です(\(\vec{p}\) が黄色、 \(\vec{x}\) が白、\(\vec{v}\) が青、\(\vec{w}\) がピンク)。
次に3次行列式 \(\mathrm{det}A\) は、3本のベクトル \(\vec{x}\)、\(\vec{v}\)、\(\vec{w}\) が作る平行六面体の体積です。これは \(\vec{v}\) と \(\vec{w}\) が作る平行四辺形の面積に対して、\(\vec{x}\) のうち平行四辺形に垂直な成分(つまり \(\vec{x}\) の \(\vec{p}\) に対する射影)を掛けることで求めることができます。
以下のアニメーションでご確認ください(\(\vec{v}\times\vec{w}\) が黄色、 \(\vec{x}\) が白、\(\vec{v}\) が青、\(\vec{w}\) がピンク)。
さて、このときベクトル \(\vec{v}\) と \(\vec{w}\) が作る平行四辺形の面積は、その外積 \(\vec{v}\times\vec{w}\) の長さと等しくなります。つまり、\(\vec{p}=\vec{v}\times\vec{w}\) であれば、内積 \(\vec{p}\cdot\vec{x}\) と行列式 \(\mathrm{det}A\) が等しいことになり、\((1)\) 式を満たすのです。
以上のことから、先ほど述べた通り、ベクトルの外積を求めるということは、内積 \(\vec{p}\cdot\vec{x}\) と行列式 \(\mathrm{det}A\) の値が同じになるようなベクトル \(\vec{p}\) を求めることと同じであるということになるのです。
公式から外積を求められる理由③
さて、それでは \((1)\) 式の条件を満たすようなベクトル \(\vec{p}\) はどのようにしたら求められるのでしょうか。もうわかりますね。ベクトル\(\vec{x}\) の各要素を、基底ベクトル \(\hat{\imath}\)、\(\hat{\jmath}\) 、\(\hat{k}\) に置き換えれば良いのです。
\[\begin{eqnarray}
\left[ \begin{array}{cc} p_1 \\ p_2 \\ p_3 \end{array} \right]
\cdot
\left[ \begin{array}{cc} \hat{\imath} \\ \hat{\jmath} \\ \hat{k} \end{array} \right]
=
\mathrm{det}
\left(
\left[ \begin{array}{cc}
\hat{\imath}& v_1 & w_1 \\
\hat{\jmath} & v_2 & w_2 \\
\hat{k} & v_3 & w_3 \\
\end{array} \right]
\right)
\tag{2}
\end{eqnarray}\]
この \((2)\) 式を計算すると次のようになります。
\[\begin{eqnarray}
p_1\hat{\imath}+p_2\hat{\jmath}+p_3\hat{k} = (v_2w_3-w_2v_3)\hat{\imath}-(v_1w_3+w_1v_3)\hat{\jmath}+(v_1w_2-w_1v_2)\hat{k}\
\tag{3}
\end{eqnarray}\]
この \((3)\) 式から、\(p_1=(v_2w_3-w_2v_3)\)、\(p_2=-(v_1w_3+w_1v_3)\)、\(p_3=(v_1w_2-w_1v_2)\) となります。
以上が公式からベクトルの外積を求められる理由です。
長くなりましたが、こうやって幾何学的に見ることで、ベクトルの外積の公式には、線形代数のさまざまな事柄に対する理解を深めるための材料が盛りだくさんであることがわかったのではないでしょうか。こうした深い理解は、線形代数を実際に活用する際にとても役に立つことになります。
2.2. ベクトルの外積の長さ
念のため、ベクトルの外積の長さの計算方法についても触れておきましょう。これは、シンプルに三平方の定理を使って次のように求めます。
ベクトルの外積の長さの求め方
\[
\sqrt{(v_2w_3-w_2v_3)^2+{-(v_1w_3+w_1v_3)}^2+(v_1w_2-w_1v_2)^2}
\]
ここまで読まれた方にとっては、これについての解説は不要でしょう。なお、繰り返し触れてきましたが、ベクトルの外積の長さと、2つのベクトルが作る平行四辺形の面積は同じなので、この方法によって平行四辺形の面積を求めることもできます。この点は覚えておきましょう。
3. 覚えておきたいベクトルの外積の性質
さて、ベクトルの外積には、いくつか知っておくべき性質があります。最後にそうした性質を抑えておきましょう。なお、これらの性質は、「ある2つのベクトルの外積は、そのベクトルが作る平行四辺形の面積に等しい」ということを覚えておけば、幾何学的なイメージが容易になります。
それではそれぞれ解説していきます。
3.1. \(\vec{v}\times\vec{w}=-\vec{w}\times\vec{v}\)
まずベクトルの外積は、ベクトルの内積と違って、掛ける順番が異なると、平行四辺形の面積の符号が逆になり、新しいベクトルが伸びる方向が反対になるという性質があります。
これを式で表したものが以下です。
ベクトルの外積の性質①
\[
\vec{v}\times\vec{w}=-\vec{w}\times\vec{v}
\]
以下のアニメーションで確認してみましょう。
具体的には、 \(\vec{v}\) が \(\vec{w}\) よりも右側にある場合は、面積の符号は正になり、新しいベクトルは上方向に伸びます。反対に \(\vec{v}\) が \(\vec{w}\) よりも左側にある場合は、面積の符号は負になり、新しいベクトルは下方向に伸びます。
以下のアニメーションでご確認ください。
このように面積の符号は、ベクトルの外積が伸びる方向を表していると理解すると良いです。
なお、より厳密には \(\vec{v}\) を\(\hat{\imath}\)、\(\vec{w}\) を\(\hat{\jmath}\) と考え、\(\hat{\jmath}\) が \(\hat{\imath}\) を追い越している場合に面積は負の値になり、新しいベクトルは下方向に伸びます。これについては、『行列式とは?意味と定義と求め方~行列式とは何か驚くほどよくわかる解説~』をあらためて確認して頂くと理解しやすくなります。
また、ベクトルの内積は掛ける順番が変わっても値は同じなので混同しないように注意しましょう。両者の意味を幾何学的に理解しておけば、混同することはなくなります。『ベクトルの内積とは?その幾何学的な意味と計算方法を徹底解説』をご覧ください。
3.2. \(s\vec{v}\times\vec{w}=s(\vec{v}\times\vec{w})\)
ベクトル \(\vec{v}\) と \(\vec{w}\) の外積 \(\vec{v}\times\vec{w}\) において、一方のベクトルが \(s\) 倍になると、その外積も \(s\) 倍になります。
具体的には、\(s_1\vec{v}\times\vec{w} = s_1(\vec{v}\times\vec{w})\) ですし、\(\vec{v}\times s_2\vec{w} = s_2(\vec{v}\times\vec{w})\) です。また一方が \(s_1\) 倍になり、他方が \(s_2\) 倍になると、外積は \(s_1s_2\) 倍になります。つまり、\(s_1\vec{v}\times s_2\vec{w} = (s_1s_2)(\vec{v}\times\vec{w})\) です。
このことは以下のアニメーションをご覧頂くと、苦もなく直感的に理解することができます(外積は2本のベクトルの面積に等しいことを意識してご覧ください)。
なおベクトルのスカラー倍(定数倍)については『ベクトルの掛け算とは何か?幾何学的な意味と計算方法の解説』で解説しています。
3.3. 平行するベクトルの外積はゼロ
最後に、平行なベクトル同士では外積の値はゼロになります。理由は簡単です。2つのベクトルが平行の場合は平行四辺形を作ることができず、その面積がゼロになるからです。
反対に2つのベクトルが直交している場合は、平行四辺形の面積が最大になるため、外積の長さも最大になります。
これも以下のアニメーションで幾何学的に確認すると簡単に理解できます。
4. まとめ
いかがだったでしょうか?以上がベクトルの外積です。
教科書などでは、ベクトルの外積は線形代数の最初の方で学びます。しかし、ここまで解説してきたように、これは、線形代数のさまざまな概念を先に知っておくことで、やっと深く理解できるものです。そして、そうして得られた深い理解こそ、実務面で役に立ちます。
このページが、そうした深い理解のためのきっかけになったとしたら、とても嬉しく思います。





コメント