「線形代数を簡単に理解できるようになりたい…」。そう思ったことはないでしょうか。当ページはまさにそのような人のためのものです。ここでは線形代数の基礎のすべてを、誰でもすぐに、そして直感的に理解できるように、文章だけでなく、以下のような幾何学的なアニメーションを豊富に使って解説しています。ぜひご覧になってみてください（音は出ませんので安心してご覧ください）。
いかがでしょうか。これから線形代数の基礎概念のすべてを、このようなアニメーションとともに解説していきます。
線形代数の参考書の多くは、難しい数式がたくさん出てきて、見るだけで挫折してしまいそうになります。しかし線形代数は本来とてもシンプルです。だからこそ、これだけ多くの分野で活用されています。そして、このシンプルな線形代数の概念の数々は、アニメーションで視覚的に確認することで、驚くほどすんなりと理解することができます。
実際のところ、線形代数を活用できるようになるためには、計算方法よりもむしろ幾何学的な理解の方がはるかに重要です。そもそも今の時代、計算はコンピューターがあっという間にでやってくれるからです。
そこで、当ページでは線形代数の重要な基礎概念の一つひとつを、幾何学のアニメーションを使って（もちろん文章も使って）丁寧に解説していきます。数式や計算も出てきますが、必要十分かつ最低限に留めているので、挫折することはないと思います。そして、最後にはPythonで線形代数の基本的な演算を行う方法についても解説します。
すべて読み終わるころには、例えば機械学習やディープラーニングなどでよく出てくる「線形◯◯」や「◯◯処理」、「◯◯変換」などを理解するための土台が形成されていることでしょう。またコンピューター・グラフィックスなどの一部の分野では、そのまますぐに活用することもできます。
当ページを線形代数の理解を深めるための入り口としてお使い頂けたら、とても嬉しく思います。
1. ベクトル Part1
ベクトルは線形代数の土台の中心となっている重要な概念です。
ざっくりと言うと線形代数とは、現実世界のさまざまな現象をベクトル空間へと抽象化し、その抽象空間の中でさまざまな解析や分析を行うというものです。面白いことに、そこでの発見が、多くの場合、現実世界で役に立つのです。そのため線形代数はベクトルに始まりベクトルに終わると言っても過言ではありません。
そこで、まずはベクトルの基礎をしっかりと抑えていきましょう。以下のアニメーションは、この１章で学ぶことになる概念をダイジェストで示しているものです。何を学ぶのかが具体的にイメージできるので、ぜひご覧ください。
これらの概念をしっかりと理解することがここでの目的です。
先ほどもお伝えした通り、ベクトルは以降の概念を理解する上での土台となりますので、一つずつじっくりと学んでいきましょう。
それぞれの内容は、以下で示している８つのページに分けて解説しています。画像の下の青字のリンクをクリックすると解説ページへアクセスすることができます。ぜひ順番にご確認ください。
ベクトルについて理解する
1.1.ベクトルとは
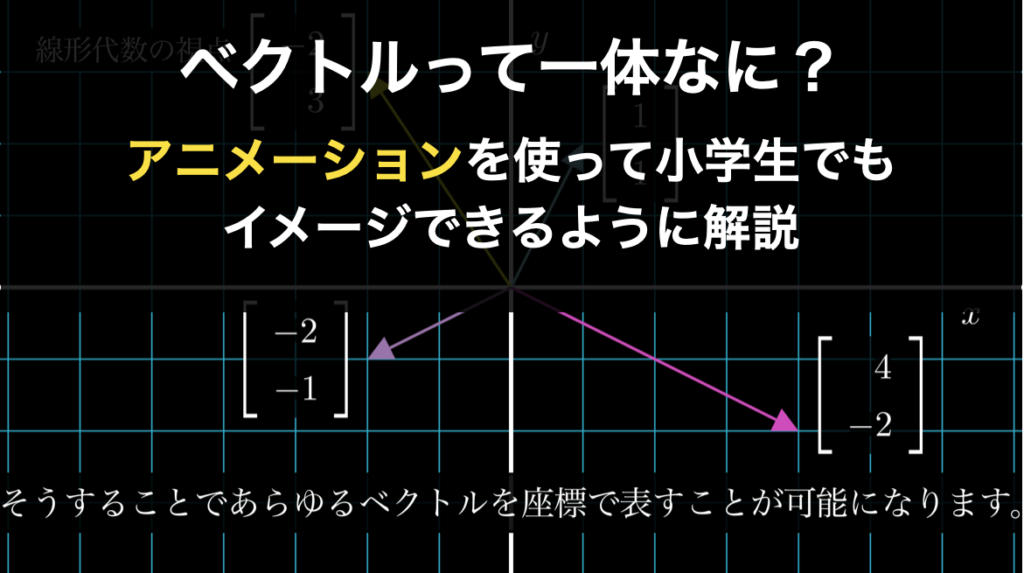
義務教育では、ベクトルは長さと向きをもつ矢印と教わります。しかしベクトルは本当は、もっともっと便利な概念です。線形代数においてベクトルとは何なのか。ぜひご確認ください。
1.2.座標系
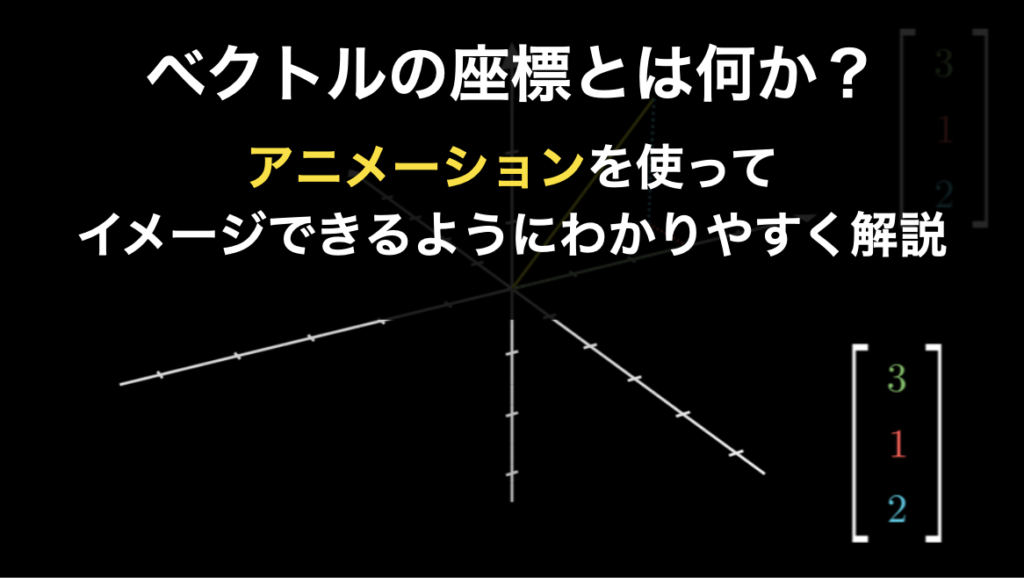
「座標系とベクトル」
線形代数では、ベクトルは座標系に存在するものであり、そのお尻は常に原点に接しているものと考えます。それでは座標系とは何で、どういう意味があるのでしょうか。ぜひご確認ください。
1.3.ベクトルの和
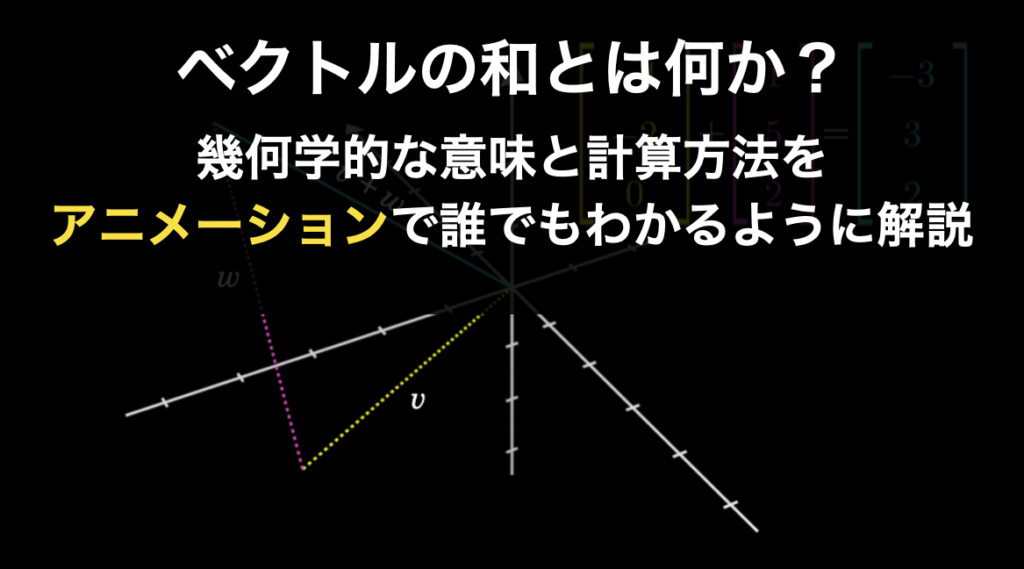
「ベクトルの和」
ベクトルの和は、ベクトルの掛け算と並んで、線形代数の核となる重要な概念の一つです。それではベクトルの和とは一体なんなのでしょうか。これを幾何学的にばっちり理解しましょう。
1.4.ベクトルの掛け算
「ベクトルの掛け算」
ベクトルの掛け算は、ベクトルの和と並んで、線形代数の核となる重要な概念の一つです。それではベクトルの掛け算とは一体なんなのでしょうか。これを幾何学的にばっちり理解しましょう。
1.5.ベクトルの分解
「ベクトルの分解」
ベクトルの和とベクトルの掛け算は、まさにこのベクトルの分解を行うための道具です。そして、ベクトルの分解は後の線形結合や線形変換を理解するための重要な概念です。ぜひご確認ください。
1.6.基底ベクトル
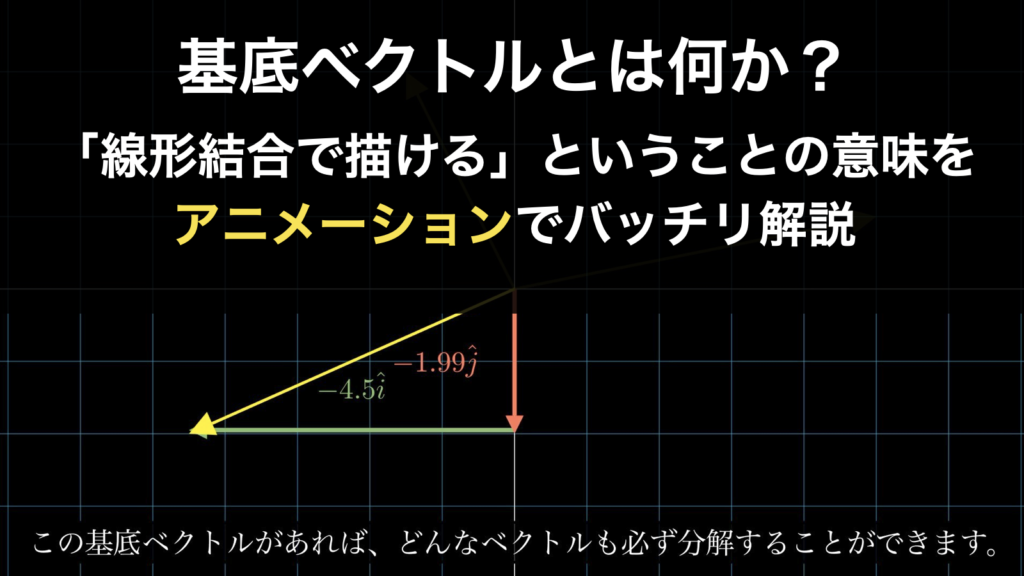
「基底ベクトル」
基底ベクトルは、線形結合・線形変換・逆行列・固有値・固有ベクトルなどのさまざまな重要概念を理解するためのカギとなります。それでは基底ベクトルとは何なのでしょうか。ぜひご確認ください。
2. 行列
続いて、行列について学びましょう。ここでは線形代数で最も面白いテーマの一つである「線形変換」も出てきます。
行列の計算は義務教育でも学んできましたが、それにどのような意味があるのかはよくわからなかったと思います。しかし、線形代数を学ぶと行列の計算が何なのかがとてもよくわかるようになります。それがわかれば、面倒だった計算も面白く感じてくるようになります。
さて、この２章で学ぶことになる主な概念を以下のアニメーションで示していますので、まずはご確認ください。
このように行列を使うことで、ベクトル空間がさまざまな変化をするようになります。これらについて、しっかりと理解するのがこの章の目的です。
それでは以下の７つのページを順番にご確認ください。画像の下の青字のリンクをクリックすると解説ページへアクセスすることができます。
行列と線形変換について理解する
2.1.行列の基礎
「行列の基礎」
行列について覚えていない方も多いと思います。そこでまずは行列の基本概念である行・列・サイズ・次元などを解説します。そして、行列とは一体何なのかということを誰でもわかるように解説しています。
2.2.行列とベクトルの積
線形代数では、ベクトルと行列の積は、ある入力値（原因）を出力値（結果）に変換するという意味があります。これを知ると、行列についての理解も大きく進みます。ぜひご覧ください。
2.3.線形変換
「線形変換」
線形変換は線形代数のもっとも面白い概念の一つです。ここから線形代数がどんどん楽しくなっていくことでしょう。線形変換とはなんなのか、アニメーションで幾何学的に解説しています。
2.4.行列と行列の積
「行列と行列の積」
行列と行列の積は、幾何学的には空間を続けて線形変換すること（ある処理を行った後に別の処理を行うこと）を意味します。このことから、これは写像の合成とも言われます。これもアニメーションで幾何学的に確認すると、すぐに理解できます。
2.5.行列の計算まとめ
「行列の計算まとめ」
ここでは行列の計算について、線形代数において重要なものを改めて解説しています。また、ここまでは正方行列のみを扱ってきましたが、ここで非正方行列の積についても触れます。これらは幾何学的に見るととても面白いです。
2.6.行列と連立方程式
「行列と連立方程式」
ここでは後の逆行列の準備として、行列を使った連立方程式の解き方を解説しています。具体的には、線形代数の教科書でよく目にする掃き出し法（ガウスの消去法）というものです。これは以後使うものなので、ぜひご確認ください。
2.7.行列の基本変形
「行列の基本変形」
ここでは掃き出し法で行う３つの基本操作である行列の基本変形について詳しく解説しています。ご覧頂くと、「行列の操作にはこうした幾何学的な意味があるのか」ということを発見できます。ぜひご覧ください。
3. 行列式
行列式は、行列による線形変換によって空間がどのように変化するのかを示す値です。具体的には、以下のアニメーションで示しているように空間の面積や体積の拡張倍率を示します。
この行列式は、すでに解説したベクトルの一次独立（線形独立）や、後で解説する逆行列・ベクトルの内積外積などとも関係する重要な概念です。３章では、以下の３つのページで、この行列式について学びましょう。
ただし、余因子展開と行列式の計算まとめについては、当ページの第一目標である「線形代数の概念を幾何学的に理解する」という観点から見て、必須ではありません。余因子展開は、サイズの大きな行列式を手計算したり、いくつかの線形代数の公式を導き出す時に使うものであり、幾何学というよりは純粋な数学に近いからです。そのため、もし難しいと感じるようなら飛ばしてしまってください。
行列式について理解する
3.1.行列式とは
「行列式とは」
ここでは行列式とは何かということを、誰でもわかるようにアニメーションで幾何学的に解説しています。そして、押さえておきたい行列式の性質も解説しています。ぜひご確認ください。
3.2.余因子展開
「余因子展開」
余因子展開（別名「ラプラス展開」は、大きな行列式を、より次元が小さな行列式の和で表すというテクニックです。これを知っておくと、大きなサイズの行列式の計算が楽になります。また様々な公式も、この余因子展開で導き出されています。
3.3.行列式の計算まとめ
「行列式の計算」
ここでは行列式の計算方法を改めて解説しています。余因子展開を学んでいれば、４次元以上の行列式も手計算できるようになりますが、それについても解説しています。ぜひご確認ください。
4. 逆行列
逆行列とは、ある行列で線形変換した空間を、元の空間に戻す行列のことです。まずは以下のアニメーションを見て、幾何学的なイメージを掴みましょう。
この逆行列は線形代数において非常に重要な役割を担っています。たとえば行列とベクトルの掛け算は入力値（原因）から出力値（結果）を導き出すものですが、逆行列を使うと、反対に出力値（結果）から入力値（原因）を導き出すということが可能になります。
またさまざまな分野で便利なツールとして使われている固有値・固有ベクトルを導き出す際にも欠かせません。
それでは以下の５つのページを見て逆行列についての理解を深めていきましょう。
5. ベクトル Part2
通常の線形代数の教科書では、ベクトルの内積と外積はもっと早い段階で出てくるのが普通です。しかし実はこれらの概念は、ここまで学んできた線形代数の知識を踏まえた上で眺めた方が、より深く理解することができます。
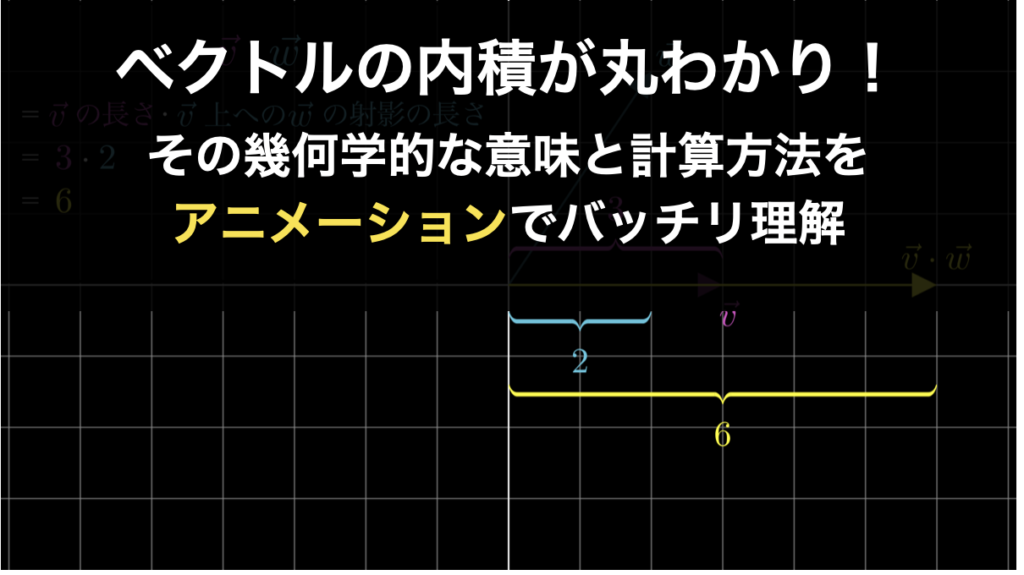
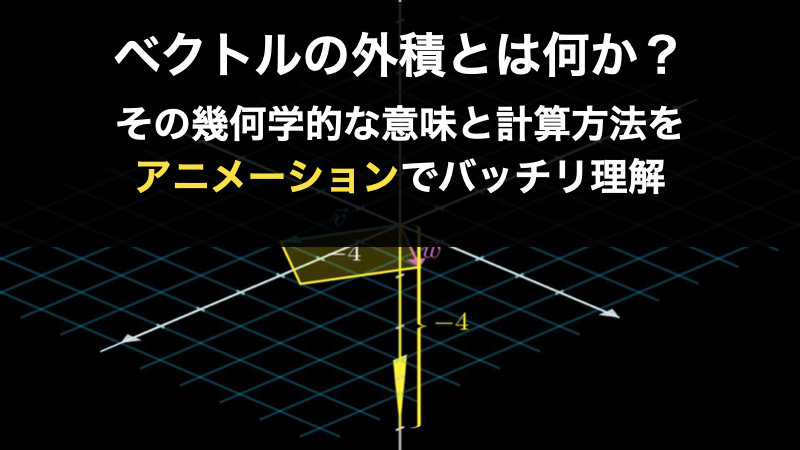
そのようなわけで、ベクトルの内積と外積についてここで解説します。これらは以下のアニメーションで示している通り、幾何学的には１次元への射影であり、２つのベクトルに対して垂直に伸びる新しいベクトルのことです。
これらの概念は特に物理学で非常に重宝されているのですが、それだけでなく線形代数における、これまでの内容の理解を深めるためにも非常に役に立ちます。以下の二つのページでじっくりと解説していますので、ぜひご確認ください。
6. 固有値と固有ベクトル
固有値と固有ベクトルは、さまざまな学問分野で計算や処理のツールとして使われている重要な概念です。これは以下のアニメーションで示しているように、線形変換をしても部分空間から外れないベクトルのことであり、固有値はその際の倍率です。
これらは、ほんの一例ですが、Google 創業時の論文にも、Webページを評価するページランクの計算に出てきます。そのような創造的な利用方法の発想を目指すのは現実的ではありませんが、線形代数を使いこなせるようになることのメリットが感じられます。
さて、固有値と固有ベクトルについては、以下の３つのページをご覧ください。なおジョルダン標準形は必須ではありませんので、難しそうなら飛ばして頂いて構いません。
固有値と固有ベクトルについて理解する
6.3.ジョルダン標準形
「ジョルダン標準形」
対角化できない行列でもジョルダン標準形という形に変換することは可能です。これによって、対角行列と同じようにべき乗の計算を楽にすることができます。必須ではありませんが、興味があればご確認ください。
7. Pythonで線形代数
それでは最後に、ここまでで学んだ線形代数の基礎概念の演算をPythonで行う方法について触れておきます。Pythonでは、科学技術計算やデータエンジニアリングにおいてはNumPyというライブラリを使うのが一般的です。NumPyは高速に動作するため、大規模な計算に適しているからです。
ぜひ以下の８つのページをご覧ください。これらのページでPythonで線形代数を行うための基礎力を身につけることができます。
Pythonで線形代数
8.まとめ
最後までご覧いただきありがとうございます。以上が線形代数の土台であり基本です。以降は、これらの知識を元にして、それぞれの専門分野の学習へと役立てて頂ければ嬉しく思います。
また、もし、
- 漏れているトピックがある
- 他に知りたいというトピックがある
- 間違えがある
という場合は、ぜひコメント欄や問い合わせフォームなどからお伝え頂ければ助かります。
なおアニメーションはpythonのmanimceライブラリで作成しています。もともと作成されたのは3b1bのGrant Sandersonさんです。彼と、manimceライブラリの開発に携わっておられるエンジニア達に感謝します。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント
コメント一覧 （1件）
線形変換の説明辺りで回転行列の符号が間違っていますよ