ベクトルの分解とは、簡単に言うと「任意のベクトルを、基準となる2本のベクトルの掛け算と和で表すこと」です。
こう聞くと、「なぜわざわざそんな面倒なことをするのか?」と疑問に思うかもしれません。しかしベクトルの分解は線形代数において非常に重要なコンセプトです。なぜならこれは「線型結合」や「ベクトルの独立」といった概念を理解するための基礎となるからです。
そのため是非ここでベクトルの分解についてしっかりと理解しておきましょう。なお理解を確認するための簡単な練習問題もありますので、ぜひあわせてご活用ください。
前提知識(ベクトルの和と掛け算について)
ベクトルの分解について理解するには、土台としてベクトルの和とベクトルの掛け算の知識を身につけておく必要があります。それぞれ『ベクトルの和とは何か?誰でもわかる幾何学的な意味と計算方法の解説』と『ベクトルの掛け算とは何か?幾何学的な意味と計算方法の解説』で解説していますので、ぜひ確認しておいてください。
1. ベクトルの分解とは
まずは以下の1分29秒のアニメーションを、ぜひご覧ください。ベクトルの分解というものを視覚的に理解することができます。
以上がベクトルの分解です。
念のため文字でも解説して起きます。内容は上のアニメーション解説と同じですが、確認のためにご覧いただくと良いでしょう。
2次元ベクトルの分解
まず以下のベクトル \(\vec{v}\) があるとします。
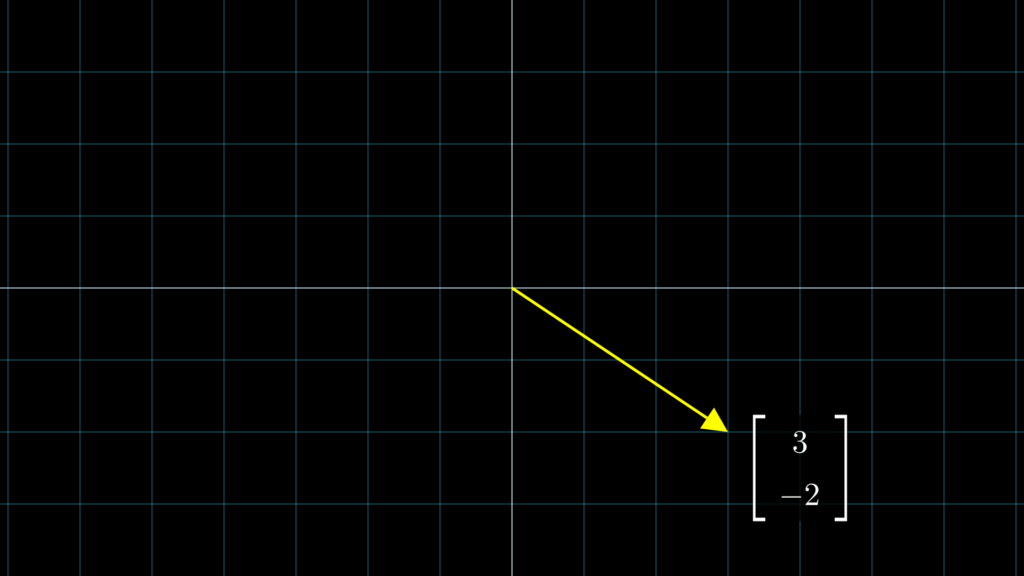
このベクトル \(\vec{v}\) の各座標は、それぞれ長さが\(1\)の水平ベクトル \(\hat{\imath}\) (アイハット) と垂直ベクトル \(\hat{\jmath}\) (ジェイハット) の掛け算と和で求めることができます。
\[\begin{eqnarray}
\hat{\imath}=
\left[ \begin{array}{c} 1 \\ 0 \end{array} \right],
\hspace{3mm}
\hat{\jmath}=
\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\end{eqnarray}\]
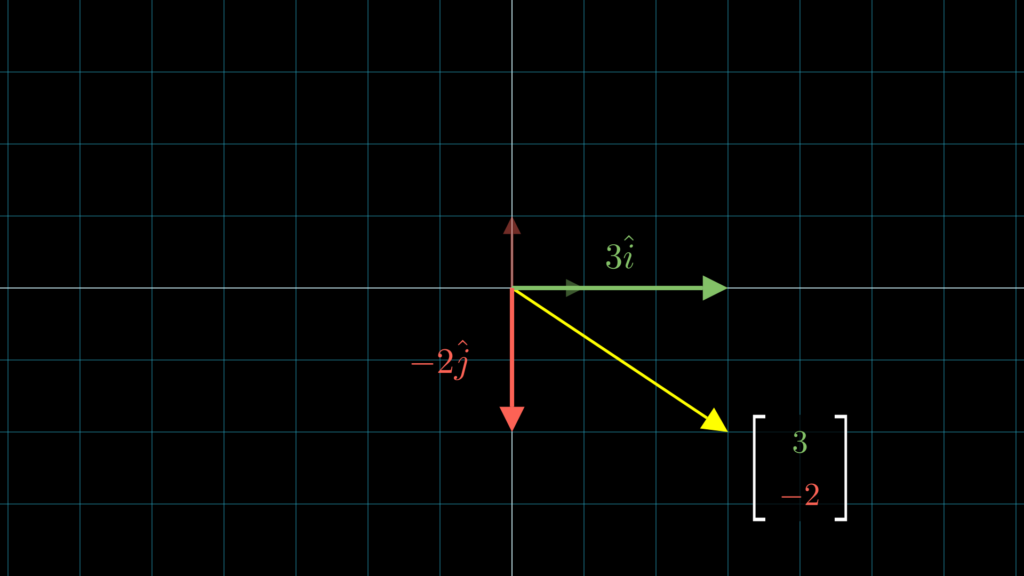
まず、ベクトル \(\vec{v}\) の \(x\) 座標は \(\hat{\imath}\) を \(3\)倍するスカラーであり、\(y\) 座標は \(\hat{\jmath}\) を \(-2\)倍するスカラーであると考えることができます。(ベクトルの掛け算(スカラー倍)については『ベクトルの掛け算とは何か?幾何学的な意味と計算方法の解説』で解説しています)。
\[\begin{eqnarray}
3\hat{\imath}=
\left[ \begin{array}{c} 3 \\ 0 \end{array} \right],
\hspace{3mm}
-2\hat{\jmath}=
\left[ \begin{array}{c} 0 \\ -2 \end{array} \right]
\end{eqnarray}\]
そして、ベクトル \(\vec{v}\) はこうしてスカラー倍した \(3\hat{\imath}\) と \(-2\hat{\jmath}\) の和で表すことができます(ベクトルの和については『ベクトルの和とは何か?誰でもわかる幾何学的な意味と計算方法の解説』をご確認ください)。
\[\begin{eqnarray}
\vec{v}=(3)\hat{\imath}+(-2)\hat{\jmath}=
\left[ \begin{array}{c} 3 \\ 0 \end{array} \right]
+
\left[ \begin{array}{c} 0 \\ -2 \end{array} \right]
=
\left[ \begin{array}{c} 3 \\ -2 \end{array} \right]
\end{eqnarray}\]
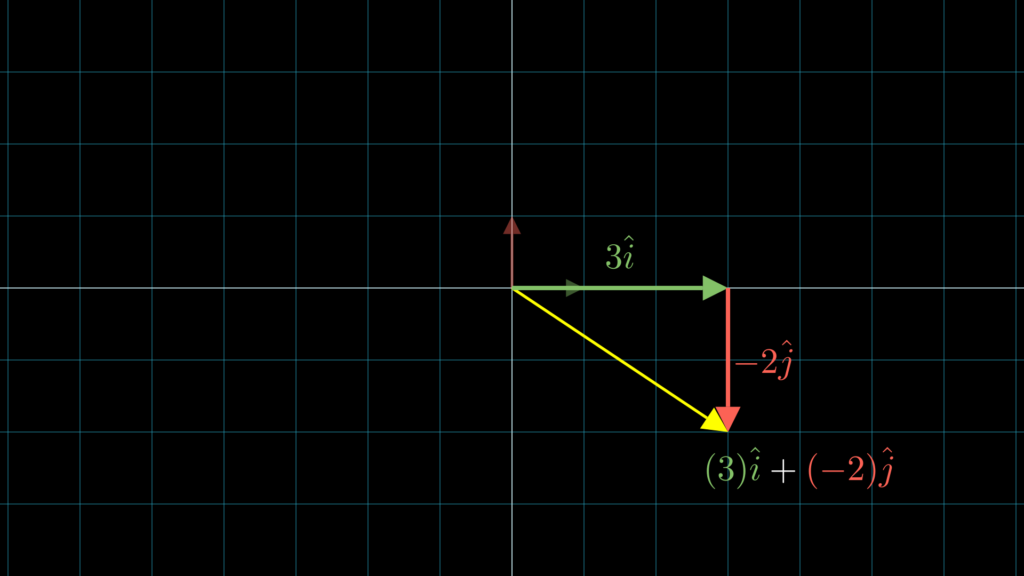
このようにベクトル \(\vec{v}\) を、「 \(\vec{v}=(3)\hat{\imath}+(-2)\hat{\jmath}\)」にするのがベクトルの分解です。
3次元ベクトルの分解
次に以下の3次元ベクトル \(\vec{v}\) を分解してみましょう。
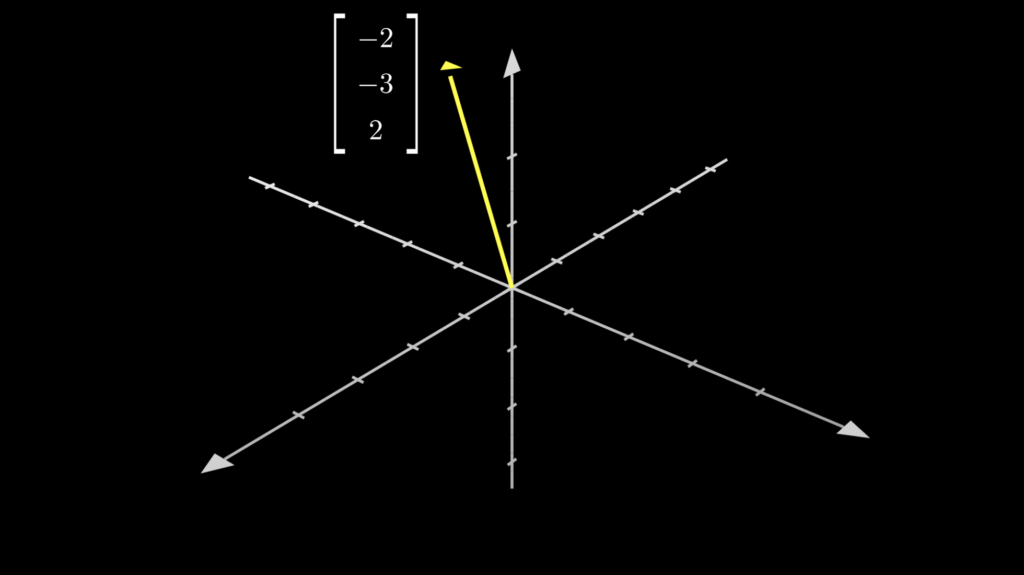
2次元ベクトルの分解では2つのベクトル \(\hat{\imath}\) と \(\hat{\jmath}\) を使いましたが、3次元ベクトルではもう1つ \(\hat{k}\) が必要になります。
\[\begin{eqnarray}
\hat{\imath}=
\left[ \begin{array}{c} 1 \\ 0 \\0 \end{array} \right],
\hspace{3mm}
\hat{\jmath}=
\left[ \begin{array}{c} 0 \\ 1 \\0\end{array} \right],
\hspace{3mm}
\hat{k}=
\left[ \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right]
\end{eqnarray}\]
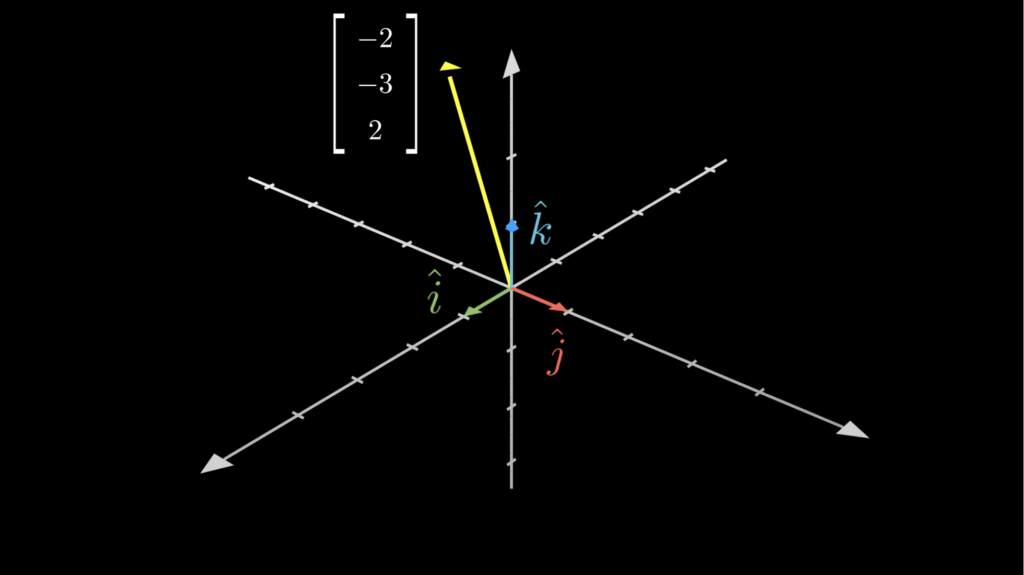
この3つのベクトルがあるとしたら、ベクトル \(\vec{v}\) の \(x\) 座標は \(\hat{\imath}\) を \(-2\) 倍するスカラーであり、\(y\) 座標は \(\hat{\jmath}\) を \(-3\) 倍するスカラーであり、\(z\) 座標は \(\hat{k}\) を \(2\) 倍するスカラーであると考えることができます。
\[\begin{eqnarray}
-2\hat{\imath}=
\left[ \begin{array}{c} -2 \\ 0 \\0 \end{array} \right],
\hspace{3mm}
-3\hat{\jmath}=
\left[ \begin{array}{c} 0 \\ -3 \\0\end{array} \right],
\hspace{3mm}
2\hat{k}=
\left[ \begin{array}{c} 0\\ 0 \\ 2 \end{array} \right]
\end{eqnarray}\]
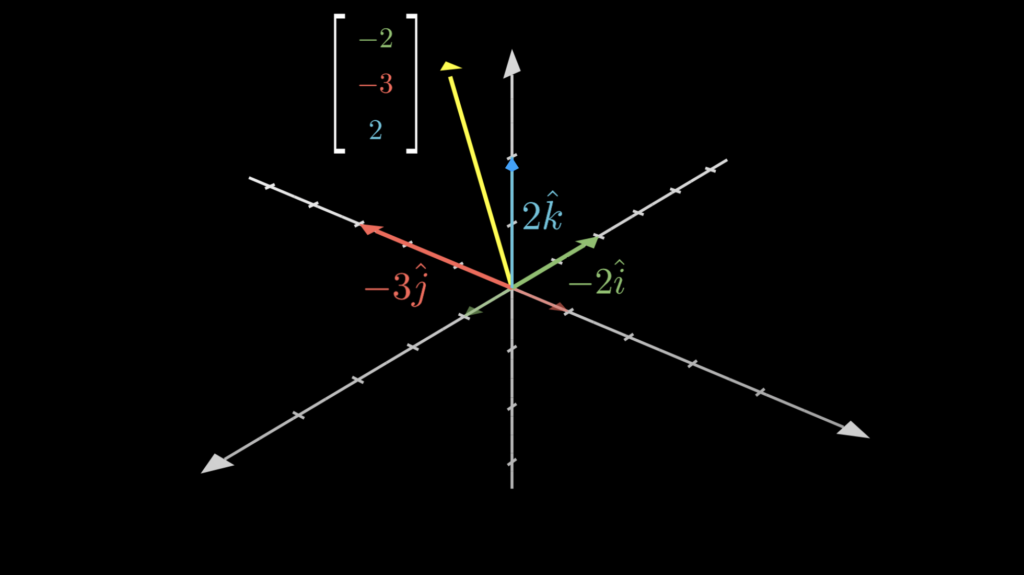
そして、ベクトル \(\vec{v}\) はこうしてスカラー倍した \(-2\hat{\imath}\) と \(-3\hat{\jmath}\) と \(2\hat{k}\) の和で表すことができます。
\[\begin{eqnarray}
\vec{v}=(-2)\hat{\imath}+(-3)\hat{\jmath}+2\hat{k}
=
\left[ \begin{array}{c} -2 \\ 0 \\0 \end{array} \right]
+
\left[ \begin{array}{c} 0 \\ -3 \\0\end{array} \right]
+
\left[ \begin{array}{c} 0\\ 0 \\ 2 \end{array} \right]
=
\left[ \begin{array}{c} -2\\ -3 \\ 2 \end{array} \right]
\end{eqnarray}\]
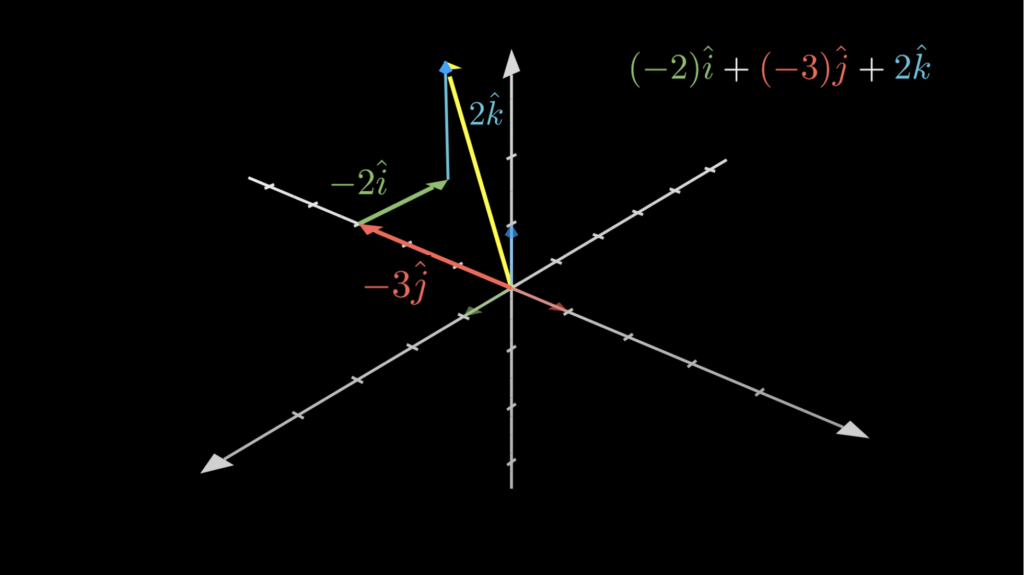
このように、この3次元ベクトル \(\vec{v}\) は「\(\vec{v}=(-2)\hat{\imath}+(-3)\hat{\jmath}+2\hat{k}\)」と分解することができます。
2. 練習問題
2次元ベクトルと3次元ベクトルの分解について、練習問題を用意しておきますので、ぜひ一度は解いてみてください。
3. まとめ
以上がベクトルの分解です。とても単純ですが、これから線形代数の学習を進めていく上で非常に重要な基礎となる知識です。しっかりと抑えておきましょう。
次に読みたい記事
当記事のアニメーションの中で、ベクトルの分解に用いた2本のベクトル \(\hat{\imath}\) と \(\hat{\jmath}\) のことを特別なベクトルであると言いました。具体的には、これらは「基底ベクトル」と言われるものです。基底ベクトルを理解することによって、線形代数において、数値を見ただけで空間をイメージできるようになっていきます。次の記事、『基底ベクトルとは何か?アニメーションで一目で理解』では、これについて解説していますので、是非ご覧ください。









コメント
コメント一覧 (2件)
線形代数を学ぶ上で大変有用なサイトをありがとうございます。
ところで、三次元ベクトルの分解①の解答が誤ってるように見えます。
基底ベクトルiのスカラーは3ではなく2ではないでしょうか?
あと、”^i”の読み方は「ハットアイ」で大丈夫でしょうか?
一般的な呼称があれば教えて下さい。
田口様
ご指摘頂きありがとうございます。早速、直させて頂きました。感謝します。
さて、^iの読み方ですが、「ハットアイ」でも通じると思いますが、私は反対に「アイハット」と呼んでいます。
おそらく、こちらの呼び方の方がスムーズに通じる場合が多いのではないかと思います。