NumPyのsin関数は、サイン(正弦)を計算する関数です。
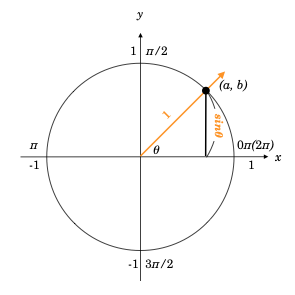
サインについて、よく使われる説明は次のようなものです。半径1の円(「単位円」といいます)があります。この円の中心から1本の光線を、角度θで放ちます。すると、この光線は円周上の点 (a, b) に接します。この時の y座標であるb が、角度がθの時のサインです。サインの値は、角度が270° (3π/2)の時の -1から、90度(π/2)の時の +1までの範囲です。そして角度180°(πの倍数)の時は 0 になります。そして πと2πの間では負の値になります。
以下の図を見ると理解が進みやすいでしょう。
そして、NumPyには、このサインに関する関数が3つあります。
- sin: ラジアンからサインの値を求める。
- arcsin: 単位円上のy座標から角度θ(sin**-1)を求める。
- sinh: 双曲線上のy座標から双曲線サイン関数の値を求める。
ここでは、これらの関数について解説します。
1. sin関数
np.sin関数は、y=sin(θ)におけるyの値を計算します。まずは書式から確認しましょう。
1.1 書式
書き方:
np.sin(x)
| 引数 | 型 | 解説 |
| x | array_like | ラジアンを要素とする配列を渡します。2πは360°です。 |
| * この他に、キーワード引数としてufunc(ユニバーサル・ファンクション)を使用可能です。具体的には、out, where, axes, axis, keepdims, casting, order, dtype, subok, signature, extobj です。しかし、これらは高度な操作を行いたい時に使うものであり、基本的には使いません。 | ||
戻り値:
| サインの値の配列 渡した配列x のそれぞれの要素ごとに計算したサインの値を要素とする新しい配列を返します。x がスカラーの場合は、戻り値もスカラー(1つの数値のみの配列)になります。 |
1.2. サンプルコード
np.sin関数には、要素をラジアンで記した配列を渡す必要があります。ラジアンでは 1° = π/180 なので、任意の角度のラジアンは 角度 * π/180 で計算することができます。
例えば、角度を表す数値が格納された配列があるとします。これをnp.sin関数に渡す際は、以下のように π/180 で乗算をしておきます。
import numpy as np
# 角度を格納した配列
x = np.array([0., 30., 45., 60., 90.])
# 角度をラジアンに変換 (np.piは円周率)
r = x * np.pi/180
# sin関数にラジアンを渡す
np.sin(r)
πは180°なので、次のような渡し方も可能です。π/2 = 90°です。
# この渡し方でも可
np.sin(np.pi/2)
お馴染みのサインカーブ(または「正弦曲線」もしくは「シヌソイド」)を描いてみましょう。
import matplotlib.pylab as plt
x = np.linspace(-np.pi, np.pi, 1000)
plt.plot(x, np.sin(x))
plt.xlabel('Angle [rad]')
plt.ylabel('sin(x)')
plt.axis('tight')
plt.show()
2. arcsin関数
arcsin関数は、単位円上(半径1の円: x2+y2=1) のy座標から角度θ(sin**-1)を求めることができる関数です。arcsinは逆三角関数におけるアークサインのことです。
書式はnp.sin関数と同じですが、np.sin関数はラジアンを渡すのに対して、np.arcsin関数は単位円上のy座標を渡します。なお、単位円上のy座標とはsinθの値のことです。
2.1. 書式
書き方:
np.arcsin(x)
| 引数 | 型 | 解説 |
| x | array_like | 単位円上のy座標を要素とする配列を渡します。必然的に値は-1~1の範囲になります。 |
| * この他に、キーワード引数としてufunc(ユニバーサル・ファンクション)を使用可能です。具体的には、out, where, axes, axis, keepdims, casting, order, dtype, subok, signature, extobj です。しかし、これらは高度な操作を行いたい時に使うものであり、基本的には使いません。 | ||
戻り値:
| 角度の配列: 渡した配列x のそれぞれの要素ごとに計算したサインの逆数を要素とする新しい配列を返します。x がスカラーの場合は、戻り値もスカラー(1つの数値のみの配列)になります。 |
2.2. サンプルコード
それではサンプルコードを見ていきましょう。
np.arcsin関数は、渡したy座標の値から、θの角度を計算しラジアンで返します。なお、単位円(円周1の円)の性質上、渡す値は-1以上1以下の範囲 である必要があります。
import numpy as np
# 単位円上のy座標が0.5の時
angle = np.arcsin(0.5)
angle
ラジアンを角度°に変換するには、円周率np.piで割って180を掛けます。
# ラジアンを角度°に変換
angle/np.pi*180
関数に配列を渡すと、それぞれの要素ごとにラジアンを計算します。
# y座標の値を格納した配列を渡す
y_cord = np.array([-1, -0.5, 0, 0.5, 1])
np.arcsin(y_cord)
# 角度°に変換
np.arcsin(y_cord)/np.pi*180
アークサインのカーブを描いてみましょう。
import matplotlib.pylab as plt
x = np.linspace(-1, 1, 1000)
plt.plot(x, np.arcsin(x))
plt.xlabel('Angle [rad]')
plt.ylabel('arcsin(x)')
plt.axis('tight')
plt.show()
3. sinh関数
sinh関数は双曲線関数における双曲線サイン関数(「シャイン」または「シンチ」)を返す関数です。双曲線サイン関数は、sinh(x) = 1/2 * (np.exp(x) – np.exp(-x)) または -1j * np.sin(1j*x) で表すことができます。なお、双曲線とは x2-y2=1 の曲線のことです。
3.1. 書式
書き方:
np.sinh(x)
| 引数 | 型 | 解説 |
| x | array_like | 双曲線上におけるy座標を要素とする配列を渡します。 |
| * この他に、キーワード引数としてufunc(ユニバーサル・ファンクション)を使用可能です。具体的には、out, where, axes, axis, keepdims, casting, order, dtype, subok, signature, extobj です。しかし、これらは高度な操作を行いたい時に使うものであり、基本的には使いません。 | ||
戻り値:
| 双曲線サイン関数の値の配列: 渡した配列x のそれぞれの要素ごとに計算した双曲線サイン関数の値を要素とする新しい配列を返します。x がスカラーの場合は、戻り値もスカラー(1つの数値のみの配列)になります。 |
3.2. サンプルコード
それではサンプルコードを見ていきましょう。
import numpy as np
np.sinh(0)
np.sinh(np.pi*1j/2)
双曲線関数のカーブを描いてみましょう。
import matplotlib.pylab as plt
x = np.linspace(-np.pi, np.pi, 1000)
plt.plot(x, np.sinh(x))
plt.xlabel('Angle [rad]')
plt.ylabel('sinh(x)')
plt.axis('tight')
plt.show()
4. まとめ
以上が、NumPy配列のサイン(正弦)の値を取得する関数です。それぞれ抑えておくと良いでしょう。なお、コサイン(余弦)の値を取得するには、cos関数を使います。

コメント