ベクトルの引き算の求め方と計算方法の初心者のための解説

ベクトルの引き算は、幾何学的には、反転したベクトルとの和で求めることができます。成分表示においては、単純にそれぞれの座標ごとに引き算をすることで求めることができます。

このベクトルの引き算を使いこなせるようにあると、例えば、速度 \( \vec{a} \) で移動する車の中から、速度 \( \vec{b} \) で飛んでいく鳥の速度はどのように見えるのかなどといった相対速度を求めることが簡単になります。

このページでは、このベクトルの引き算の求め方と、成分表示における計算方法をわかりやすく解説していきます。なお、ベクトルの最も基本的な知識については『ベクトルの意味とは：初学者がまず抑えておくべき基礎の基礎』で解説していますので、ぜひご確認ください。

1. ベクトルの引き算の求め方

以下のようにベクトル \( \vec{a} \) と \( \vec{b} \) があるとします。これらのベクトルの引き算はどうなるでしょうか。

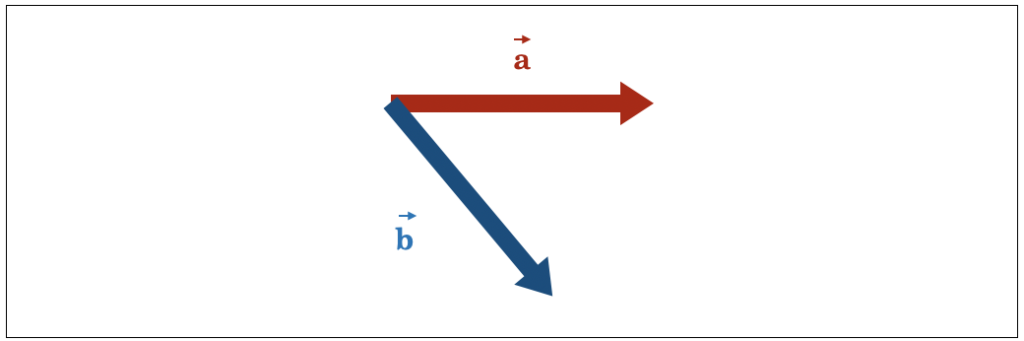
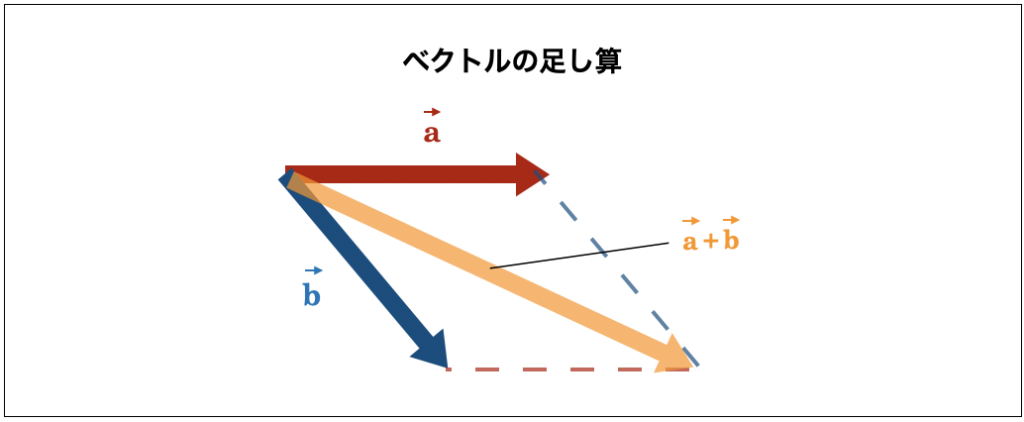
まず、ベクトルの和 \( \vec{a} + \vec{b} \) は、それぞれのベクトルが作る平行四辺形の対角線で求めるものでした。

一方で、ベクトルの引き算 \( \vec{a} – \vec{b} \) は、まず \( \vec{b} \) を正反対の方向に伸ばして \( -\vec{b} \) を作り、そして \( \vec{a} \) と \( -\vec{b} \) が作る平行四辺形の対角線を描くという2ステップで求められます。

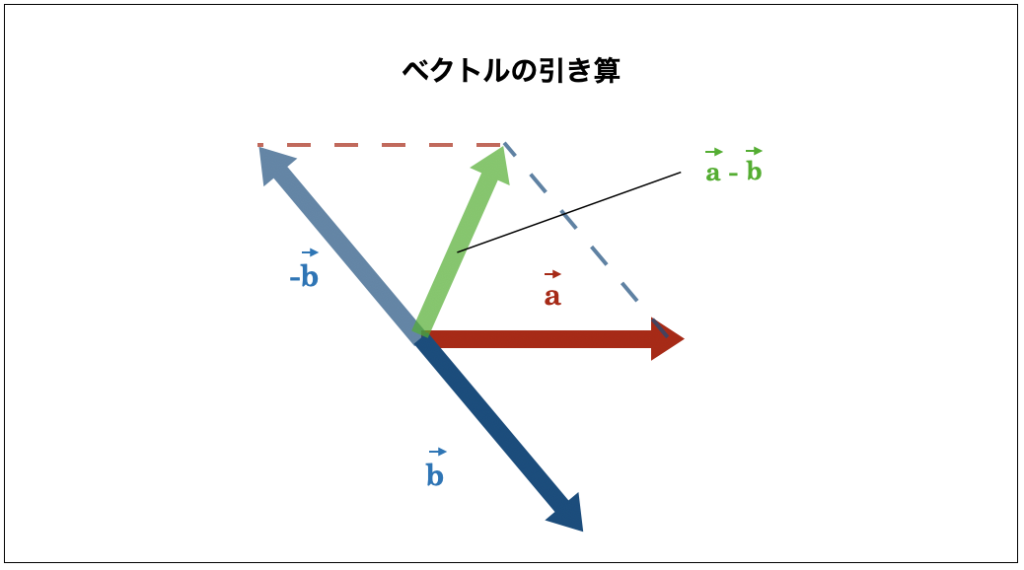
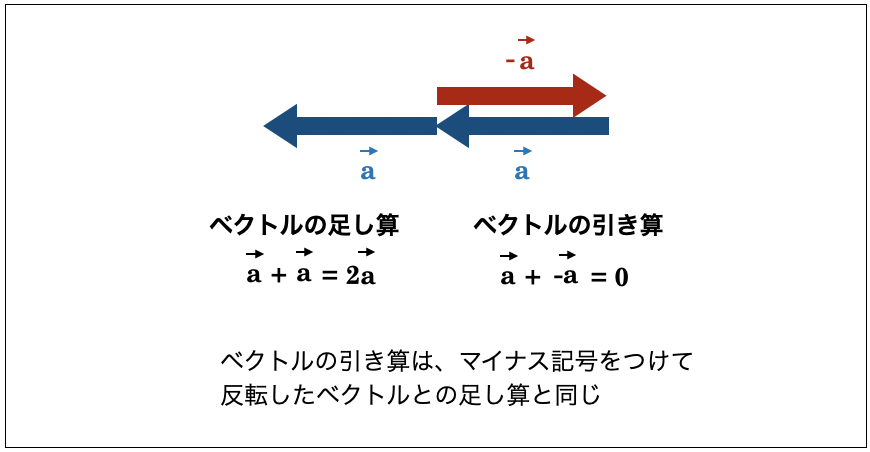
つまり、ベクトルの引き算 \( \vec{a} – \vec{b} \) は、\( \vec{a}\) と、 \( \vec{b}\) を反転した \(-\vec{b} \) との和を求めることと同じということです。

それでは、なぜ \( \vec{b} \) を反転すると \( -\vec{b} \) になるのでしょうか？

最も簡単な例を考えてみましょう。例えば、時速100kmで左に進む車の荷台の上から、反対向きに時速100kmで野球ボールを投げたとします。車の速度を \( \vec{a} \)、ボールの速度を \( \vec{b} \) とします。この時、静止した人から見て、このボールはどのように見えるでしょうか？

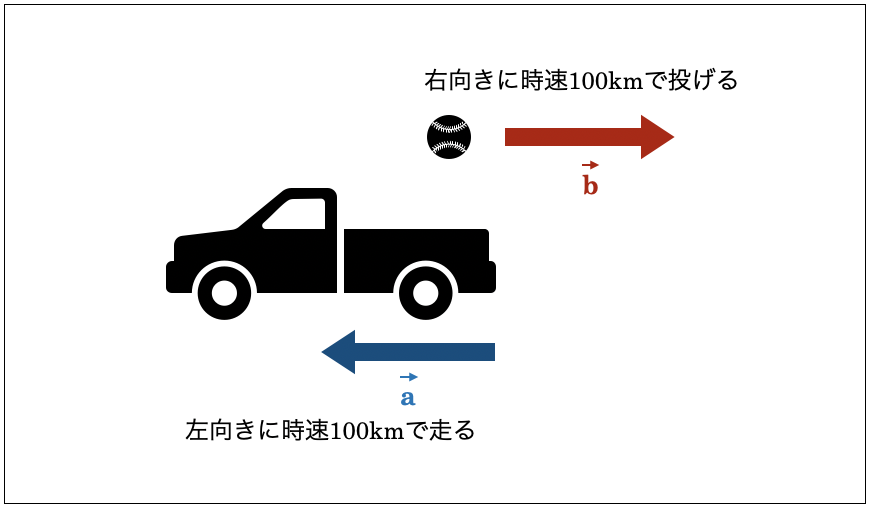
静止した人から見ると、投げた瞬間のボールの速度ベクトルは \( \vec{a}+\vec{b} \) になります。ベクトルの和は、ベクトルの矢印を継ぎ足すことで求められますから、それで考えると \( \vec{a}+\vec{b} \) は、以下のように出発点に戻ることになります。

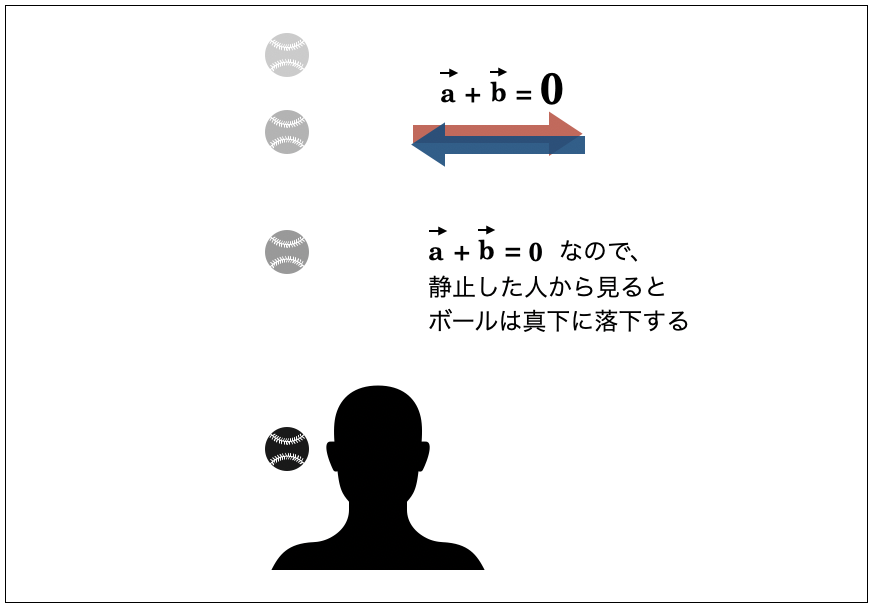
そのため、静止した人から見るとボールは横方向には動かず、重力で真下に落下することになります。

この時、\( \vec{a}+\vec{b}=0 \) です。そして、\( \vec{a}=100 \) であるため、\( \vec{b}=-100 \) ということになります。つまり、\( \vec{b}=-\vec{a} \) です。

ということは、\( \vec{a}+\vec{b}=\vec{a}-\vec{a}=0\) になります。

つまり、\( \vec{a} \) にとって \( -\vec{a} \) は向きを正反対にしたものとなるということです。だからこそ、ベクトルの引き算は、反転したベクトルとの和になるのです。

2. ベクトルの引き算でわかること

それでは、ベクトルの引き算でどのようなことがわかるのでしょうか。

簡単に言うと、移動中の物体から見た時の、ある物体の相対速度を求めることができます。

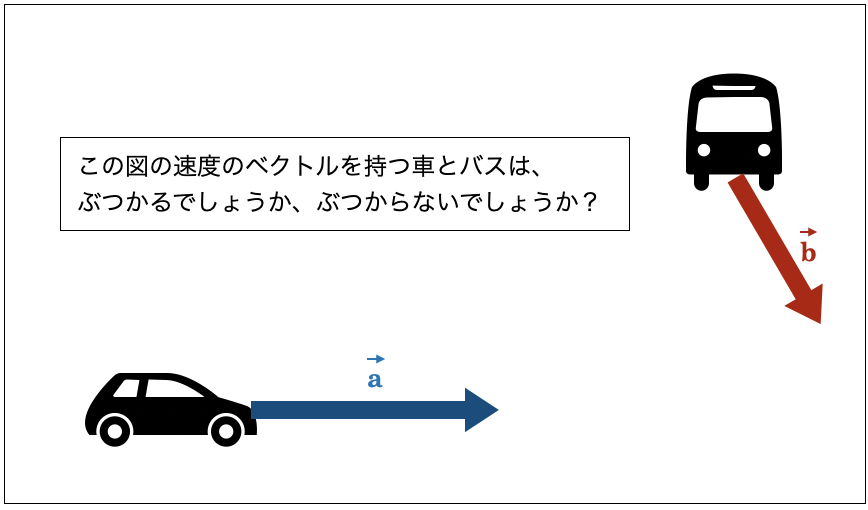
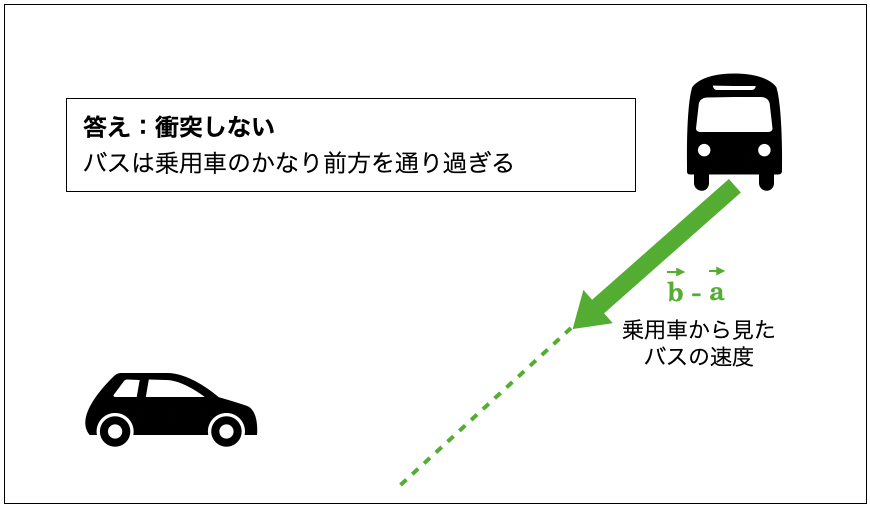
例として以下の画像をご覧ください。東向きに進む乗用車と南東向きに進むバスはぶつかるでしょうか、ぶつからないでしょうか？ベクトルの引き算を使うと、このような問題を簡単に解くことができます。

乗用車に乗っているところを想像してみましょう。乗用車の中の人から見ると、外の景色は、乗用車の速度 \( \vec{a} \) と同じ速さで逆向きに進むように見えるはずです。つまり、外の景色が \( -\vec{a} \) で動いていくように見えます。

バスは元々速度 \( \vec{b} \) で動いているので、乗用車から見て、バスが近づいてくる速度は、\( \vec{b}+(-\vec{a}) \)、つまり、\( \vec{b}-\vec{a} \) になります。

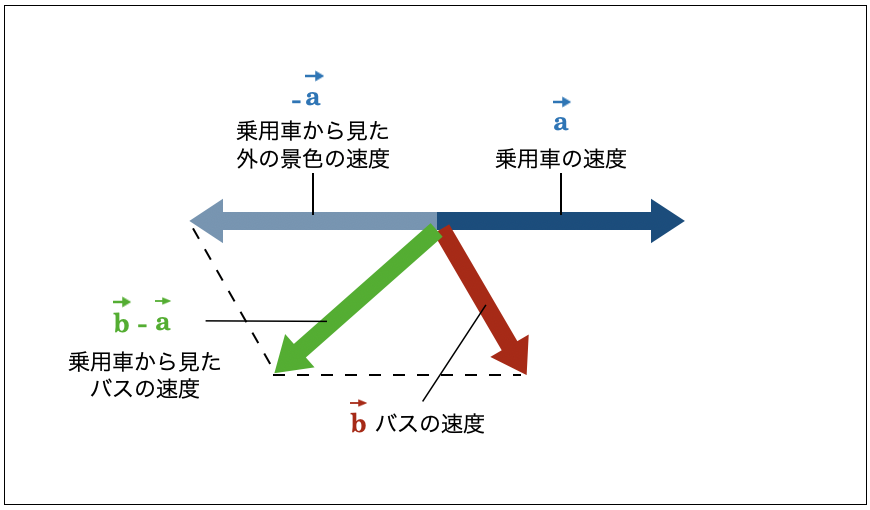
それでは、元の位置関係に戻って、この乗用車から見た時のバスが近づいてくる速度 \( \vec{b}-\vec{a} \) を当てはめてみましょう。すると、ご覧のようにバスは乗用車のかなり前方を通り過ぎることがわかります。

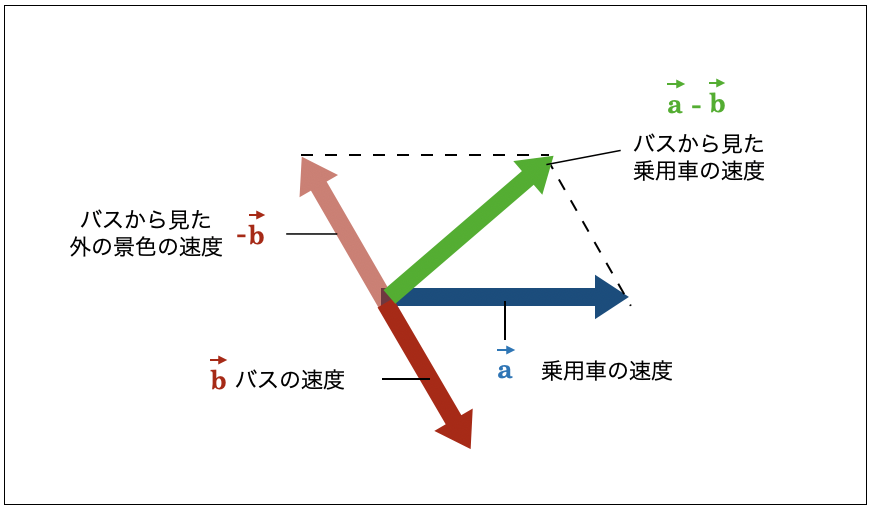
これと同じことをバスに乗っている人の目線に立った場合でも計算することが可能です。バスに乗っている人から見れば、外の景色は \( -\vec{b} \) で動いていくように見えます。そのため乗用車は、\( \vec{a}-\vec{b} \) の速度で近づいてくるように見えます。

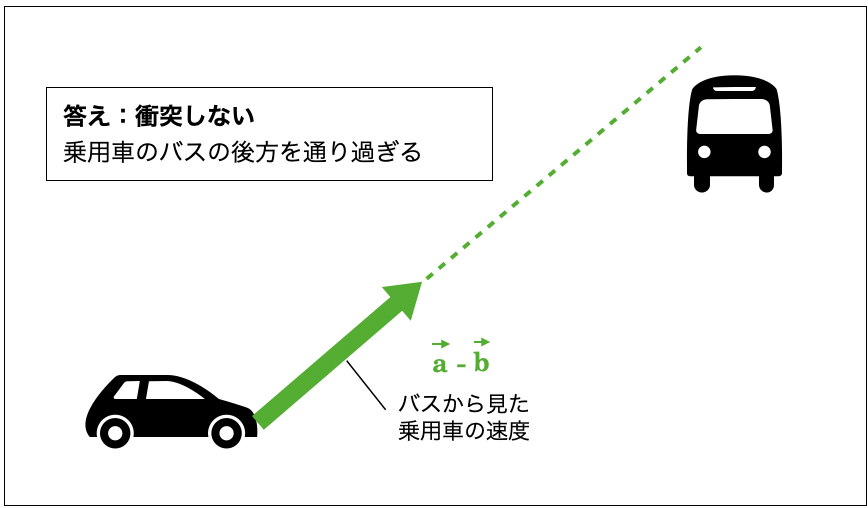
この \( \vec{a}-\vec{b} \) を元々の位置関係に当てはめてみると、やはりバスと乗用車はギリギリで衝突しないことが確認できます（ただし乗用車とバスの体積が大きい場合は衝突するかもしれません）。

このようにベクトルの引き算を使うと、相対速度の計算が簡単になるのです。

3. 成分表示でのベクトルの引き算

さて、ここまではベクトルを矢印で表して、幾何学的に(形状や図案によって)説明してきました。しかし「ベクトルとは」で解説しているように、ベクトルは数の組み合わせで表すこともできます。

平面の2次元ベクトルなら、\( \vec{a} = (3, 4) \) というように2つの数の組み合わせで、空間の3次元ベクトルなら \( \vec{a} = (3, 4, 5) \)というように3つの数の組み合わせで表現することができます。これを「ベクトルの成分表示」といいます。

そして、この成分表示を使うとベクトルの引き算がより簡単に行うことができます。そのため、ベクトルの計算においては、幾何学よりも成分表示を使うのが普通です。

それでは、以下のような \( x, y \) 座標の平面ベクトルを考えてみましょう。

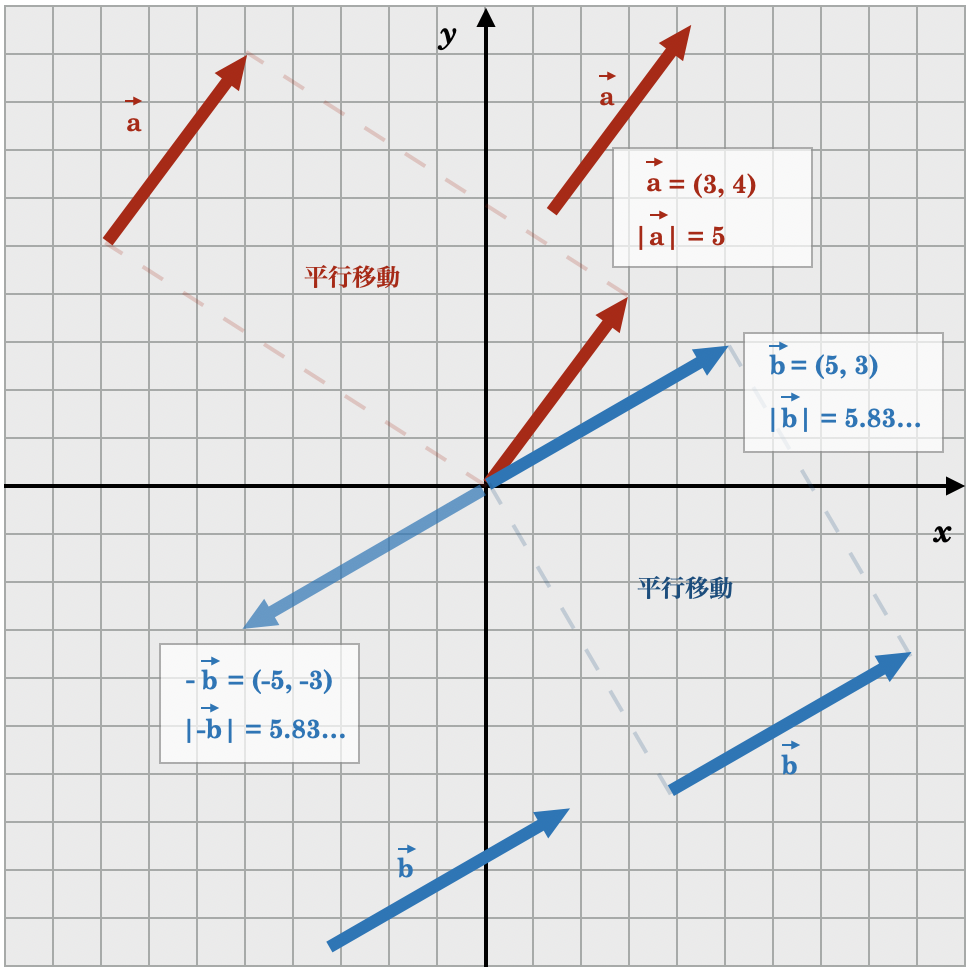
この図表には \( \vec{a} \) と \( \vec{b} \) の 二つのベクトルがあります。それぞれのベクトルを平行移動させて、その後端を原点に持ってくると、\( \vec{a} \) の\( x \)座標は\( 3 \)で\( y \)座標は\( 4 \)、\( \vec{b} \) の\( x \)座標は\( 5 \)で\( y \)座標は\( 3 \)であることがわかります。つまり、\( \vec{a} = (3, 4) \) 、 \( \vec{b} = (5, 3) \) と成分表示することが可能です。

そして、\( \vec{a} – \vec{b} \) を求めるとしたら、\( -\vec{b} \) は \( \vec{b} \) の正反対のベクトルですから \( -\vec{b} = (-5, -3) \) になります。

このようにベクトルの成分表示を使えば、三平方の定理 \(x^2 = y^2 + z^2 \) を用いて、それぞれのベクトルの長さ(速度における速さや、力における大きさ) \( |\vec{a}| \) と \( |-\vec{b}| \) も簡単に求められます。

\( |\vec{a}| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 \)
\(| -\vec{b}| = \sqrt{(-5^2)+(-3^2)} = \sqrt{25+9} = \sqrt{35} = 5.83… \)

さて、それでは \( \vec{a} – \vec{b} \) はどうなるでしょうか？

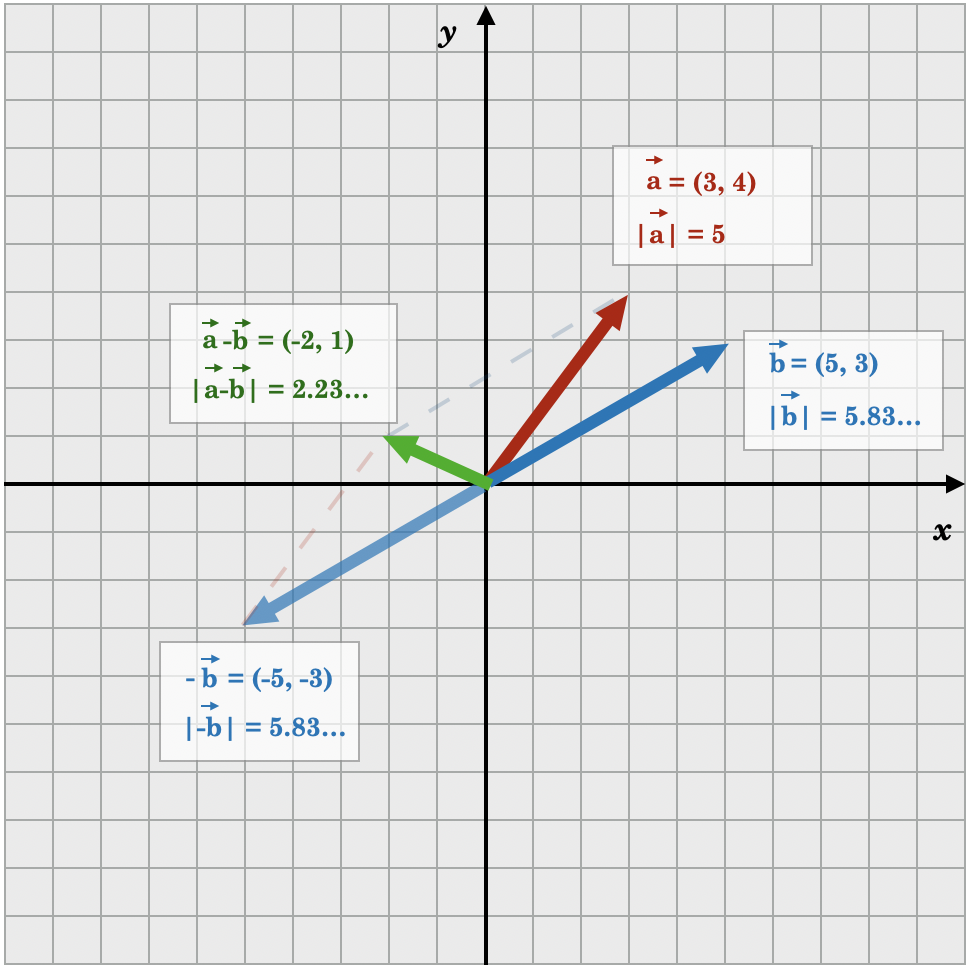
まず、\(\vec{a} – \vec{b} \) の座標を求めるには、\( \vec{a} \) と \(- \vec{b} \) の \( x \)座標同士と\( y \)座標同士を足し合わせます。つまり、\( \vec{a}+(-\vec{b}) = (3+(-5), 4+(-3))=(-2, 1) \) になります。

なお単純に、 \( \vec{a} \) と \( \vec{b} \) の、\( x \)座標同士と \( y \)座標同士を引き算すると覚えておいても構いません。つまり、\(\vec{a} – \vec{b} = (3-5, 4-3)=(-2, 1) \) になります。むしろ、成分表示における計算では、こちらの方が普通でしょう。

それでは、ベクトル \(\vec{a} – \vec{b} \) の長さはどうなるでしょうか。次の式で求めることができます。

\( |\vec{a}-\vec{b}| = \sqrt{(-2^2)+1^2} = \sqrt{4+1} = \sqrt{5} = 2.23… \)

まとめると、成分表示においては、ベクトルの引き算は、対象となるベクトルを座標ごとに引き算したものとなります。つまり、\( \vec{a} = (x_1, y_1) \)、\( \vec{b} = (x_2, y_2) \) としたら、ベクトルの引き算は、次の式で表すことができます。

\( \vec{a}-\vec{b} = (x_1-x_2, y_1-y_2)\)

そして、ベクトルの和の長さ(速さや大きさ)は、三平方の定理を使って、次の式で表すことができます。

\(|\vec{a}-\vec{b}| = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \)

これらの式を頭に入れておくと良いでしょう。

なお、この考え方は、3つ以上のベクトルの引き算でも、3次元ベクトル以上を扱う場合でも全く同じです。

4. まとめ

以上がベクトルの引き算です。あらためて重要ポイントをまとめておきましょう。

これらの点を頭に入れておくと良いでしょう。

なおPythonでは、これらを簡単に求めることができます。まず、ベクトルは、NumPyの配列で作成することができます。そして、ベクトル同士の引き算には -演算子を使います。

import numpy as np
# 2次元ベクトルの引き算
a = np.array([3, 5])
b = np.array([6, 2])
c = a-b
c

array([-3,  3])

このベクトルの大きさを求めたい時は、numpy.linalg.norm()関数を使います。

# ベクトルの大きさ
from numpy import linalg as LA
LA.norm(c)

4.242640687119285

3次元ベクトルや、それ以上のベクトルでも簡単に引き算したり、長さを求めるたりが可能です。

# 3次元ベクトルの引き算
a = np.array([3, 5, 2])
b = np.array([6, 2, 10])
c = a-b
c

array([-3,  3, -8])

# ベクトルの大きさ
from numpy import linalg as LA
LA.norm(c)

9.055385138137417