ベクトルの足し算(和)は、幾何学的には「二つのベクトルを継ぎ足したときの最終的な座標に対して、原点から伸びる新しいベクトル」です。数学的には「二つのベクトルの座標を成分ごとに足し合わせたもの」です。
これはベクトルの掛け算と並んで、「線形空間」と呼ばれる線形代数の土台を形成する重要な概念の一つです。
当ページでは、このベクトルの和について、アニメーションを使いながら、誰でも簡単に理解できるように解説していきます。
それでは始めましょう。
1. ベクトルの足し算(和)とは
まずは、ベクトルの足し算(和)を幾何学的にイメージできるように解説します。
ベクトルの足し算(和)とは、言葉で言うと「一方のベクトルの先端に、他方のベクトルのお尻を継ぎ足したときの最終的な行き先に対して、原点から伸びるベクトル」です。
視覚的な理解を得るために以下のアニメーションをご覧ください。
このようにベクトルの足し算(和)とは、「複数のベクトルを継ぎ足したときの最終的な行き先へ向かって、原点から伸びる新しいベクトル」です。
3次元ベクトルも同じです。以下のアニメーションを確認してください。
なお、この2つのアニメーションでは、\(\vec{v}+\vec{w}\) と \(\vec{w}+\vec{v}\) が同じであることも示しています。これはベクトルの重要な性質のうちの一つなので覚えておきましょう。
それでは確認のため、2次元空間と3次元空間におけるベクトルの和の画像をあらためて載せておきます。
以下は2次元空間におけるベクトルの和です。
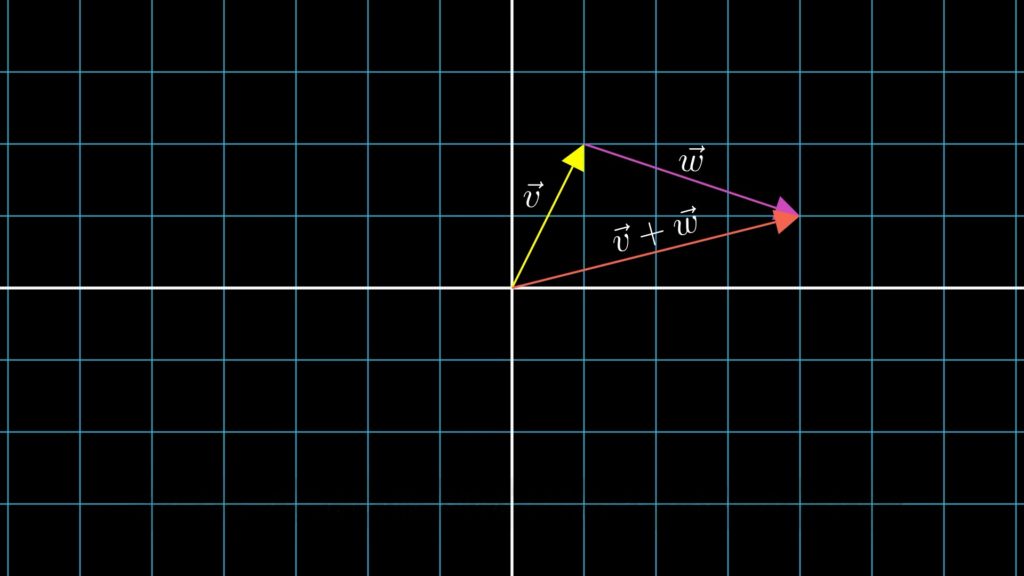
そして以下は、3次元空間におけるベクトルの和です。
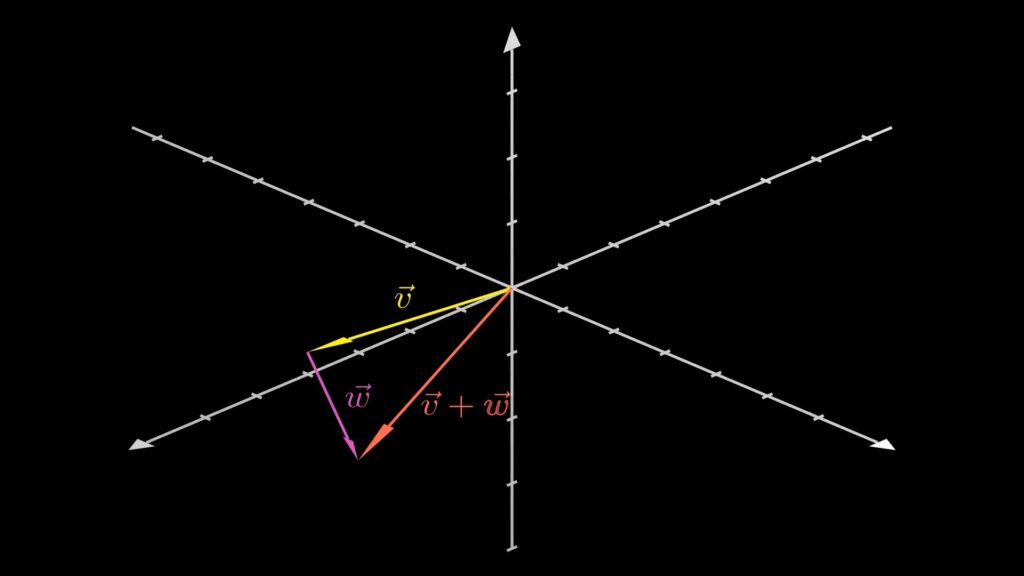
2. ベクトルの足し算(和)の計算方法
それでは次に、ベクトルの足し算(和)の計算方法を確認しておきましょう。ベクトルの和は次のように、それぞれの成分ごとの足し算で求めます。
2次元ベクトルの和
\[\begin{eqnarray}
\vec{v}+\vec{w}=
\left[ \begin{array}{c} v_1 \\ v_2 \end{array} \right]
+
\left[ \begin{array}{c} w_1 \\ w_2 \end{array} \right]
=
\left[ \begin{array}{c} v_1+w_1 \\ v_2+w_2 \end{array} \right]
\end{eqnarray}\]
3次元ベクトルの和
\[
\vec{v}+\vec{w}=
\left[ \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right]
+
\left[ \begin{array}{c} w_1 \\ w_2 \\w_3 \end{array} \right]
=
\left[ \begin{array}{c} v_1+w_1 \\ v_2+w_2 \\ v_3+w_3 \end{array} \right]
\]
なぜ、この計算でベクトルの和が求められるのかは、以下のアニメーションをご覧頂くと、視覚的にハッキリと理解することができます。
参考のために、2次元ベクトルの和と3次元ベクトルの和の計算例を一つずつ載せておきます。
まずは2次元ベクトルの和です。
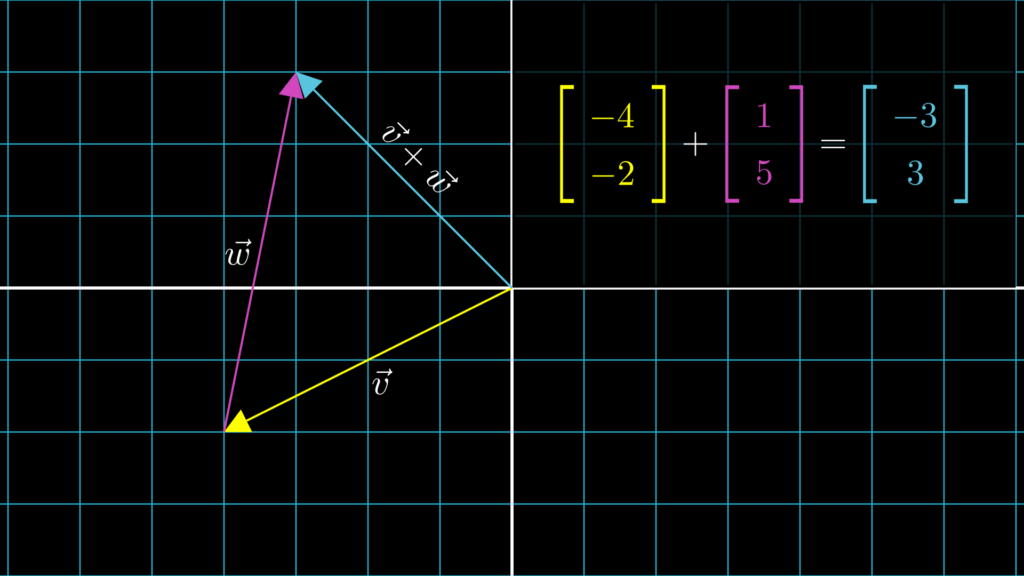
次に3次元ベクトルの和です。
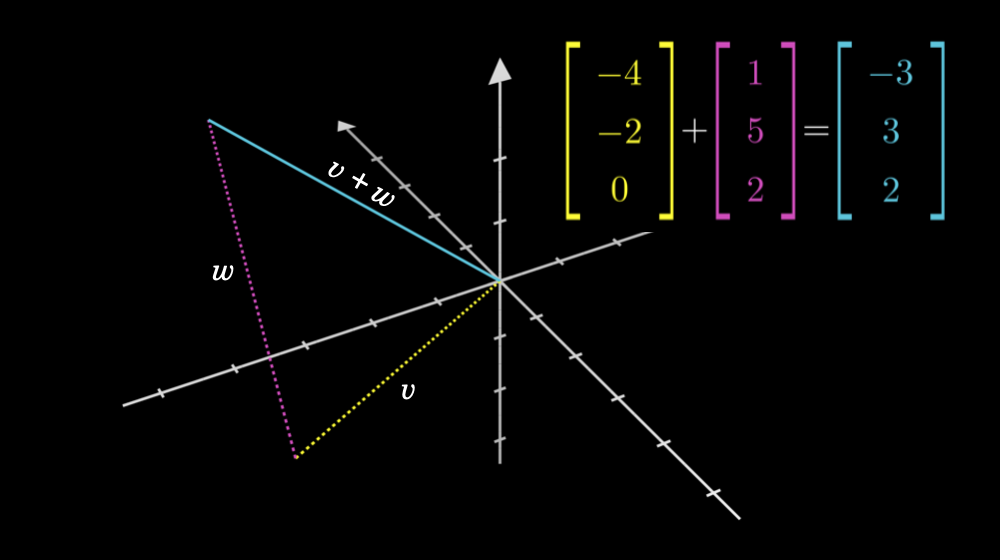
3. ベクトルの和の性質
さて、ベクトルの和には重要な4つの性質があります。それが以下のものです。
- \(\vec{v}+\vec{w}=\vec{w}+\vec{v}\)
- \((\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})\)
- \(\vec{v}+\vec{0}=\vec{v}\)
- \(\vec{v}+(-\vec{v})=\vec{0}\)
この4つの性質と、ベクトルの掛け算の4つの性質を合わせた8つはベクトルの公理(ベクトルについて話し合うための共通の前提)であり、線形代数について考えるための土台となる重要なものです。
これらの性質の一つ一つを理解することは、決して難しくありません。アニメーションで視覚的に確認すると簡単に理解することができます。それぞれ見ていきましょう。
\(\vec{v}+\vec{w}=\vec{w}+\vec{v}\)
上でも触れましたが、ベクトルの和は足す順番が逆になっても結果は同じです。以下のアニメーションであらためてご確認ください。
計算例
\[\begin{eqnarray}
\vec{v}+\vec{w}
&=&
\left[ \begin{array}{c} -2 \\ 3 \end{array} \right]
+
\left[ \begin{array}{c} 6.5 \\ -2 \end{array} \right]
=
\left[ \begin{array}{c} 4.5 \\ 1 \end{array} \right] \\
&\upharpoonleft\downharpoonright& \\
\vec{w}+\vec{v}
&=&
\left[ \begin{array}{c} 6.5 \\ -2 \end{array} \right]
+
\left[ \begin{array}{c} -2 \\ 3 \end{array} \right]
=
\left[ \begin{array}{c} 4.5 \\ 1 \end{array} \right] \\
\end{eqnarray}\]
\((\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})\)
3つ以上のベクトルの足し算でも同じです。どのような順番で足しても最終的に得られるベクトルは変わりません。
計算例
\[\begin{eqnarray}
(\vec{u}+\vec{v})+\vec{w}
&=&
\left(
\left[ \begin{array}{c} -4 \\ 0 \end{array} \right]
+
\left[ \begin{array}{c} -1 \\ 2 \end{array} \right]
\right)
+
\left[ \begin{array}{c} 6.5 \\ -3.5 \end{array} \right]
=
\left[ \begin{array}{c} -5 \\ 2 \end{array} \right]
+
\left[ \begin{array}{c} 6.5 \\ -3.5 \end{array} \right]
=
\left[ \begin{array}{c} 1.5 \\ -1.5 \end{array} \right]\\
&\upharpoonleft\downharpoonright& \\
\vec{u}+(\vec{v}+\vec{w})
&=&
\left[ \begin{array}{c} -4 \\ 0 \end{array} \right]
+
\left(
\left[ \begin{array}{c} -1 \\ 2 \end{array} \right]
+
\left[ \begin{array}{c} 6.5 \\ -3.5 \end{array} \right]
\right)
=
\left[ \begin{array}{c} -4 \\ 0 \end{array} \right]
+
\left[ \begin{array}{c} 5.5 \\ -1.5 \end{array} \right]
=
\left[ \begin{array}{c} 1.5 \\ -1.5 \end{array} \right]
\end{eqnarray}\]
\(\vec{v}+\vec{0}=\vec{v}\)
これはアニメーションにする必要がないので割愛します。あるベクトルにゼロベクトルを足しても何も変わりません。
計算例
\[\begin{eqnarray}
\vec{v}+\vec{0}
&=&
\left[ \begin{array}{c} -2 \\ 3 \end{array} \right]
+
\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
=
\left[ \begin{array}{c} -2 \\ 3 \end{array} \right]
\end{eqnarray}\]
\(\vec{v}+(-\vec{v})=\vec{0}\)
ベクトル \(\vec{v}\)と、そのベクトルを \(-1\) 倍したものを足すとゼロベクトルになります。なお、ベクトルの掛け算については『ベクトルの掛け算とは何か?幾何学的な意味と計算方法の解説』で解説します。
計算例
\[\begin{eqnarray}
\vec{v}+(-\vec{v})
&=&
\left[ \begin{array}{c} -2 \\ 3 \end{array} \right]
+
\left[ \begin{array}{c} 2 \\-3 \end{array} \right]
=
\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
\end{eqnarray}\]
以上がベクトルの和の4つの性質です。
4. 練習問題
最後に練習問題を用意しておきますので、理解を深めるために、ぜひ一度ご自身で解いてみてください。以下のボックスをクリックすると、問題と解答を確認することができます。
5. まとめ
以上がベクトルの和です。
こうして見てみるととても単純なものですが、冒頭で述べたとおり、これは線形代数において、ベクトルの積と並んで核となる計算です。
この記事が理解を深める助けとなったなら嬉しく思います。
次に読みたいページ
ベクトルの和について理解したら、次はベクトルの掛け算をマスターしましょう。『ベクトルの掛け算とは何か?幾何学的な意味と計算方法の解説』で解説していますので、ぜひご覧ください。








コメント
コメント一覧 (1件)
とても分かりやすいです!感動しました!