微分積分学において、三角関数は、べき乗関数・指数関数・対数関数と並んで、理解しておくべき4つの関数の一つです。
試験問題では、何やら複雑な関数をたくさん見せられるので、「たった4つだけ?」と思われるかもしれません。実は、試験問題に出てくるような関数は、現実世界とは全く関係のないデタラメなものばかりです。それは、単なる数学クイズであって、現実世界の問題解決に活かせるようなものではありません。
一方で、三角関数は、パッと思いつくだけでも、景気循環・日照時間の変動・振り子運動・交流電源電圧・躁うつ病などなど、ここに収まらないほど数多くの現実世界の事象を表しており、さまざまな分野の発展に大きく貢献しているのです。
だからこそ、三角関数の積分を深く理解することは、とても重要です。そこで、ここでは三角関数の積分の公式と、三角関数を現実世界の問題解決に活用する際に知っておきたい3つの性質について、わかりやすく解説していきます。
1. 三角関数の積分公式
三角関数の積分の公式は以下の通りです。
三角関数の積分
\[\begin{eqnarray}
\int \sin x dx
&=&
-\cos x + C\\
\int \cos x dx
&=&
\sin x + C\\
\int \tan x dx
&=&
-log|\cos x| + C\\
\end{eqnarray}\]
結局のところ、現実世界の問題解決においてよく使われるのは \(\sin\) と \(\cos\) です。そのため、この二つはとても重要です。一方で \(\tan\) の積分を使う機会は非常に限られています。
そのため、まずは \(\sin\) と \(\cos\) の積分をしっかりと理解しておきましょう。そうしておけば結果的に \(\tan\) の積分も理解しやすくなります。
なお、「それぞれの積分が、なぜ公式のようになるのか?」については、それぞれ以下のページで解説しています。これらのページをご覧いただくと、「なぜ積分は微分の反対の演算なのか?」という点を深く理解するための助けにもなりますので、ぜひご覧ください。
2. 三角関数の微分積分の3つの性質
さて、三角関数の積分(厳密には \(\sin\) と \(\cos\) の積分)には、次の3つの性質があります。
- 反転性
- 循環性
- スライド性
これらは受験勉強では学ぶことはあまりないと思いますが、微分積分を現実世界の問題解決に応用する上では、とても重要な知識ですので、しっかりと抑えておくと良いでしょう。
2.1. 反転性
三角関数(\(\sin\) と \(\cos\))の積分の一つ目の性質は、微分と比べて、正負が反転するという点です。具体的には「\(\sin(x)\) の積分は \(-\cos(x)\)、微分は \(\cos(x)\) 」になります。そして「\(\cos(x)\) の積分は \(\sin(x)\)、微分は \(-\sin(x)\)」になります。
\(\sin\) の微積分の反転性
\[\begin{eqnarray}
\cos(x)
\hspace{5mm}
\xleftarrow{微分}
\hspace{5mm}
&\sin(x)&
\hspace{5mm}
\xrightarrow{積分}
\hspace{5mm}
-\cos(x)\\
\end{eqnarray}\]
\(\cos\) の微積分の反転性
\[\begin{eqnarray}
-\sin(x)
\hspace{5mm}
\xleftarrow{微分}
\hspace{5mm}
\cos(x)
\hspace{5mm}
\xrightarrow{積分}
\hspace{5mm}
\sin(x)
\end{eqnarray}\]
それぞれ視覚的にも確認しておきましょう。まずは \(\sin(x)\) の微分と積分です。
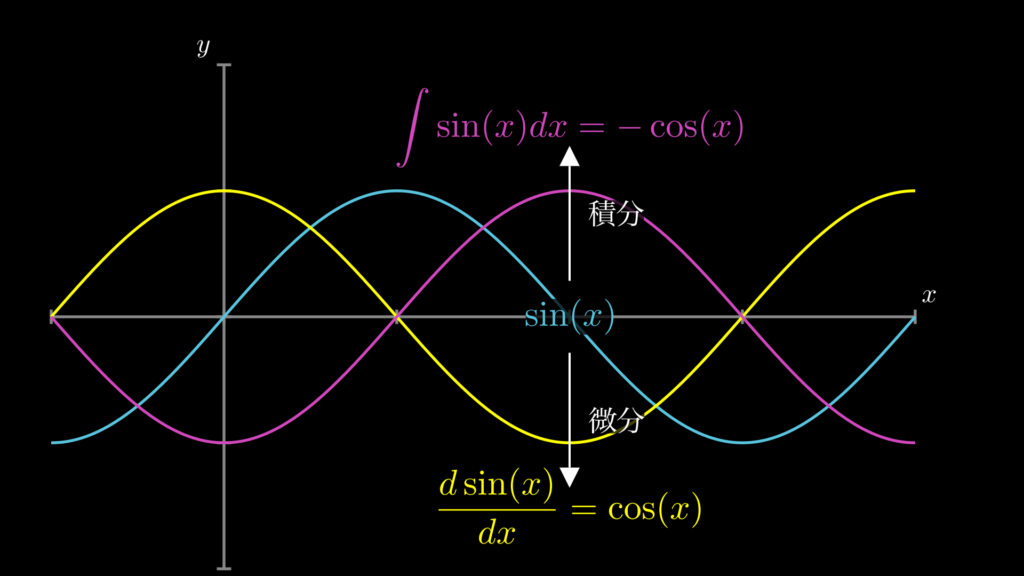
次に \(\cos(x)\) の微分と積分です。
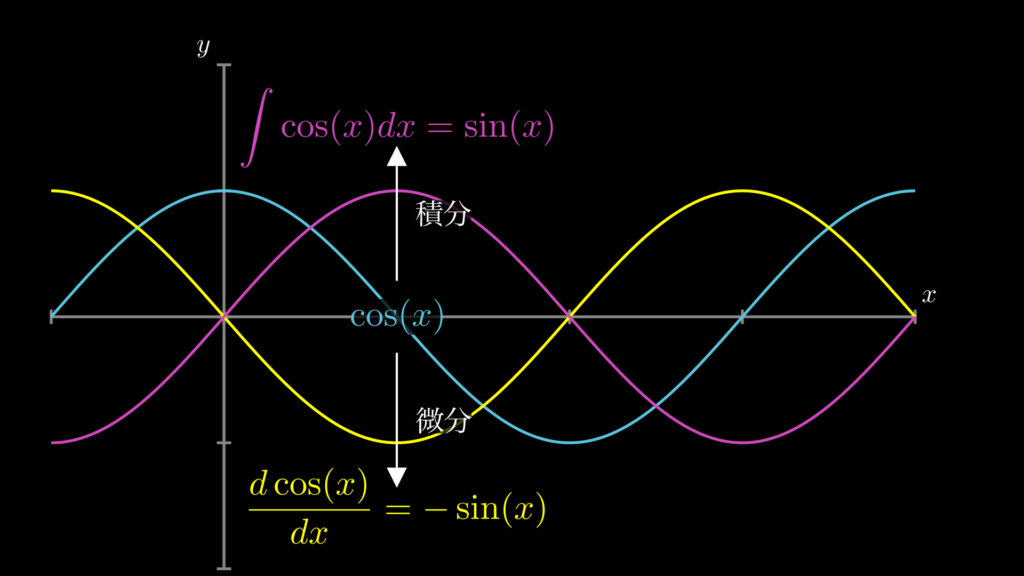
このように \(\sin\) と \(\cos\) は、微分と積分で正負が反転するという性質があります。
2.2. 循環性
三角関数(\(\sin\) と \(\cos\))の積分の二つ目の性質は、積分(または微分)を4回すると、元に戻るという点です。以下でご確認ください。
三角関数の微積分の循環性
(時計回りが積分・反時計回りが微分)
\[
\begin{array}{ccc}
\sin(x) & \rightarrow & -\cos(x) \\
\uparrow & & \downarrow \\
\cos(x) & \leftarrow & -\sin(x)
\end{array}
\]
以下のようにアニメーションで確認しておくと、より理解しやすくなりますので、ぜひご覧ください。\(\sin(x)\) から4回積分すると、元の \(\sin(x)\) に戻る様子を示しています。
以上が三角関数の微積分の循環性です。
2.3. スライド性
三角関数(\(\sin\) と \(\cos\))の積分の三つ目の性質は、積分をすると \(\frac{\pi}{2}\) だけ左にずれるという点です。逆に言うと、微分をすると \(\frac{\pi}{2}\) だけ右にずれます。
\(\sin\) の微積分のスライド性
\[\begin{eqnarray}
\sin(x+\frac{\pi}{2})=\cos(x)
\hspace{5mm}
\xleftarrow{微分}
\hspace{5mm}
&\sin(x)&
\hspace{5mm}
\xrightarrow{積分}
\hspace{5mm}
\sin(x-\frac{\pi}{2})=-\cos(x)\\
\end{eqnarray}\]
\(\cos\) の微積分のスライド性
\[\begin{eqnarray}
\cos(x+\frac{\pi}{2})=-\sin(x)
\hspace{5mm}
\xleftarrow{微分}
\hspace{5mm}
\cos(x)
\hspace{5mm}
\xrightarrow{積分}
\hspace{5mm}
\cos(x-\frac{\pi}{2})=\sin(x)
\end{eqnarray}\]
それぞれ視覚的に確認しておきましょう。
まずは \(\sin(x)\) の積分です。微分をすると左にスライドし、積分をすると右にスライドすることが確認できます。
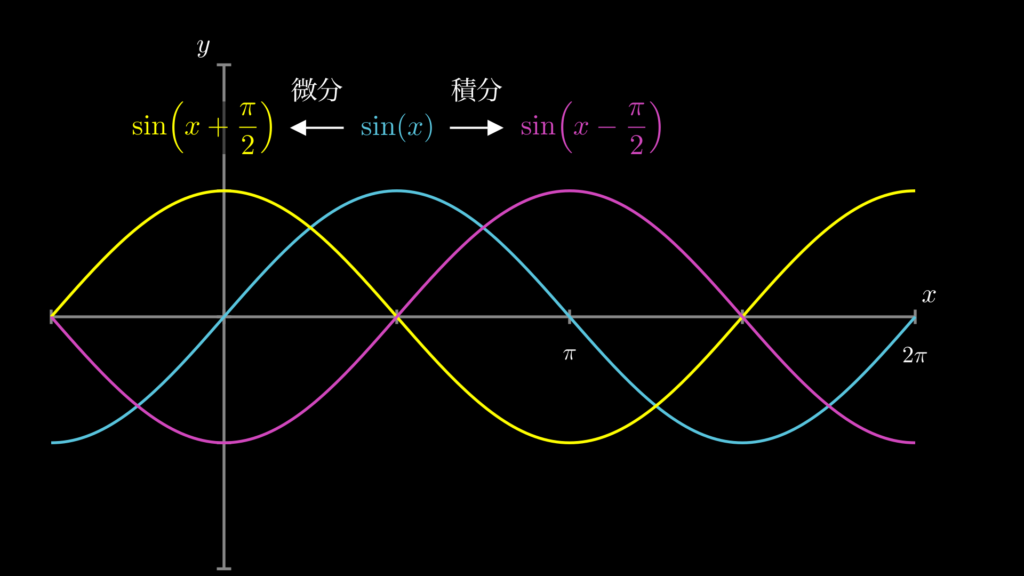
次に \(\cos(x)\) の積分です。上と同じように、微分をすると左にスライドし、積分をすると右にスライドすることが確認できます。
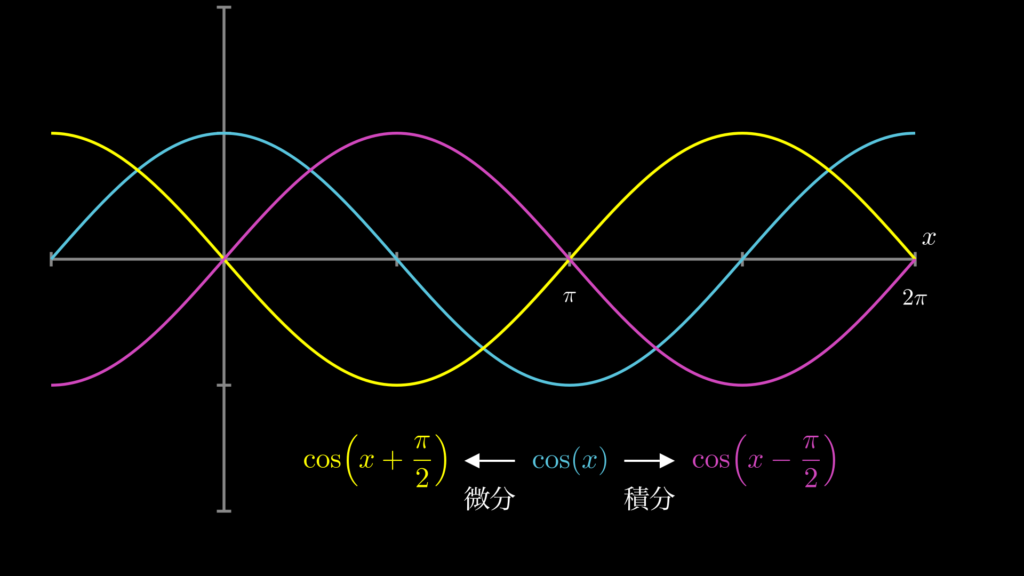
以上が三角関数の微積分のスライド性です。
3. 三角関数の積分まとめ
以上が三角関数の積分の公式と性質です。
特に、現実世界の問題に微分積分学を応用するには、お伝えした3つの性質を知っておくことがとても有用です。この3つの性質を一言で表すなら、「三角関数には、微分にせよ、積分にせよ、何回か繰り返すと元に戻る」ということです。
実は、このような性質を持つ関数は、三角関数以外にも指数関数があります。そして、三角関数の微積分と、指数関数の微積分を理解すると、複素数というものが理解できるようになっていきます。蛇足になるので、これ以上は、ここでは控えることにします。
当ページでは、三角関数のそれぞれの積分公式と、解説した3つの性質をしっかりと抑えておきましょう。




コメント