ガンマ分布は、「任意の単位時間や単位面積 λ の間に 1 回起きることが期待できる出来事が、実際に起きるまでの時間の分布」です。主に信頼性工学や通信工学において使われますが、以下のような実用例があります。
- 体重の分布
- エイズの潜伏期間
- システム・ダウンまでの待ち時間
- 電子部品の寿命
- 保険金の支払額のモデル
当ページでは、このガンマ分布についてわかりやすく解説していきます。具体的には以下のことを学ぶことができます。
当ページでわかること
- ガンマ分布が何でどういう時に使える確率分布なのかがわかる
- ガンマ分布の確率密度関数と分析指標の計算方法がわかる
- ガンマ分布のグラフの形状と性質がわかる
- ガンマ分布の具体例が例題を通してわかる
- ガンマ分布がどのように導出されたのかがわかる
なお確率分布とは何かについては『確率分布とは?誰でも必ず理解できるようにわかりやすく解説』で解説しているので、併せてご確認いただくと良いかと思います。
それでは始めましょう。
1. ガンマ分布とは
冒頭でもお伝えした通り、ガンマ分布とは「一定期間 λ の間に 1 回起きることが期待できる出来事が実際に起きるまでの時間の分布」です。
たとえば製品寿命が 10 年の (\(\lambda=10\))電子部品があるとします。この電子部品が実際に壊れるまでの期間は、以下のガンマ分布に従います。
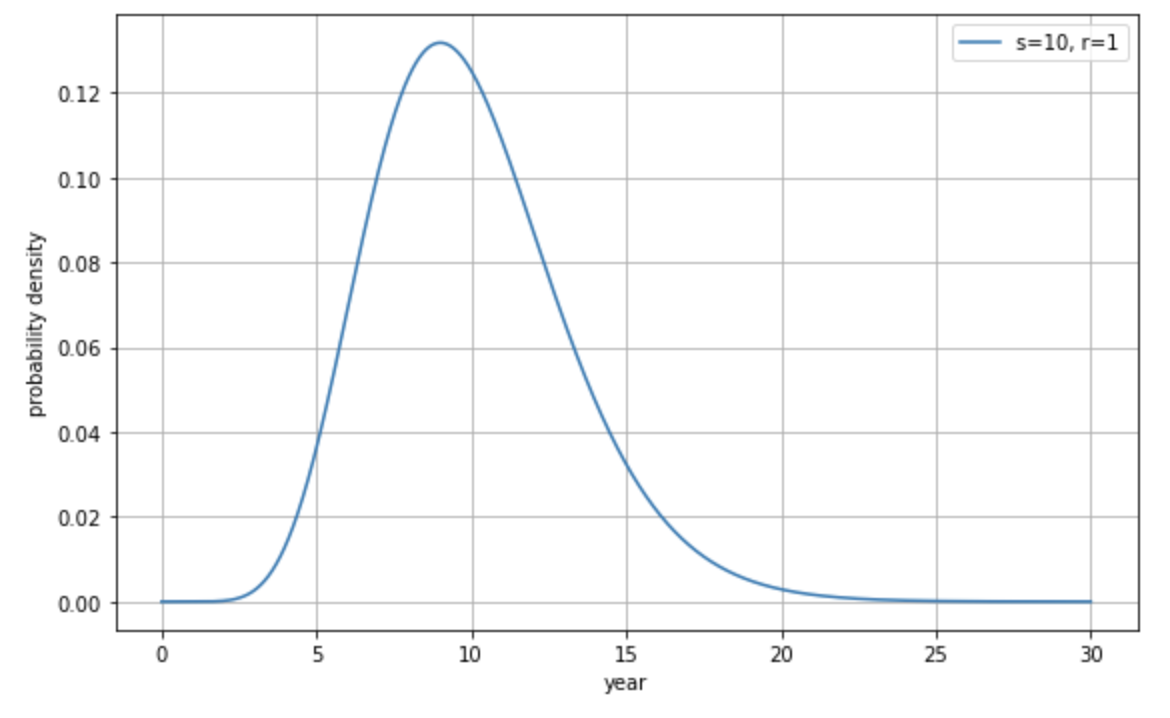
こうやって見てみると寿命が 10 年と言っても、5 年で壊れる場合もあれば、20 年経っても壊れない場合もあるということがわかります。
このように稀にしか起こらない出来事が実際に起こるまでの期間の分布を示すのがガンマ分布です。
2. ガンマ分布の確率密度関数
ガンマ分布の確率密度関数は次の通りです。
ガンマ分布の確率密度関数
\[\begin{eqnarray}
f(\lambda)
=
\dfrac{r^s}{\Gamma(s)}\lambda^{s-1}e^{-r\lambda}
\ \ \ \rm{for} \lambda > 0
\end{eqnarray}\]
\(\lambda\) : 確率変数, \(s\):形状母数, \(r\):尺度母数
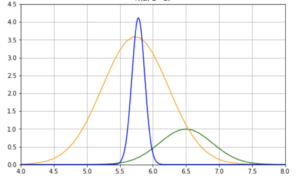
ご覧の通り、ガンマ分布は形状母数 \(s\) と尺度母数 \(r\) という 2 つのパラメータに依存しています。それぞれ異なる値を入れて見比べられるようにしたものが下図 1.1 です。
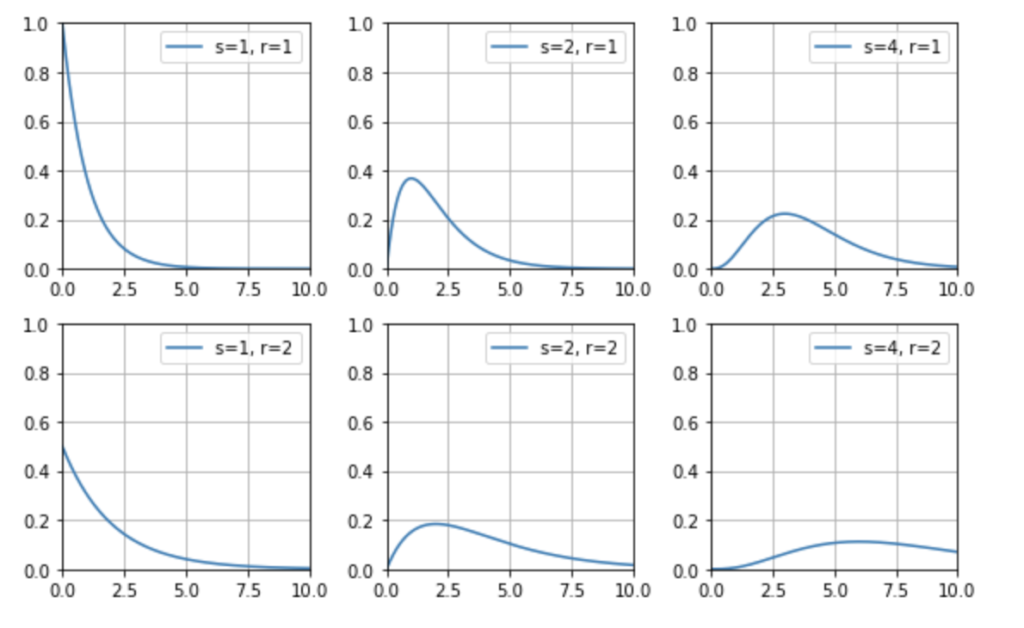
これらを眺めていると、ガンマ分布には決まった性質があることがわかります。
- 全体の共通点として、ガンマ分布 \(\lambda \sim \rm{Gamma}(s,r)\) の変数は常に正の整数であり、右斜めになっている。
- そして形状と右斜めへの減少の程度は、形状母数 \(s\) と尺度母数 \(r\) の 2 つのパラメータによってコントロールされる。
なお、ガンマ分布は次のように表される場合も多いです。
\[\begin{eqnarray}
f(\lambda)
=
\dfrac{1}{\Gamma(s)\theta^s}\lambda^{s-1}e^{-\dfrac{r}{\theta}}
\ \ \ \rm{for} \lambda > 0
\end{eqnarray}\]
違いは、ランダムな出来事が 1 回起こるまでの期間を \(1/\lambda\) という逆数で表す点にあります。これはガンマ分布をややこしいものにしてしまっている要因の一つですが、どちらを使うか統一されていないので、両方理解しておく必要があります。
3. ガンマ分布の期待値・最頻値・分散
ガンマ分布の代表的な分析指標は以下の公式で求められます。
- 期待値(平均値):\(E(\lambda)=\dfrac{s}{r}\)
- 最頻値(中央値):\(\rm{Mode}(\lambda)=\dfrac{s-1}{r} \ \ \ \rm{for} s \geq 1\)
- 分散:\(\rm{Var}(\lambda)=\dfrac{s}{r^2}\)
これらの定量的分析指標も、ガンマ分布について、いくつかの重要な気づきを与えてくれます。
まずガンマ分布の期待値は、\(s > r\) のときに 1 より大きくなり、 \(s < r\) のときに 1 より小さくなります。さらに、形状母数 \(s\) が、尺度母数 \(r\) と比べて相対的に大きくなるほど、\(\lambda\) の右斜めの程度が減少し、分散(グラフの広がり具合)が上昇します。
以下に簡単なクイズを用意しておいたので、ぜひ理解を深めるために、ご活用ください。
クイズ
1. “形状母数 \(s >\) 尺度母数 \(r\)” のとき \(\rm{Gamma}(s,r)\) の確率変数 \(\lambda\) の典型的な形状は、以下のうちどれでしょうか。
- a. 右斜め方向で期待値は 1 より大きい
- b. 右斜め方向で期待値は 1 より小さい
- c. 左右対称で期待値は 1
2. 上と同じ選択肢で、“形状母数 \(s <\) 尺度母数 \(r\)” のとき \(\rm{Gamma}(s,r)\)の確率変数 \(\lambda\) の典型的な形状はどうなるでしょうか。
3. \(\rm{Gamma}(20,20)\) と \(\rm{Gamma}(20,100)\) では、尤もらしい \(\lambda\) の値について、どちらの方がより分散が大きいでしょうか。
4. ガンマ分布の例
それでは例題を見て、ガンマ分布をどのように活用するのかを理解しましょう。
問題:電子部品の故障率は?
ある電子部品は 10 年に 1 度の割合で故障します。この電子部品について以下の問いに答えなさい。
- (1) 1 年以内に故障する確率
- (2) 5 年以内に故障する確率
- (3) 1 回故障するまでの年数(期待値)
まず 10 年に一度の割合で故障するということは、\(\rm{Gamma}(s,r)\) の形状母数 \(s=10\) 、尺度母数 \(r=1\) ということになります。そこで、これをグラフに描くと以下のようになります。

横軸が年数で縦軸が確率密度です。このグラフを見れば問題の答えが一目でわかります。
(1) 1 年以内に故障する確率:横軸の 1 年目のあたりを見てみると、これはゼロに近いことがわかります(ただしゼロとイコールではありません)。
(2) 5 年以内に故障する確率:これは横軸の 5 年目のところまでの曲線下の面積とイコールになります。厳密に計算するには面倒な積分が必要ですが、グラフを見ると、これはざっくりと 5 ~ 6 % ぐらいだろうと予測できます。
(3) 1 回故障するまでの期待値:これはグラフは必要ありません。ガンマ分布の期待値の公式より \(s\div r = 10\) 年ということがわかります。
5. ガンマ分布の導出(指数分布との関係)
実はガンマ分布は指数分布から導き出されています。具体的には、ガンマ分布は離散確率分布である幾何分布の、連続確率分布バージョンである指数分布を、一般化したものです。
まず幾何分布とは、「結果が成功か失敗の 2 つのみであり、成功率 \(p\) と失敗率 \(q\) がわかっている場合の、初めて成功するまでの試行回数の分布」です。これの確率質量関数は次の通りです。
\[\begin{eqnarray}
f(x)=pq^{x-1}, \ \ \ x = 1,2,3, \cdots
\end{eqnarray}\]
次に指数分布は、幾何分布を連続値にしたもので、「期間 \(1/\lambda\) に 1 回起きることが期待される事象が 1 回起きるまでの時間の分布」です。以下の確率密度関数で定義されます。
\[\begin{eqnarray}
f(x)=\lambda e^{-\lambda x}
\end{eqnarray}\]
さて、ガンマ分布は、この指数分布を一般化したものであり、「期間 \(1/\lambda\) に 1 回起こることが期待されるランダムな事象が \(k\) 回起こるまでの時間の分布」です。確率密度関数はあらためて次の通りです。
\[
f(x)
=
\dfrac
{\lambda^k}
{\Gamma(k)}
x^{k-1}
e^{-\lambda x}
\]
こうやって見比べてみると指数分布と似ていることがわかりますし、\(k=1\) にすると指数分布になることがわかります。なお、分母の \(\Gamma(k)\) は面積の総和を 1 にするための正規化定数です。
まとめ
最後に簡潔に内容をまとめておきます。
ガンマ分布とは
ガンマ分布は「一定期間 λ の間に 1 回起きることが期待できる出来事が複数回起きるまでの時間の分布」です。以下の公式によって定義されます。
\[\begin{eqnarray}
f(\lambda)
=
\dfrac{r^s}{\Gamma(s)}\lambda^{s-1}e^{-r\lambda}
\ \ \ \rm{for} \lambda > 0
\end{eqnarray}\]
\(\lambda\) : 確率変数, \(s\):形状母数, \(r\):尺度母数
ガンマ分布の分析指標
分析指標の公式は以下の通りです。
- 期待値(平均値):\(E(\lambda)=\dfrac{s}{r}\)
- 最頻値(中央値):\(\rm{Mode}(\lambda)=\dfrac{s-1}{r} \ \ \ \rm{for} s \geq 1\)
- 分散:\(\rm{Var}(\lambda)=\dfrac{s}{r^2}\)
以上、最後までご覧頂きありがとうございました。
当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります(コメント返信は余裕ができれば行いたいと考えています)。

コメント
コメント一覧 (3件)
教えてください。
ガンマ分布は「一定期間 λ の間に 1 回起きることが期待できる出来事が複数回起きるまでの時間の分布」とのことですが、
平均寿命が10年の製品が1年以内に故障する確率というのは、「10年に1回起きることが期待できる出来事(故障)が1回起きるまでの時間」における累積確率ではないのでしょうか?だとすれば指数分布だと思ったのですが、、、
故障の確率については指数関数でも応用例として取り上げている解説などもあり、混乱しています。よろしくお願いします。
形状母数 と尺度母数がなんなのかわかりません・・・
もっとわかりやすく教えていただければ助かります・・・
拝読し大変勉強になりました。誠に有り難うございます。
本文中、「なお、ガンマ分布は次のように表される場合も多いです。」の定義中の「r」は「λ」でしょうか?(念のため)
ガンマ分布の2つの定義で、尺度母数の設定が、r=1/θになっているから、「ランダムな出来事が 1 回起こるまでの期間を 1/λ という逆数で表す」のでしょうかね。定義が2通りの表現があるのが、ややこしいですね。
大変勉強になりました。有り難うございました。